Степень с целым показателем и её свойства
| Формула | Правило | Пример |
| ап=а∙а∙а∙∙∙а
Если а ≠ 0 и n – целое отрицательное число, то
| Степенью числа а с натуральным показателем n 1 называется произведение n множителей, каждый из которых равен а.
Переход от отрицательного показателя к положительному. | 2 3 = 2· 2· 2 = 8; 54 = 625;
|
| Свойства степени | ||
|
| При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней складываются. |
25 · 2 – 7 = 25 +(- 7)=2 – 2 = |
|
| При делении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней вычитаются. |
х – 2: х – 4= х -2 – (- 4) = х – 2 + 4 = х2 |
|
| При возведении степени в степень основание остается прежним, а показатели степеней перемножаются. | (b2) – 3=b – 6 ; (2 – 3) – 2 = 26 = 64 |
|
| При возведении в степень произведения в эту степень возводится каждый множитель. |
|
|
| При возведении в степень дроби в эту степень возводится и числитель и знаменатель. |
|
| а ≠ 0, b ≠ 0 | Чтобы возвести дробь в степень с отрицательным показателем, надо дробь «перевернуть», а показатель степени изменить на противоположный. | |
| а1 = а | Любое число в нулевой степени равно 1.
Степенью числа а с показателем 1 называется само число а. |
|
Примеры: Упростить выражение:
-
1,5 ab – 3 · 6 a – 2b = 1,5 · 6 a· a – 2 · b – 3· b = 9a – 1 b – 2 ;
-
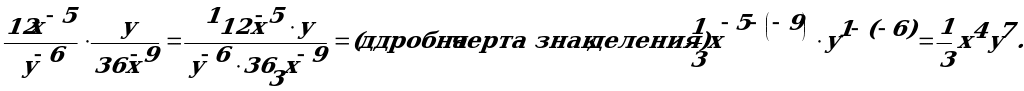



 Получите свидетельство
Получите свидетельство Вход
Вход



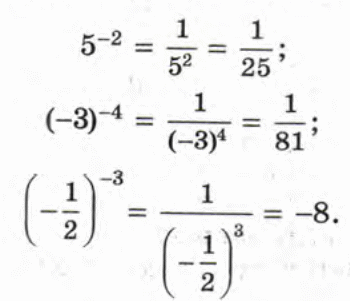
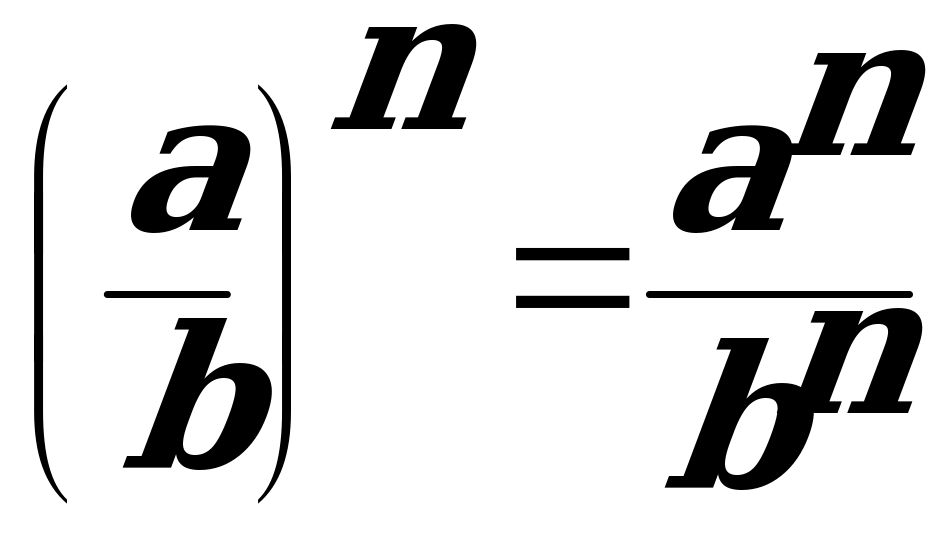 , b≠0
, b≠0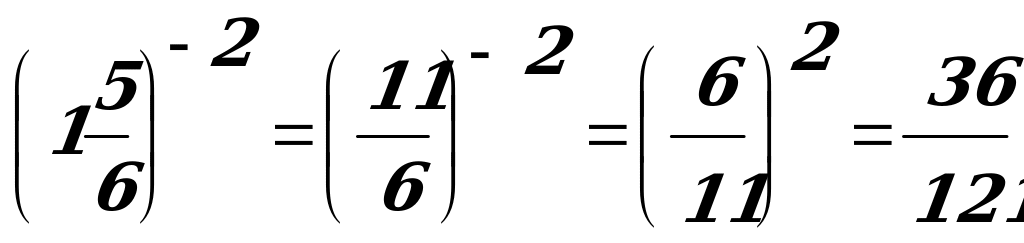
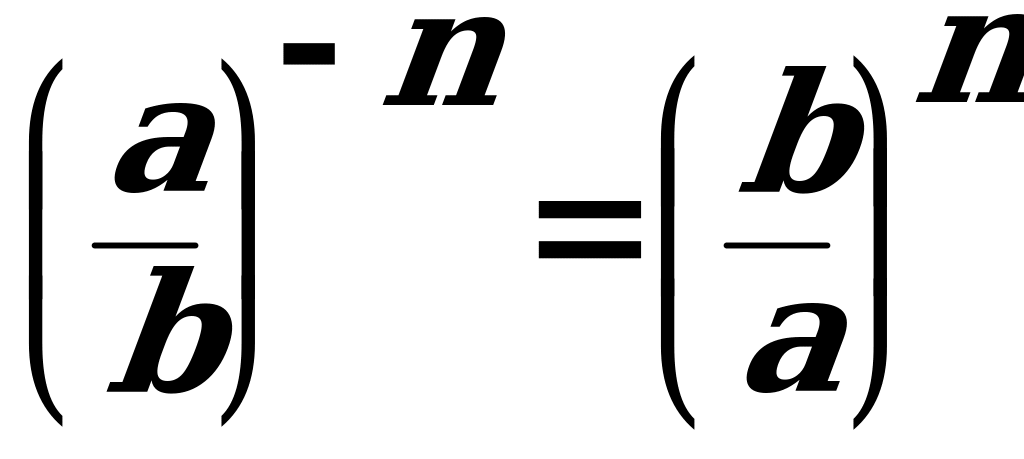









 Степень с целым показателем и её свойства (226 KB)
Степень с целым показателем и её свойства (226 KB)
 0
0 78
78 0
0 Нравится
0
Нравится
0




