Цель:
Закрепить полученные знания о степени с целым отрицательным и нулевым показателем.
Задачи:
- повторить понятие и свойства степени с целым показателем;
- развивать умение применять свойства степени с целым показателем в вычислениях и преобразованиях;
- развивать умения анализировать, рассуждать, сравнивать, делать выводы, осмысливать материал;
- развивать познавательный интерес учащихся к предмету, к истории математики.
Ход урока:
1) Организационный момент.
Здравствуйте, садитесь.
- На прошлом уроке мы познакомились со степенью с целым показателем, и свойствами таких. Сегодня мы научимся применять эти свойства в вычислениях и преобразованиях.
- Были ли трудности при выполнении домашней работы?
- Нет.
2) Актуализация знаний. Устные упражнения.
- Дайте определение степени с целым отрицательным показателем.
- Дайте определение степени с целым отрицат. показателем.
- Перечислите свойства степеней с целым показателем.
- Все свойства степени с натуральным показателем справедливы и для степени с любым целым показателем.
a n · a m = a n + m
a n : a m = a n - m
(a m) n = a m · n
(a · b)n = an · b n.
- Представьте выражение в виде степени с целым отрицательным показателем:
5-2; Х-10; 3-9; а-1
- Представьте в виде дроби...
- Представьте выражение в виде одночлена:
х-1; х-9; а7; b5; 1; 10; 1/16х3у-2
3) Работа по теме урока.
- Запишите в тетрадях число, классная работа.
Мы начнём нашу работу с №70 (2,4) и №71 (2,4), которые выполним с вами совместно, с объяснениями, пользуясь свойствами степени.
- Каким свойством степени пользовались при выполнении №70?
- При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
- Каким свойством степени пользовались при выполнении №71?
- При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются.
- Каким свойством степени пользовались при выполнении №72?
- При возведении степени в степень основание остается прежним, а показатели степеней перемножаются.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



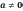
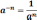

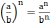

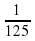 ;
; 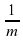 ;
; 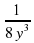 ;
; 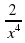
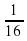 х3у-2
х3у-2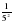 ;
; 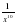 ;
; 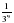 ;
; 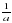 .
.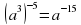
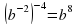
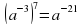
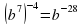
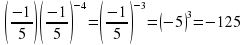









 Конспект урока по математике "Степень с целым показателем" (97.05 КB)
Конспект урока по математике "Степень с целым показателем" (97.05 КB)
 0
0 2609
2609 459
459 Нравится
0
Нравится
0


