Получите свидетельство
Вход
Логарифмическая функция
Цели урока:
- Образовательные - познакомить учащихся с логарифмической функцией, её основными свойствами, графиком; показать использование свойств, потребность к самообразованию, способствовать развитию творческой деятельности учлогарифмической функции при решении заданий.
- Развивающие – развивать математическую речь учащихсяащихся.
- Воспитательные - воспитывать познавательную активность, чувства ответственности, взаимоподдержки, уверенности в себе; воспитывать культуру общения.
Джон Непер
В области математики Джон Непер известен как изобретатель системы логарифмов, основанной на установлении соответствия между арифметической и геометрической числовыми прогрессиями. В «Описании удивительной таблицы логарифмов» он опубликовал первую таблицу логарифмов (ему же принадлежит и сам термин «логарифм»), но не указал, каким способом она вычислена. Объяснение было дано в другом его сочинении «Построение удивительной таблицы логарифмов», вышедшем в 1619, уже после смерти Непера. Таблицы логарифмов, насущно необходимые астрономам, нашли немедленное применение.
0 и а ≠ 1), называют логарифмической функцией с основанием а " width="640"
Определение логарифмической функции
Функцию, заданную формулой
y = log a x (где а 0 и а ≠ 1),
называют логарифмической функцией с основанием а
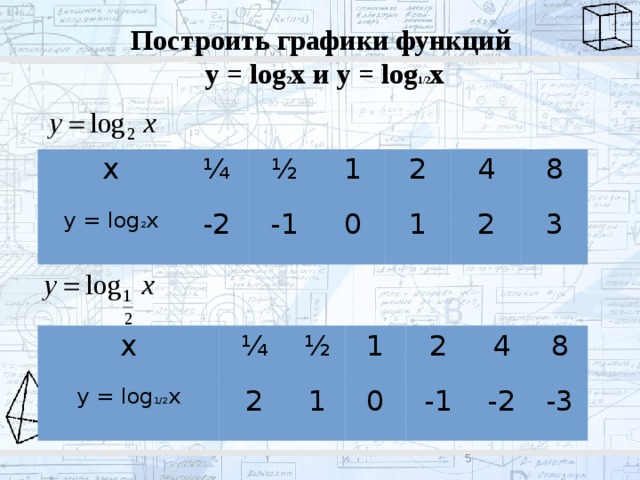
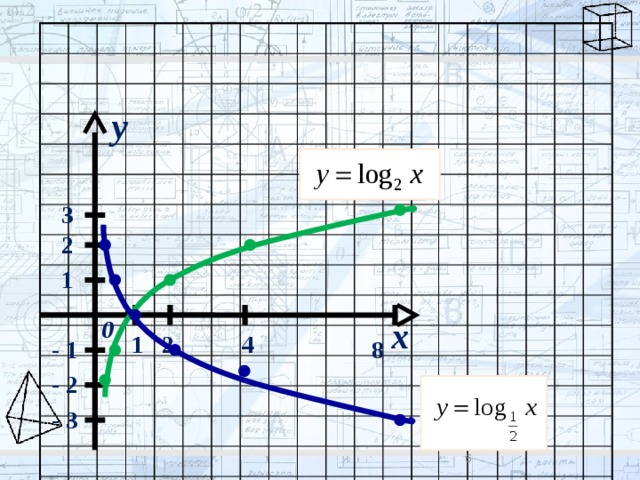
Построить графики функций
y = log 2 x и y = log 1/2 x
x
¼
y = log 2 x
½
-2
1
-1
2
0
4
1
8
2
3
x
y = log 1/2 x
¼
2
½
1
1
2
0
-1
4
8
-2
-3
y
3
2
1
0
x
4
1
2
- 1
8
- 2
- 3
1. у 1. D(f) =(0;+∞) 2. E(f) =R 3. Функция является ни четной, ни нечетной 4. Проходит через точку (1;0) 5. Промежутки знакопостоянства: у 0 при x € (1; +∞) у 6. Функция возрастает при x € (0; +∞). 7. Функция непрерывна. х 1 " width="640"
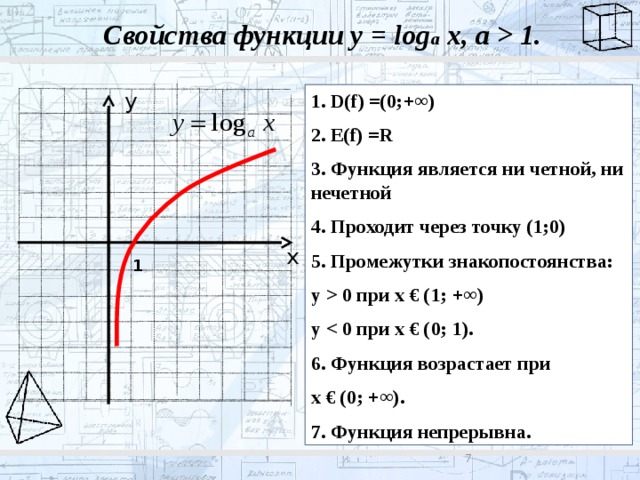
Свойства функции у = log a x, a 1.
у
1. D(f) =(0;+∞)
2. E(f) =R
3. Функция является ни четной, ни нечетной
4. Проходит через точку (1;0)
5. Промежутки знакопостоянства:
у 0 при x € (1; +∞)
у
6. Функция возрастает при
x € (0; +∞).
7. Функция непрерывна.
х
1
0 при x € (0; 1) у 6. Функция убывает при x € (0; +∞). 7. Функция непрерывна. х 1 7 " width="640"
Свойства функции у = log a x, 0
у
1. D (f) =(0;+∞)
2. E (f) =R
3. Функция является ни четной, ни нечетной
4. Проходит через точку (1;0)
5. Промежутки знакопостоянства:
у 0 при x € (0; 1)
у
6. Функция убывает при
x € (0; +∞).
7. Функция непрерывна.
х
1
7
Леонард Эйлер
Идеальный математик 18 века - так часто называют Эйлера. Он родился в маленькой тихой Швейцарии. В 1725 году переехал в Россию. Поначалу Эйлер расшифровывал дипломатические депеши, обучал молодых моряков высшей математике и астрономии, составлял таблицы для артиллерийской стрельбы и таблицы движения Луны. В 26 лет Эйлер был избран российским академиком, но через 8 лет он переехал из Петербурга в Берлин. Там "король математиков" работал с 1741 по 1766 год; потом он покинул Берлин и вернулся в Россию. Современное определение показательной, логарифмической и тригонометрических функций – заслуга Эйлера, так же как и их символика.
8
Определите, какие из перечисленных ниже функций являются возрастающими, а какие убывающими:
1) y = log 3 x;
2) y = log 2 x;
3) y = log 0,2 x;
4) y = log 0,5 (2x+5);
5) y = log 3 (x+2)
8
физкультминутка
8
8
Учебник стр 156. № 5.28 Учебник стр 156. № 5.30
8
Используя свойства
логарифмической функции, сравнить:
а) lоg 2 3 и log 2 5;
б) log 2 1/3 и log 2 1/5;
в)log 1/2 3 и log 1/2 5;
г)log 1/2 1/3 и log 1/2 1/5.
8
Блиц - опрос
1. Область определения логарифмической функции – вся числовая прямая, а область значений этой функции – промежуток (0, + ∞).
2. Монотонность логарифмической функции зависит от основания логарифма.
3. Не каждый график логарифмической функции проходит через точку с координатами (1; 0).
4. Логарифмическая функция является ни чётной, ни нечётной.
5. Логарифмическая функция непрерывна.
8
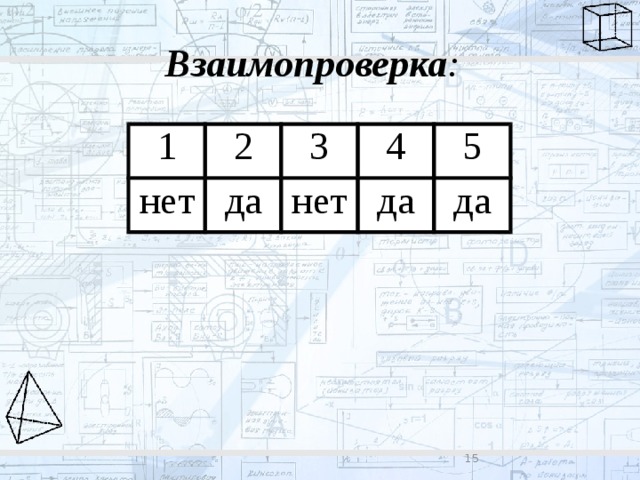
Взаимопроверка :
1
2
нет
3
да
4
нет
5
да
да
8
Домашнее задание
- Изучить п. 5.3.
2. Выполнить:
№ 5.31 ; 5.29
№ 5.35 (а), 5.36(а).
Доп. 5.35(б,в) , 5.36 ( ж)
Рефлексия
Вы считаете, что урок прошел плодотворно, с пользой.
Вы научились и можете помочь другим.
Я доволен
Вы считаете, что научились, но вам еще нужна помощь.
собой!
Я вполне
Вы считаете, что было трудно на уроке.
доволен
Мне нужна
собой!
помощь!
Спасибо за внимание!
Презентация "Логарифмическая функция" (1.52 MB)
0
1918
613
Нравится
0
