Презентация по матемтаике "Признаки возрастания и убывания функции"

Цели и задачи урока.

Образовательные:

закрепить навык нахождения производной, расширить и углубить знания по данной теме,

организовать деятельность учащихся по применению условий возрастания и убывания функции к нахождению промежутков монотонности функции,

применить знание производной для нахождения промежутков возрастания и убывания функции.

Развивающие:

развитие логического мышления учащихся, развитие памяти, внимания, монологической речи, умения рассуждать, выделять главное, самостоятельно приобретать знания, навыки и применять их на практике,

развитие умения давать объективную самооценку,

научить применять знакомые формулы в измененных условиях,

расширить кругозор сведениями из истории математики.

Воспитательные:

воспитание уважительного отношения к одноклассникам,

формирование самостоятельности,

развитие эстетического вкуса учащихся, аккуратности, внимательности, создание успеха,

воспитание интереса к математике.

Тип урока: урок формирования новых знаний, умений, навыков.

Форма проведения урока: проблемный урок.

Методы: наглядный, словесный, графический, условно - символический, исследовательский.

Оборудование:

интерактивная доска,

презентация «Возрастание и убывание функции»,

задания с тестами.

План урока:

Организационный момент.

Проверка домашнего задания. Создание проблемной ситуации

Изучение нового материала.

Закрепление нового материала. Организация коллективной работы.

Проверочная работа. Тест с оценкой.

Работа с последующей проверкой.

Первичный тест - контроль.

Ход урока:

Организационный момент.

  Взаимное приветствие учителя и учащихся, фиксация отсутствующих, проверка готовности учащихся к уроку.

Вступительное слово:

Она используется для нахождения таких характеристик, как сила, импульс, кинетическая энергия, мощность, линейная плотность. С ее помощью можно найти заряд, работу, массу тонкого стержня, теплоту. Можно вычислить приближенное значение функции, угол наклона между касательной и положительным направлением оси ох. Найти скорость и скорость изменение скорости. Исследовать свойства функции, определять критические точки, наибольшее, наименьшее значение функции.

 О чем идет речь?

О производной.

Весь материал – смотрите документ.

Признаки возрастания и убывания функций 10 класс

Учитель математики

Калита Н.А.

0 на (-∞;0) U (4;+∞) у 0 на (0;4) ? ? ? Дальше " width="640"

Домашнее задание: Исследовать свойства функции: у=х 4 -4х 3

1.

Область определения

2.

Четность, нечетность

3.

Нули функции

4.

Знакопостоянство

5.

Монотонность

6.

Экстремумы

7

Область значения

R

Не является четной, не является нечетной

(0;0) и (0;4)

у 0 на (-∞;0) U (4;+∞)

у 0 на (0;4)

?

?

?

Дальше

Область определения-те значения, которые может принимать аргумент

Область определения данной функции- множество всех действительных чисел, т.к. задана в виде целой рациональной функции (многочлена)

Четность , нечетность

Функция четная- если противоположным значениям аргумента соответствуют одни и те же значения функции.

f (-х)= f (х)

Функция нечетная- если противоположным значениям аргумента соответствуют противоположные значения функции.

f (-х)=- f (х)

у=х 4 -4х 3

у(-х)=(-х) 4 -4(-х) 3 = х 4 +4х 3 значит . . .

Нули функции

Нулями функции называют значения аргумента х при которых значение функции у равно нулю.

у=0; х 4 -4х 3 =0;

х 3 (х-4)=0;

х 1 =0 и х 2 =4

(0;0) и (4;0) – точки пересечения графика с осью ох

0; х 4- 4х 3 0 у 0; х 4 -4х 3 0 х 3 (х-4) 0 х 3 (х-4) 0 0 4 + + - " width="640"

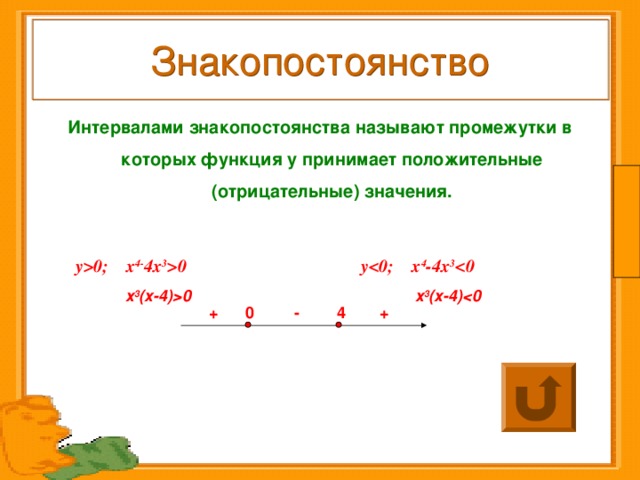
Знакопостоянство

Интервалами знакопостоянства называют промежутки в которых функция y принимает положительные (отрицательные) значения.

у 0; х 4- 4х 3 0 у 0; х 4 -4х 3 0

х 3 (х-4) 0 х 3 (х-4) 0

0

4

+

+

-

x 2 ) , выполнено неравенство y (x 2 ) y (x 1 ) Функция y убывает на множестве P , если для любых x 1 и x 2 из множества P ( x 1 x 2 ) , выполнено неравенство y (x 2 ) 1 ) " width="640"

Монотонность

• Функция y возрастает на множестве P , если для любых x 1 и x 2 из множества P

( x 1 x 2 ) , выполнено неравенство

y (x 2 ) y (x 1 )

• Функция y убывает на множестве P , если для любых x 1 и x 2 из множества P

( x 1 x 2 ) , выполнено неравенство

y (x 2 ) 1 )

Экстремумы

Точка x 0 называется точкой минимума функции y , если для всех x из некоторой окрестности x 0 выполнено неравенство

у(х) ≥у(х 0 )

Точка x 0 называется точкой максимума функции y , если для всех x из некоторой окрестности x 0 выполнено неравенство

у(х) ≤ у(х 0 )

Область значения

Те значения которые принимает функция

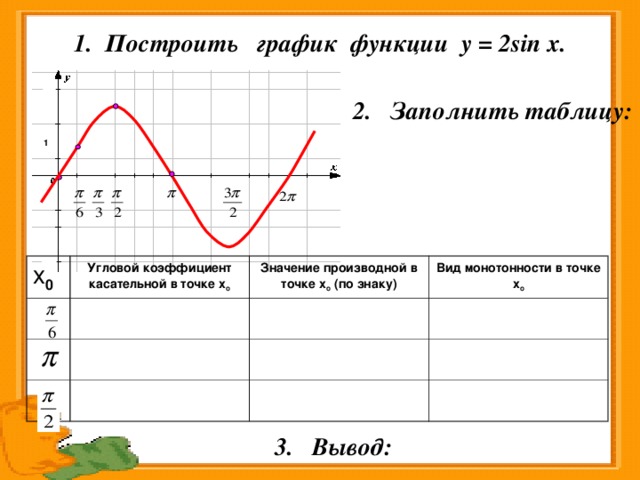
1. Построить график функции y = 2 sin x .

2. Заполнить таблицу:

1

х 0

Угловой коэффициент касательной в точке х о

Значение производной в точке х о (по знаку)

Вид монотонности в точке х о

3. Вывод:

Вывод:

Если функция возрастает на промежутке и имеет на нем производную, то производная положительна;

Если функция убывает на промежутке и имеет на нем производную, то производная отрицательна.

0, то и у ' 0. " width="640"

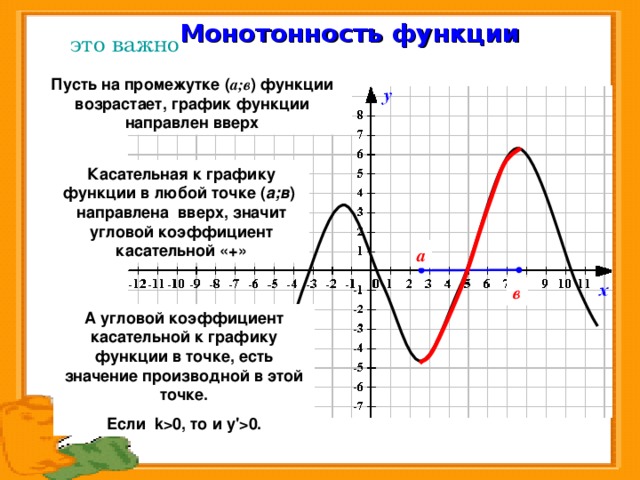
Монотонность функции

это важно

Пусть на промежутке ( а;в ) функции возрастает, график функции направлен вверх

Касательная к графику функции в любой точке ( а;в ) направлена вверх, значит угловой коэффициент касательной «+»

а

в

А угловой коэффициент касательной к графику функции в точке, есть значение производной в этой точке.

Если k 0, то и у ' 0.

0 в каждой точке интервала ( а;в ), то функция f (х) возрастает на ( а;в ). " width="640"

Т.о.

Если f‘ (х) 0 в каждой точке интервала ( а;в ),

то функция f (х) возрастает на ( а;в ).

Аналогично

Если f‘ (х) 0 в каждой точке интервала ( а;в ),

то функция f (х) убывает на ( а;в ).

0, то функция возрастает на интервале (а;в). Если функция f (х) дифференцируема на интервале (а;в ) и f‘ (х) 0, то функция убывает на интервале (а;в). " width="640"

Данные свойства называют достаточные признаки возрастания, убывания функции.

Если функция f (х) дифференцируема на интервале (а;в ) и f‘ (х) 0, то функция возрастает на интервале (а;в).

Если функция f (х) дифференцируема на интервале (а;в ) и f‘ (х) 0, то функция убывает на интервале (а;в).

Алгоритм исследования на монотонность:

• Найдем о.о. производной функции.
• Найдем производную функцию.
• Найдем нули производной.
• Методом интервалов определим знаки производной на каждом промежутке.
• Используя достаточный признак возрастания (убывания) делаем вывод.

0, x ϵ (-∞; 1 ) и (3; + ∞ ) f ´(x) 0, х ϵ (1; 3) f ´(x) + - + х 1 3 Вывод: Функция f(x) = x³ - 6x² + 9x – 1 Возрастает на ( -∞; 1 ] и [ 3; + ∞ ) Убывает на [ 1; 3 ] " width="640"

Пример:

Исследовать функцию на монотонность : f(x) = x³ - 6x² + 9x – 1

Решение:

1. Данная функция определена на R .

Найдем производную данной функции:

f ´(x) = 3x² - 12x + 9

2. Найдем нули производной:

f ´(x) = 0, 3x² - 12x + 9 = 0

x² - 4x + 3 = 0

x = 1 и х = 3

3. Определим знак производной на интервалах:

f ´(x) 0, x ϵ (-∞; 1 ) и (3; + ∞ )

f ´(x) 0, х ϵ (1; 3)

f ´(x)

+

-

+

х

1

3

Вывод: Функция f(x) = x³ - 6x² + 9x – 1

Возрастает на ( -∞; 1 ] и [ 3; + ∞ )

Убывает на [ 1; 3 ]

№ 1 : Определите на каких промежутках функция у=х 3 -3х+2 возрастает, а на каких убывает.

Дальше

№ 2 :

Доказать, что функция y = cos 3 x - 4x убывает на всей числовой прямой

Дальше

№ 3 : Является ли данная функция возрастающей?

Дальше

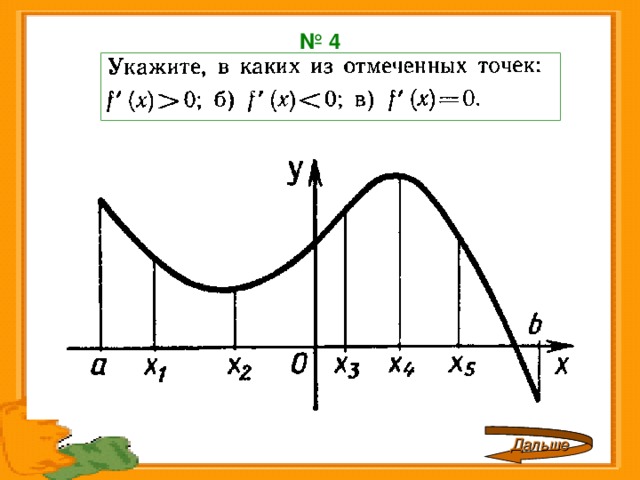
№ 4

Дальше

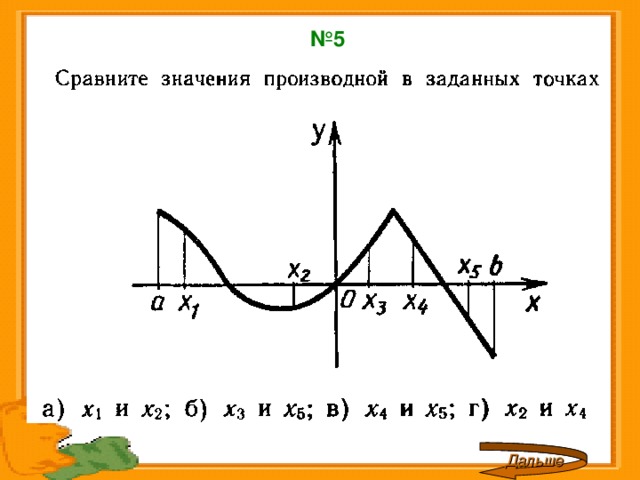
№ 5

Дальше

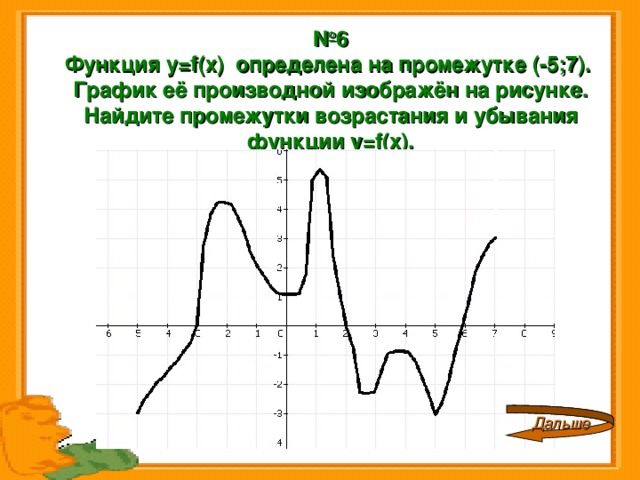
№ 6 Функция y = f ( x ) определена на промежутке (-5;7). График её производной изображён на рисунке. Найдите промежутки возрастания и убывания функции y=f(x).

Дальше

ИССЛЕДОВАНИЕ МОНОТОННОСТИ ПО ГРАФИКУ

Тест состоит из 5 вопросов.

К каждому вопросу предложено 4 ответа, один из них верный. Каждый верный ответ приносит вам 1 балл, неверный 0 баллов.

Желаю удачи!

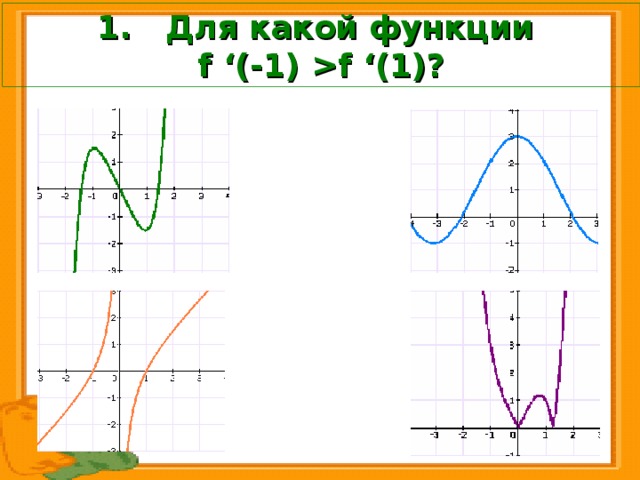f ‘ (1) ? " width="640"

• Для какой функции

f ‘ (-1) f ‘ (1) ?

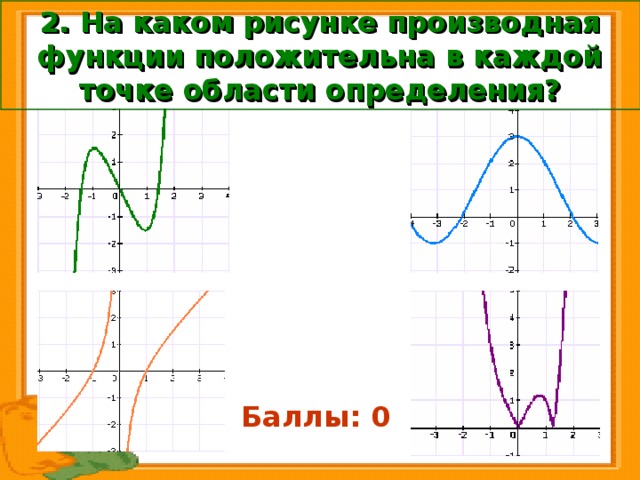
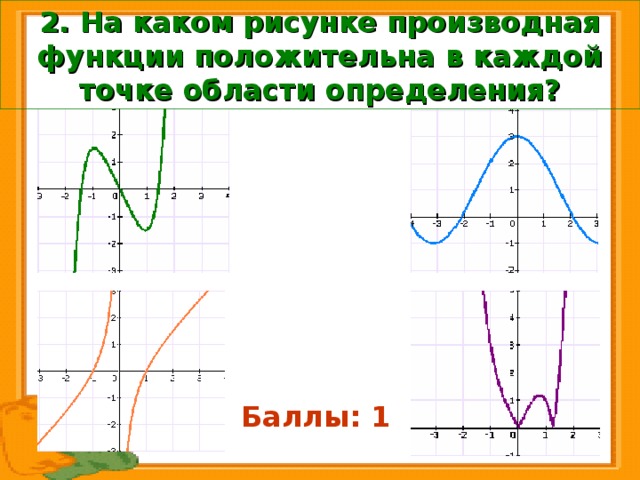
2. На каком рисунке производная функции положительна в каждой точке области определения?

Баллы: 0

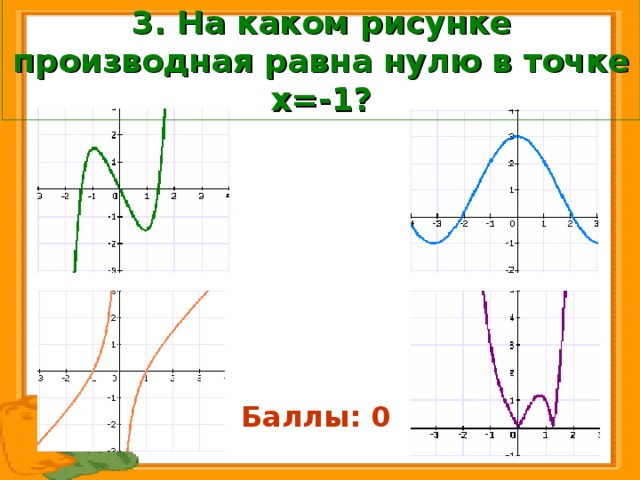
2. На каком рисунке производная функции положительна в каждой точке области определения?

Баллы: 1

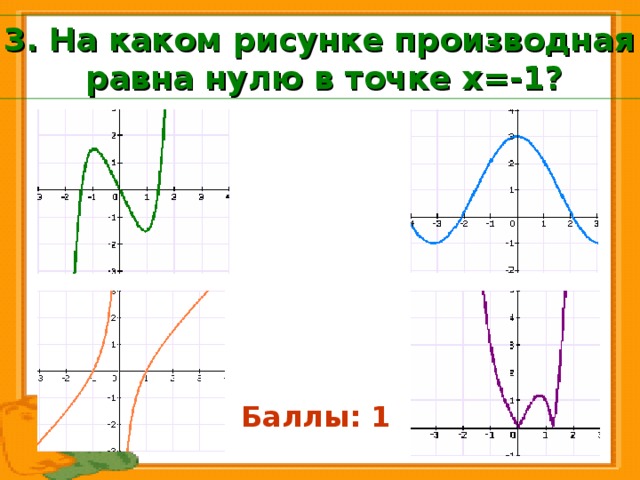
3. На каком рисунке производная равна нулю в точке х=-1?

Баллы: 0

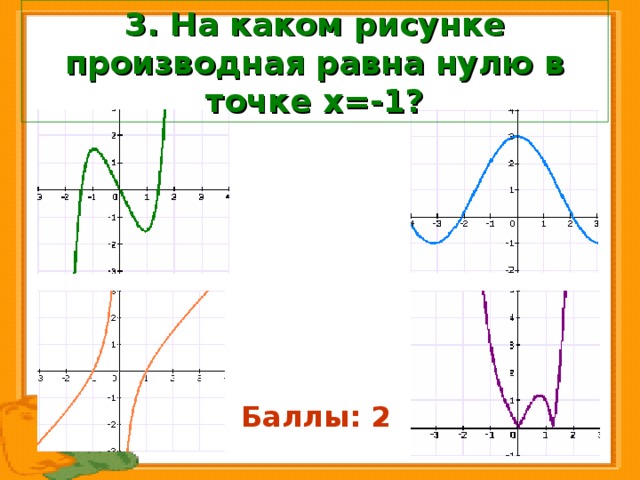
3. На каком рисунке производная

равна нулю в точке х=-1?

Баллы: 1

3. На каком рисунке производная равна нулю в точке х=-1?

Баллы: 2

4. На каком рисунке производная функция отрицательна на [- 1 ; 1 ] ?

Баллы: 0

4. На каком рисунке производная функции отрицательна на [- 1 ; 1 ] ?

Баллы: 1

4. На каком рисунке производная функции отрицательна на [- 1 ; 1 ] ?

Баллы: 2

4. На каком рисунке производная функция отрицательна на [- 1 ; 1 ] ?

Баллы: 3

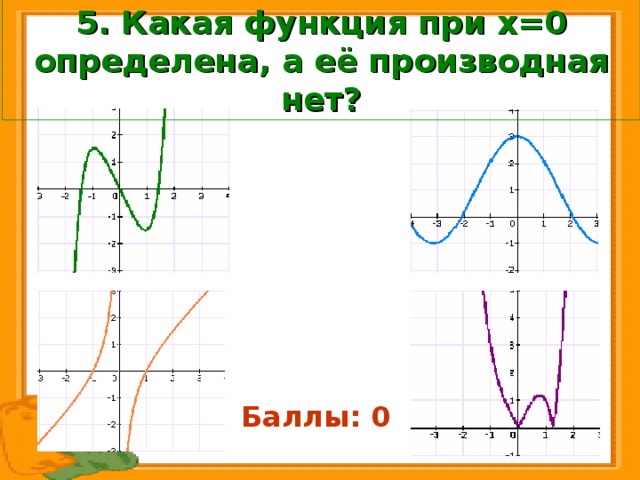
5. Какая функция при х=0 определена, а её производная нет?

Баллы: 0

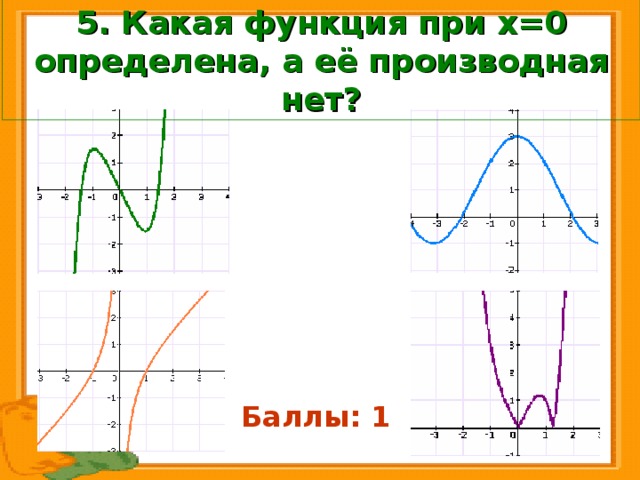
5. Какая функция при х=0 определена, а её производная нет?

Баллы: 1

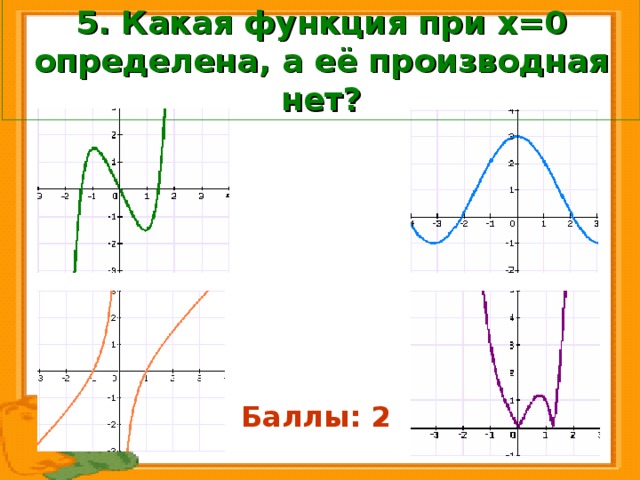
5. Какая функция при х=0 определена, а её производная нет?

Баллы: 2

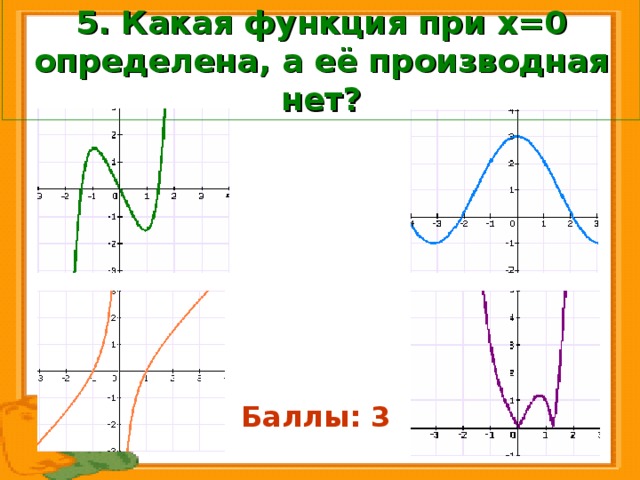
5. Какая функция при х=0 определена, а её производная нет?

Баллы: 3

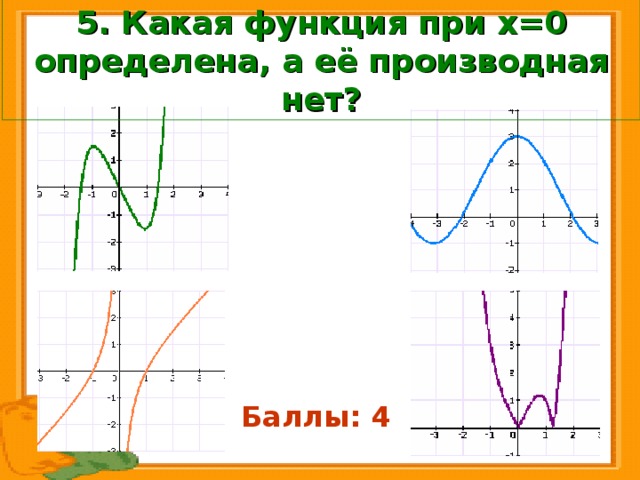
5. Какая функция при х=0 определена, а её производная нет?

Баллы: 4

Блиц-тестирование окончено

0, х ϵ ( 3; + ∞ ) 4. Вывод: Функция возрастает на [ 3; +∞) и убывает на (-∞; 3 ] . + - - 3 0 " width="640"

Используя изученные признаки определим промежутки монотонности заданной в домашнем задании, функции у=х 4 -4х 3

Решение:

1. Найдем производную данной функции: f ´(x) = 4 x 3 - 12x 2

Данная функция определена на R

2. Найдем нули производной

f ´(x) = 0, 4 x 3 - 12x 2 = 0

4 x² (х-3) = 0

x = 0 и х = 3

3. Определим знак производной на интервалах:

f ´(x) 0, x ϵ (-∞; 3 )

f ´(x) 0, х ϵ ( 3; + ∞ )

4. Вывод: Функция возрастает на [ 3; +∞) и убывает на (-∞; 3 ] .

+

-

-

3

0

Домашнее задание:

• Признаки возрастания и убывания функции
• № 260
• № 261