Урок обобщения и систематизации знаний
Тема: «Преобразование тригонометрических выражений».
Преподаватель: Ромашкина О.В
Цель:
Систематизировать, расширить и углубить знания, умения при применении различных формул тригонометрии для преобразования тригонометрических выражений.
ЗАДАЧИ :
- Повторить определение синуса, косинуса, тангенса, котангенса числа α;
- Повторить основные тригонометрическое тождество, формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом; формулы двойного угла, формулы сложения;
- Закрепить умение применять полученные знания для преобразования тригонометрических выражений.
“ Три пути ведут к знанию: путь РАЗМЫШЛЕНИЯ – это путь самый благородный, путь ПОДРАЖАНИЯ – это путь самый легкий и путь ОПЫТА – это путь самый горький”.
– Конфуций-
ПОСТАВЬТЕ ПЕРЕД СОБОЙ ЦЕЛЬ.
«Сегодня на уроке я хочу узнать …»
«Сегодня на уроке я хочу уточнить …»
«Сегодня на уроке я хочу понять …»
«Сегодня на уроке я хочу выяснить …»
Что такое
тригонометрия?
Где применяются тригонометрические функции?
Что такое тригонометрия???
Тригонометрия (от греч. trigonon – треугольник, metro – метрия) – микрораздел математики , в котором изучаются зависимости между величинами углов и длинами сторон треугольников, а также алгебраические тождества тригонометрических функций.
Истоки тригонометрии берут начало в древнем Египте, Вавилонии и долине Инда более 3000 лет назад.
Слово тригонометрия впервые встречается в 1505 году в заглавии книги немецкого математика Питискуса.
Где применяется тригонометрия?
Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей. Следует отметить применение в таких областях как: физика, природа, биология, музыка, медицина и многие другие.
Тригонометрия в физике
В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений, например:
Механические колебания
Гармонические колебания
Теория радуги
Радуга возникает из-за того, что солнечный свет испытывает преломление в капельках воды, взвешенных в воздухе по закону преломления:
sin α / sin β = n 1 / n 2
Тригонометрия в живой природе
- Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения.
- Также в биологии используется такое понятие как синус сонный, синус каротидный и венозный или пещеристый синус.
Связь движения рыб в воде с тригонометрическими функциями
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксиров точку на хвосте, а потом рассмотреть траекторию движения.
Y= tg x
Тригонометрия в медицине:
- Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца - комплексное алгебраически - тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
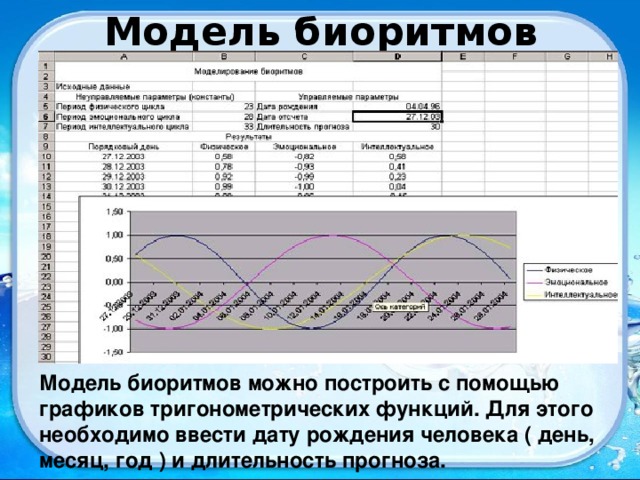
Модель биоритмов
Модель биоритмов можно построить с помощью графиков тригонометрических функций. Для этого необходимо ввести дату рождения человека ( день, месяц, год ) и длительность прогноза.
Тригонометрия прошла длинный путь развития. И теперь, мы можем с уверенностью сказать, что тригонометрия не зависит от других наук, а другие науки зависят от тригонометрии.
Упростить выражения :
- cos 2 α - sin 2 α
- 1
- cos α cos β – sin α sinβ
- 1/ cos 2 α
- sin α cos β - cos α sin β
- cos α
- - sin α
8. - cos α
- Cos2α =
- tg α ctgα =
- cos (α + β)=
- 1+ tg 2 α=
- sin (α - β)=
- cos ( - α)=
- sin(2π + α)=
- cos (π - α)=
- 2 sinα cosα
- 1
- sin α cos β + cos α sinβ
- 1/ sin 2 α
- cos α cos β + sin α sin β
- - tg α
- - sin α
8. cos α
- Sin 2α =
- Sin 2 x+ cos 2 x =
- sin (α + β)=
4. 1+ c tg 2 α=
5. cos (α - β) =
6. tg ( - α) =
7. sin(π + α)=
8. cos (2π - α)=
Выставление оценок:
8 правильных – оценка « 5 »
6-7 правильных – оценка « 4 »
4-5 правильных – оценка « 3 »
Менее 4 правильных –оценка « 2 »
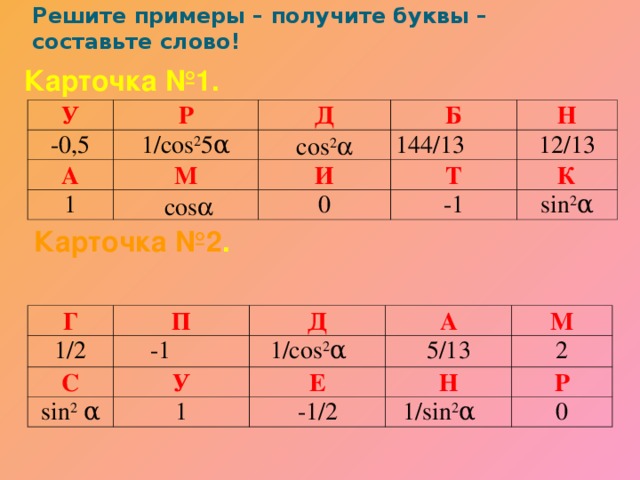
Решите примеры – получите буквы – составьте слово!
Карточка №1.
У
-0,5
Р
Д
А
1/cos 2 5α
1
М
Б
cos 2
И
144/13
cos
Н
12/13
Т
0
-1
К
sin 2 α
Карточка №2 .
Г
1/2
П
С
-1
Д
sin 2 α
1/cos 2 α
А
У
Е
1
М
5/13
Н
2
-1/2
1/sin 2 α
Р
0
- Градусное измерение углов возникло в Древнем Вавилоне задолго до новой эры. Слово « градус » происходит от латинского gradus (шаг, ступень).
- Другая единица измерения углов – радиан – введена совсем недавно. Первое издание, содержащее термин «радиан», появилось в 1873 году в Англии. Сам термин « радиан » происходит от латинского radius (спица, луч).
Угол в один радиан – это такой центральный угол, длина дуги которого равна радиусу окружности.
Упростите выражение:
Решение:
Вычислите:
Решение:
2
Самостоятельная работа.
« Сегодня на уроке я узнал …»
« Сегодня на уроке я повторил …»
« Сегодня на уроке мне удалось понять …»
« Сегодня на уроке я закрепил …»
«Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое».
Российский математик и механик, академик Петербургской АН М.В. Остроградский
Какую бы задачу вы ни решали, в конце вас ждет счастливая минута – радостное чувство успеха, укрепление веры в свои силы. Д. К. Фадеев
Получите свидетельство
Вход
Презентация по математике "Тригонометрические выражения" (8.86 MB)
0
1720
320
Нравится
0
