Презентация к уроку
«Тригонометрические уравнения»
Учитель математики высшей категории
Гараева Фарида Халитовна
Цели урока:
- Повторить понятия синус, косинус, тангенс и котангенс угла; свойства тригонометрических функций.
- Систематизировать, расширить и углубить знания, умения учащихся применять тригонометрические формулы и различные методы при решении тригонометрических уравнений.
- Формировать самоконтроль, взаимоконтроль, самоанализ.
- Продолжить учиться работать в команде.
- Нравственное воспитание учащихся, развитие коммуникативных умений, рефлексии, культуры и дисциплины умственного труда
Эпиграфом к нашему уроку я взяла слова Конфуция:
“ Три пути ведут к знанию: путь РАЗМЫШЛЕНИЯ – это путь самый благородный, путь ПОДРАЖАНИЯ – это путь самый легкий
и путь ОПЫТА – это путь самый горький”
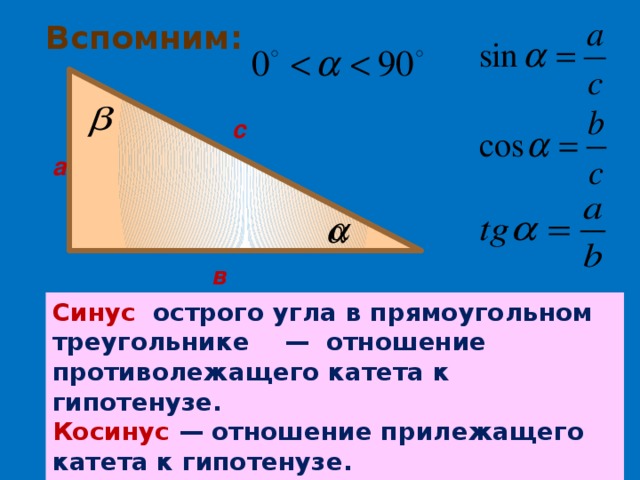
Вспомним:
с
а
в
Синус острого угла в прямоугольном треугольнике — отношение противолежащего катета к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к прилежащему.
В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось.
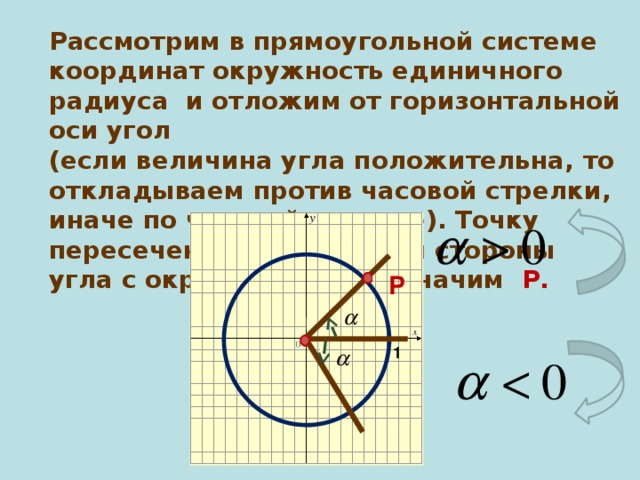
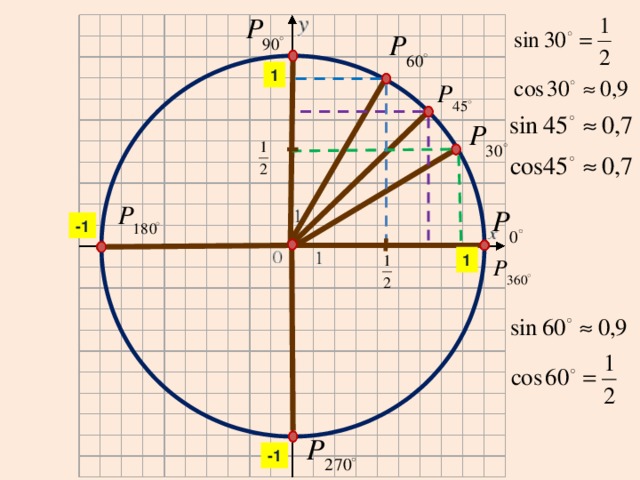
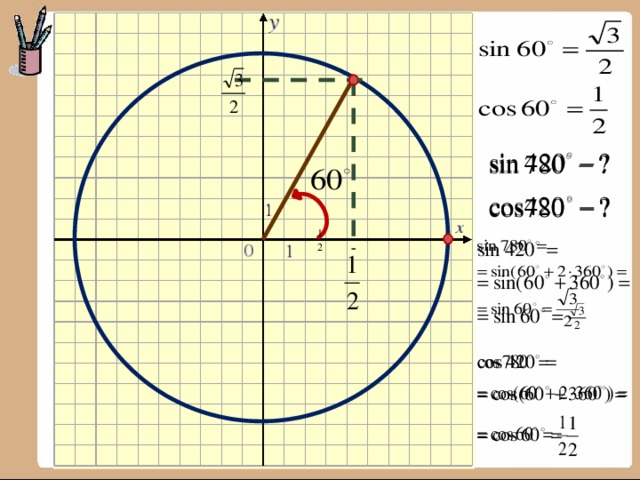
Рассмотрим в прямоугольной системе координат окружность единичного радиуса и отложим от горизонтальной оси угол
(если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим Р.
Р
1
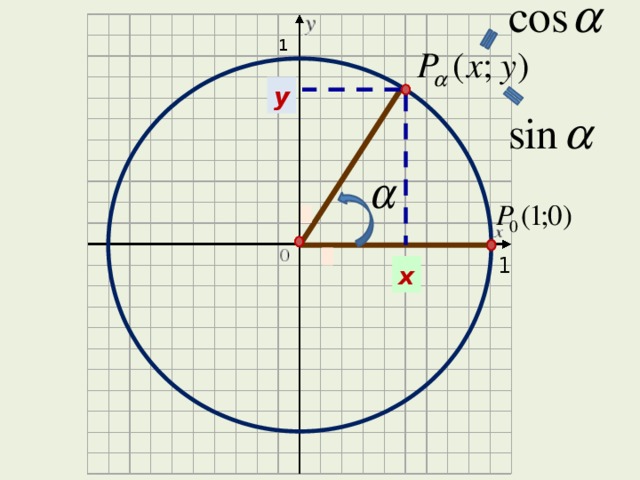
1
у
1
х
Синус угла определяется как ордината
точки
Косинус — абсцисса точки
Тангенс – отношение ординаты к абсциссе
точки
Котангенс – отношение абсциссы к ординате
точки
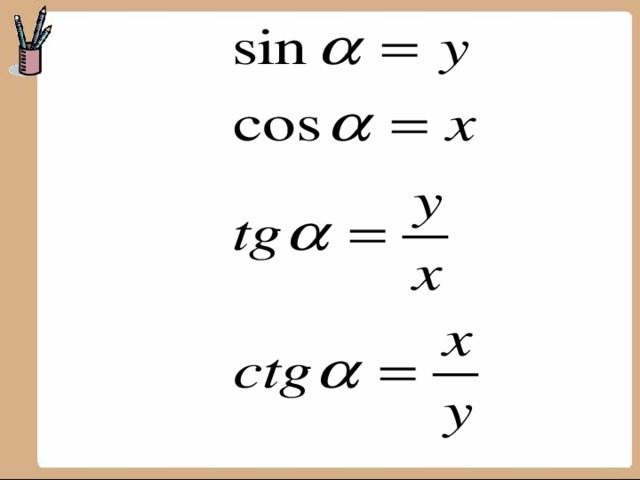
1
-1
1
-1
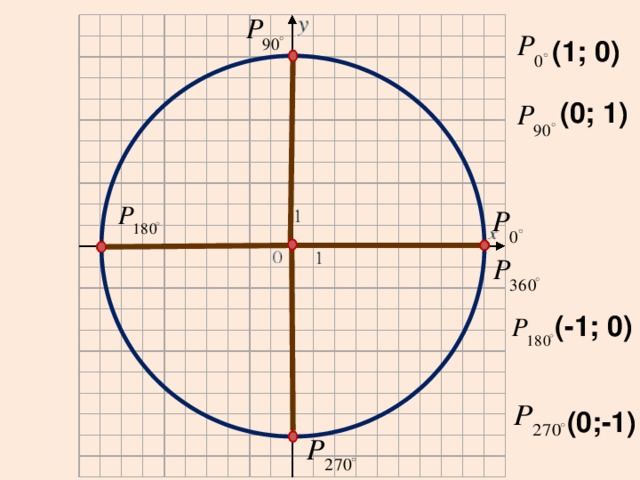
(1; 0)
(0; 1)
(-1; 0)
(0;-1)
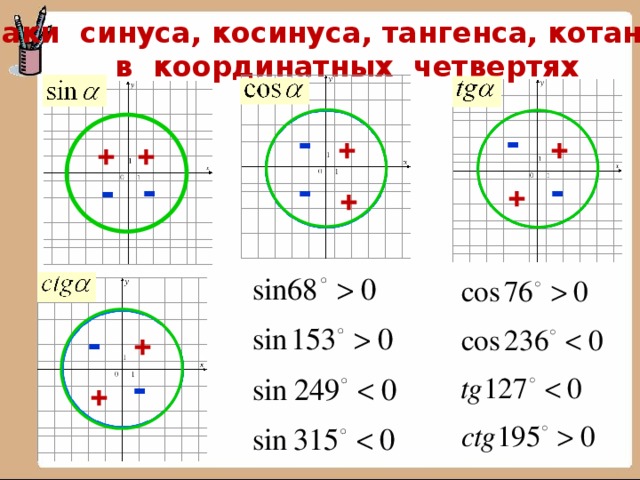
Знаки синуса, косинуса, тангенса, котангенса
в координатных четвертях
-
-
+
+
+
+
-
-
-
-
+
+
-
+
-
+
Четность, нечетность синуса, косинуса,
тангенса, котангенса
Нечетные функции
Четная функция
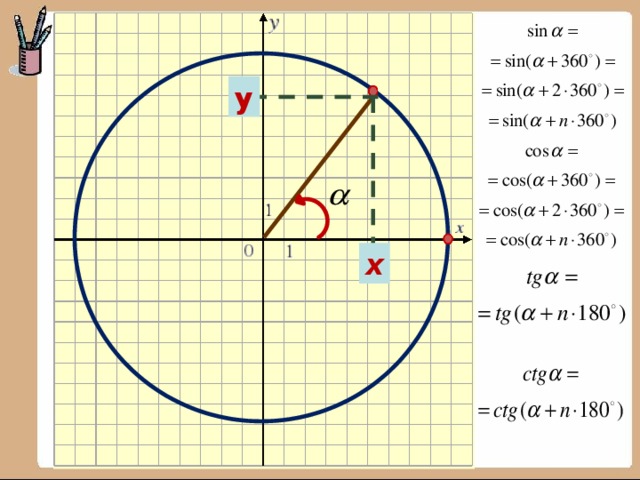
Периодичность тригонометрических
функций
При изменении угла на целое число оборотов
значения синуса, косинуса, тангенса, котангенса
не изменяются
у
х
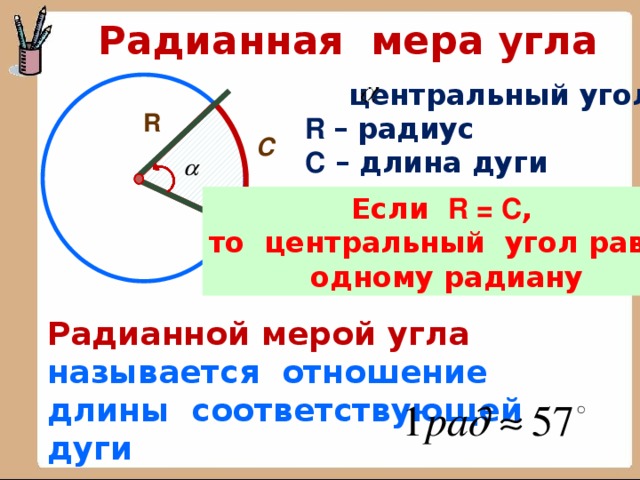
Радианная мера угла
центральный угол
R – радиус
С – длина дуги
R
С
Если R = C ,
то центральный угол равен
одному радиану
Радианной мерой угла называется отношение длины соответствующей дуги
к радиусу окружности
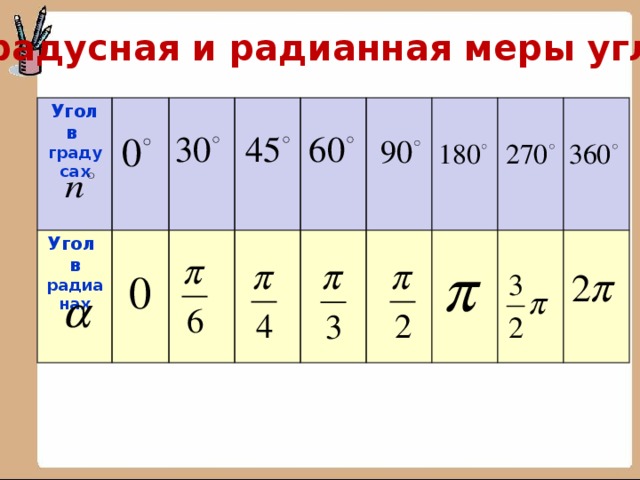
Градусная и радианная меры углов
Угол
в градусах
Угол
в
радианах
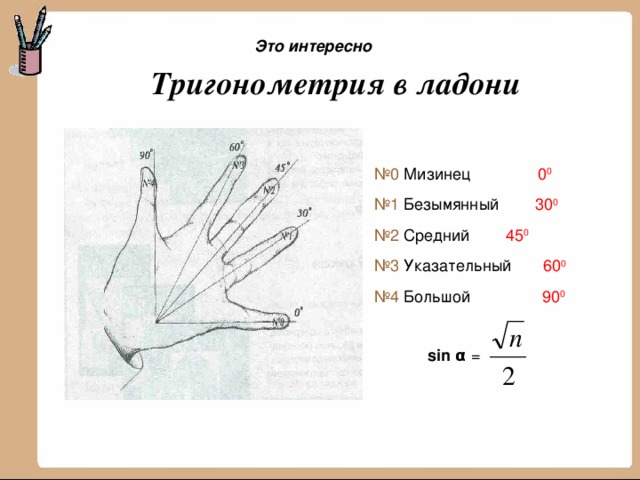
Это интересно
Тригонометрия в ладони
№ 0 Мизинец 0 0
№ 1 Безымянный 30 0
№ 2 Средний 45 0
№ 3 Указательный 60 0
№ 4 Большой 90 0
sin α =
Физкультминутка:
3
6
8
15
10
13
20
18
7
1
14
12
11
17
4
2
Блиц-опрос
- Синусом угла α называется _____ точки, полученной поворотом точки______ вокруг начала координат на угол α
- tg α =
- Косинусом угла α называется _____ точки, полученной поворотом точки______ вокруг начала координат на угол α
- ctg α=
- tg α∙ ctg α=
- sin 2 α +cos 2 α=
- 1+ tg 2 α=
- sin(-α)=
- tg (-α) =
- cos (α+ β)=
- sin (α- β)=
- sin 2α =
- tg (α+ β)=
- sin(π- α)=
- cos (π/2 + α)=
- sin(2π- α)=
- cos (-α)=
- ctg (-α) =
- cos (α- β)=
- sin (α+ β)=
- cos 2α =
10. tg 2α =
11. cos(π- α)=
- sin (π/2 + α)=
- cos(2π - α)=
Блиц-опрос
- Синусом угла α называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол α
- tg α = sin α / cos α
- Косинусом угла α называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол α
- ctg α= cos α / sin α
- tg α∙ ctg α = 1
- sin 2 α +cos 2 α = 1
- 1+ tg 2 α =
- sin(-α) = - sin α
- tg (-α) = -tg α
- cos (α+ β) = cos α cos β – sin α sinβ
- sin (α- β) = sin α cos β - cos α sin β
- sin 2α = 2sin α cos α
- tg (α+ β) =
- sin(π- α) =sin α
- cos (π/2 + α) = -sinα
- sin(2π- α)= - sin α
- cos (-α) = cos α
- ctg (-α) = -ctg α
- cos (α- β)=cos α cos β +sin α sinβ
- sin (α+ β)= sin α cos β + cos α sin β
- cos 2α =cos 2 α-sin 2 α
- tg 2α =
- cos(π- α)= - cos α
- sin (π/2 + α)= cos α
- cos(2π - α)= cos α
А.Эйнштейн говорил так «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».
Вот мы и займемся уравнениями…
Тригонометрические уравнения – уравнения, содержащие sin , cos, tg и ctg от неизвестного или от выражения, содержащего неизвестное.
Чтобы научиться решать тригонометрические уравнения, нужно уверенно решать простейшие тригонометрические уравнения.
Формулы корней простейших тригонометрических уравнений
1.cost = а , где | а| ≤ 1
3. tgt = а, а ЄR
2.sint = а, где | а |≤ 1
t = arctg а + πk‚ kЄZ
или
или
Частные случаи
Частные случаи
4. ctgt = а, а ЄR
1) cost=0
t = π/2+πk‚ kЄZ
1) sint=0
t = 0+πk‚ kЄZ
t = arcctg а + πk‚ kЄZ
2) sint=1
2) cost=1
t = π/2+2πk‚ kЄZ
t = 0+2πk‚ kЄZ
3) sint = - 1
3) cost = -1
t = - π/2+2πk‚ kЄZ
t = π+2πk‚ kЄZ
- Найдите корни уравнения: . В ответе запишите наибольший отрицательный корень.
- Решите уравнение . В ответе напишите наименьший положительный корень.
- Решите уравнение . В ответе напишите наименьший положительный корень.
Решение тригонометрических уравнений заданий ЕГЭ С1
1) Решите уравнение
cos 2x = 1 – cos (π /2 – x).
Укажите все корни уравнения, принадлежащие
промежутку [ -5π/2 ; - π ).
1 + 9 + 8 = 0.
tg² x tg x
Укажите все корни уравнения,
принадлежащие промежутку ( π/2 ; 3π/2 ).
3) Решите уравнение
4 sin² x + 2 sin x · cos x = 3.
тригонометрические уравнения
5.Однородные
1)Первой степени:
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно
не равны нулю, то разделим обе
части уравнения на cosx. Получим:
простое уравнение
a∙tgx + b = 0 или tgx = m
1. Простейшие уравнения и
уравнения , сводящиеся к
простейшим
2.Линейные уравнения вида
a∙sinx + b∙cosx = c
3. Уравнения, решаемые
разложением на множители
2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x.
Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.
6. Комбинированные уравнения
4.Сводимые к квадратным
a∙sin²x + b∙sinx + c=0
Пусть sinx = p, где |p| ≤1, тогда
a∙p² + b∙p + c = 0
Найти корни, вернуться к замене и
решить простые уравнения.
Домашнее задание
Спасибо за внимание!
Получите свидетельство
Вход
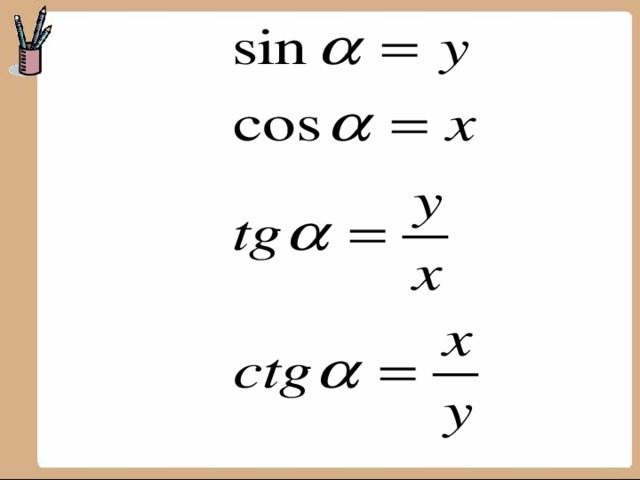
Презентация по математике "Тригонометрические уравнения" (0.48 MB)
0
1105
117
Нравится
0
