Презентация по математике "Тригонометрические уравнения и неравенства"

В связи с тем, что на изучение каждой темы из курса математики 10 - 11 классов дается только два занятия, то для успешного усвоения материала студентов 1 курса горнотехнического техникума мною была разработана презентация по теме: «Тригонометрические уравнения и неравенства».

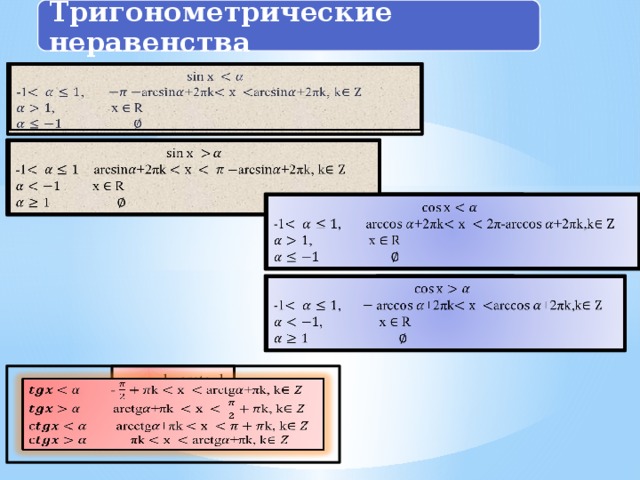
В презентации рассматриваются общие формулы решений простейших тригонометрических уравнений, когда значения тригонометрических функций принимают положительное и отрицательное значение. Также рассмотрены формулы для решения  тригонометрических неравенств, когда значения функций больше или меньше данного числа.

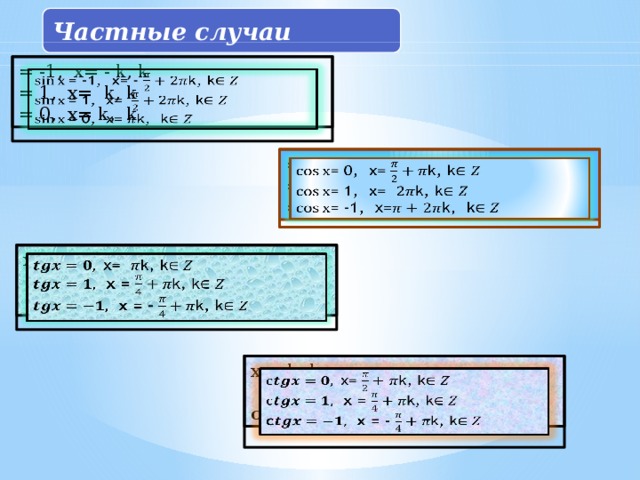
А также приведены формулы частного случая тригонометрических уравнений. В начале занятий приведена устная разминка на тему: «Нахождение значений обратных тригонометрических функций», с последующей проверкой, где студенты сразу смогут увидеть результат решения и самостоятельно оценить свои знания.

Даны 5 примеров с ответами основных видов тригонометрических уравнений: однородные тригонометрические уравнения 1 - й и 2 - й степени.

Тригонометрические уравнения и неравенста

Устная разминка

Вычисли и запиши в столбик

ответы в тетради:

Проверь ответы:

1. arcsin

2. arccos

3. arctg

-

4. arctg ( - )

-

5. arcsin (– )

π

6. arccos (-1)

7 arcсоs( - )

2

2

формулы для решения тригонометрических уравнений:

3. sinx = a , а [-1,1]

х=

1.сos x = a , а [-1,1]

k

х = ± arccos a + 2πk, k

(-1) ·arcsin a + πk, k

2.сos x = - a , а [-1,1]

х =± (π- arccos a) + 2πk, k

4. sinx = - a , а [-1,1]

х=

k+1

(-1) ·arcsin a + πk, k

5. tgx = a

х = arctg a +πk, k

7.сtgx = a

х=

arcctg a +πk, k

6. tgx = - a

х = -arctg a +πk, k

8.сtgx = - a

х=

(π - arcctg a) +πk,k

Реши уравнения базового уровня

Проверь ответы:

• х= ±π/6+2πk.
• х= (-1) · (-π/6) +πn/2.

3) х= +2πk, х= - + 2πk.

• х= π/4+πk, х=arctg5+πk.
• х= (-1) · π/6 + πn, х= 2πk.

1) 2со sx - = 0

2) sin2x =-

3) 2соs(x - ) = -1

4) tg²x - 6tgх+5=0

5) (2sinx – 1)( cosх-1)=0

2

4

Частные случаи

= -1, х= - k, k

= 1, х= k, k

= 0, х= k, k

= 0, х= k, k

= 1, х= k, k

= -1, х= k, k

х= k, k

х = k, k

х = - k, k

х= k, k

х = k, k

с х = - k, k

Тригонометрические неравенства

-1,arc+2πkarc+2πk, k

, х R

-1 arc+2πk arc+2πk, k

х R

-1,arc+2πk-аrc+2πk,k

, х R

-1,arc+2πkаrc+2πk,k

, х R

- k arctg, k

arctg k, k

arсctg , k

arctg, k