Презентация по математике "Решение треугольников"

Цель урока:

Повторение и систематизация знаний 

Закрепление навыков решения треугольников  с помощью формул

Формирование навыка выбора рационального способа решения задачи

Формирование умения работать самостоятельно, организовывать свое рабочее время, работать в группе

Воспитание у учащихся интереса к знаниям.

Треугольник является одной из основных геометрических фигур. Многие фигуры можно разбить на треугольники.

 Назовите их.

Определите вид треугольников ABC, MNB, ABК, BКС, MBО, NBО.

Тест на определение истинности (ложности) утверждения и правильности формулировок определений

В треугольнике против угла в 10° лежит большая сторона.

В равностороннем треугольнике внутренние углы равны между собой и каждый равен 60°.

Существует треугольник со сторонами: 2 см, 7 см, 3 см. 

Прямоугольный равнобедренный треугольник имеет равные катеты.

Если один из углов при основании равнобедренного треугольника равен 50°, то угол, лежащий против основания, равен 90°.

Геометрия. 9 класс Решение треугольников

Урок составила учитель математики ОСШГ№2

Власова Наталья Николаевна

Цель урока

• Повторение и систематизация знаний
• Закрепление навыков решения треугольников с помощью формул
• Формирование навыка выбора рационального способа решения задачи
• Формирование умения работать самостоятельно, организовывать свое

рабочее время, работать в группе

• Воспитание у учащихся интереса к знаниям

Треугольник и не только пройденного

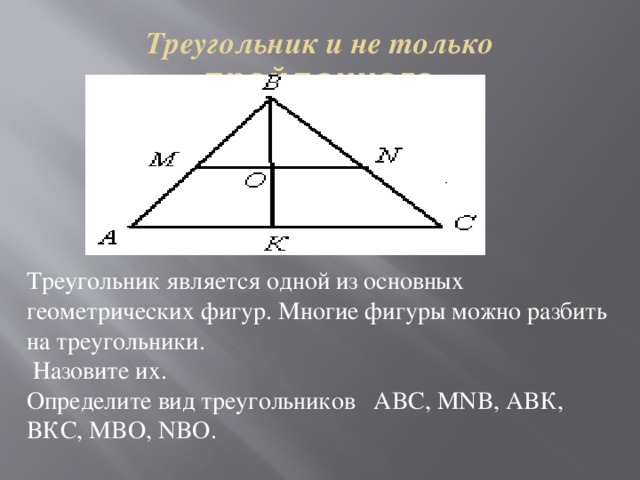
Треугольник является одной из основных геометрических фигур. Многие фигуры можно разбить на треугольники.

Назовите их.

Определите вид треугольников ABC, MNB, ABК, BКС, MBО, NBО.

Тест на определение истинности (ложности) утверждения и правильности формулировок определений

• В треугольнике против угла в 10° лежит большая сторона.
• В равностороннем треугольнике внутренние углы равны между собой и каждый равен 60°.
• Существует треугольник со сторонами: 2 см, 7 см, 3 см.
• Прямоугольный равнобедренный треугольник имеет равные катеты.
• Если один из углов при основании равнобедренного треугольника равен 50°, то угол, лежащий против основания, равен 90°.

• Если острый угол прямоугольного треугольника равен 60°, то прилежащий к нему катет равен половине гипотенузы.
• В равностороннем треугольнике все высоты равны.
• Сумма длин двух сторон любого треугольника меньше третьей стороны.
• Существует треугольник с двумя тупыми углами.
• В прямоугольном треугольнике сумма острых углов равна 90°.
• Если сумма двух углов меньше 90°, то треугольник тупоугольный.

Проверим ваши ответы

• В треугольнике против угла в 10° лежит большая сторона (Л)
• В равностороннем треугольнике внутренние углы равны между собой и каждый равен 60°(И)
• Существует треугольник со сторонами: 2 см, 7 см, 3 см (Л)
• Прямоугольный равнобедренный треугольник имеет равные катеты (И)
• Если один из углов при основании равнобедренного треугольника равен 50°, то угол, лежащий против основания, равен 90°(Л)

• Если острый угол прямоугольного треугольника равен 60°, то прилежащий к нему катет равен половине гипотенузы (И)
• В равностороннем треугольнике все высоты равны (И)
• Сумма длин двух сторон любого треугольника меньше третьей стороны (Л)
• Существует треугольник с двумя тупыми углами (Л)
• В прямоугольном треугольнике сумма острых углов равна 90°(И)
• Если сумма двух углов меньше 90°, то треугольник тупоугольный (И)

Диктант

• Один из углов прямоугольного треугольника равен 48°. Чему равен второй острый угол?
• В равнобедренном треугольнике одна сторона равна 70 см, другая 26 см. Чему равна длина основания?
• В треугольнике ABC ∠ В — наибольший. Какая из сторон треугольника наибольшая?
• Запишите теорему синусов.
• Запишите теорему косинусов.
• Какое отношение т еорема косинусов имеет к теореме Пифагора?

Проверим правильность выполнения диктанта

• Один из углов прямоугольного треугольника равен 48°. Второй острый угол равен 42 °.
• В равнобедренном треугольнике одна сторона равна 70 см, другая 26 см. Длина основания равна 26 см.
• В треугольнике ABC ∠ В — наибольший. Наибольшей является сторона АС.
• Теорема синусов:
• Теорема косинусов: а 2 = в 2 + с 2 – 2вс cos ∠ А .
• Теорему косинусов называют обобщенной теоремой Пифагора.

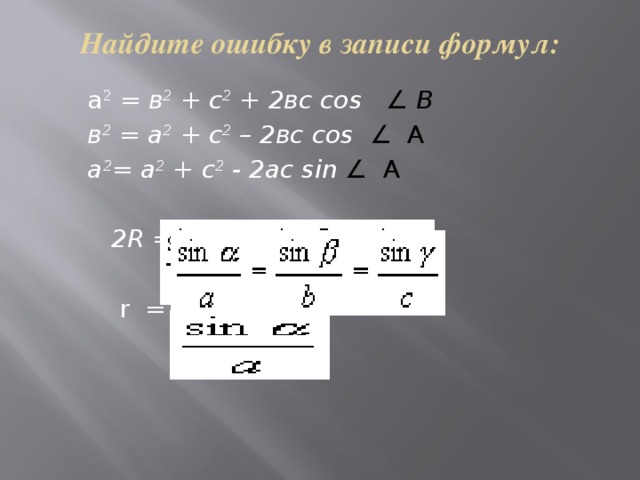
Найдите ошибку в записи формул:

а 2 = в 2 + с 2 + 2вc cos ∠ В

в 2 = а 2 + с 2 – 2вс cos ∠ A

а 2 = а 2 + с 2 - 2ас sin ∠ A

2R =

r =

Повторение материала

Немного теории

• Решением треугольника называется нахождение всех его шести элементов (т. е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
• При решении задач применяются теоремы синусов и косинусов, теорема о сумме углов треугольника и следствиия из теоремы синусов: в треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.

Задачи на решение треугольников

• решение треугольника по двум сторонам и углу между ними;
• решение треугольника по стороне и прилежащим к ней углам;
• решение треугольника по трем сторонам.

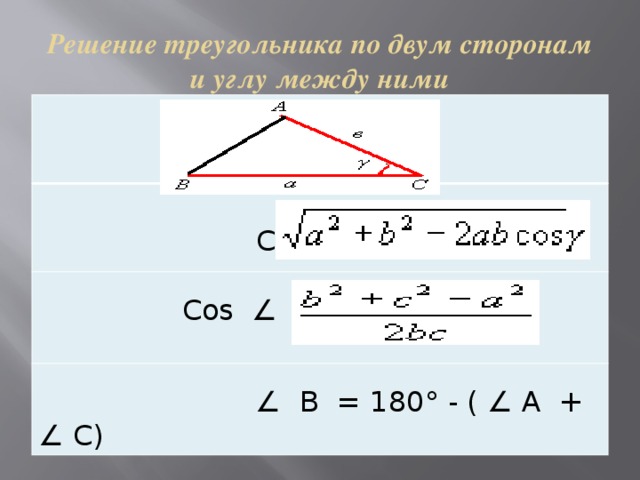
Решение треугольника по двум сторонам и углу между ними

С =

Cos ∠ A =

∠ В = 180° - ( ∠ А + ∠ С)

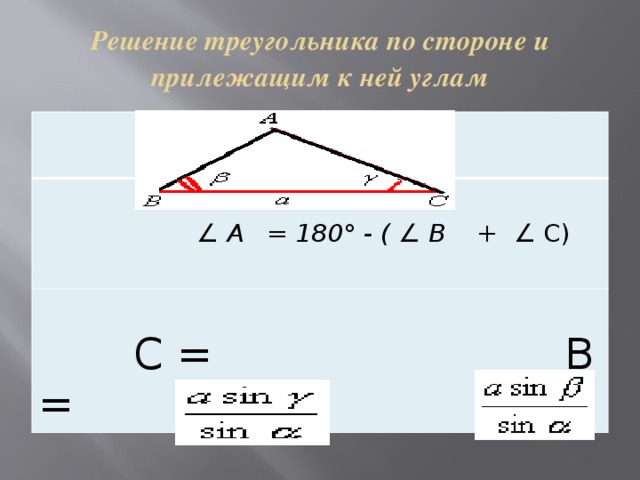
Решение треугольника по стороне и прилежащим к ней углам

∠ А = 180° - ( ∠ В + ∠ С)

С = В =

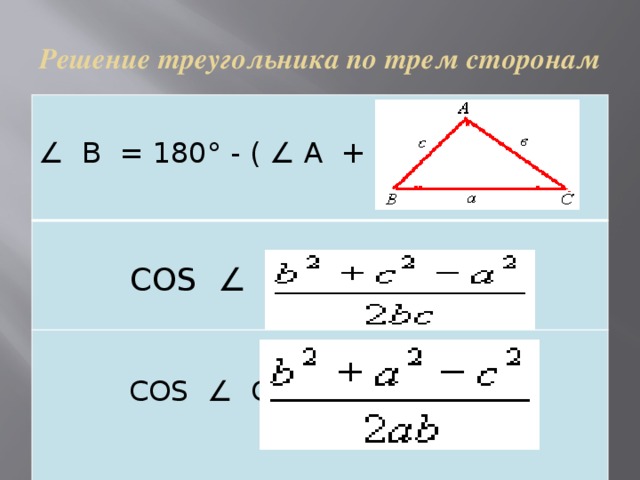
Решение треугольника по трем сторонам

∠ В = 180° - ( ∠ А + ∠ С)

COS ∠ A =

COS ∠ C =

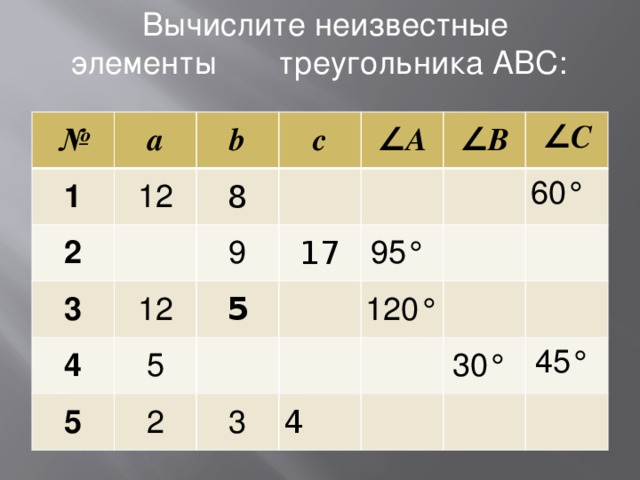
Вычислите неизвестные элементы треугольника АВС:

№

а

1

b

12

2

c

3

8

4

9

∠ A

12

17

∠ B

5

5

5

2

95°

∠ C

60°

3

120°

4

30°

45°

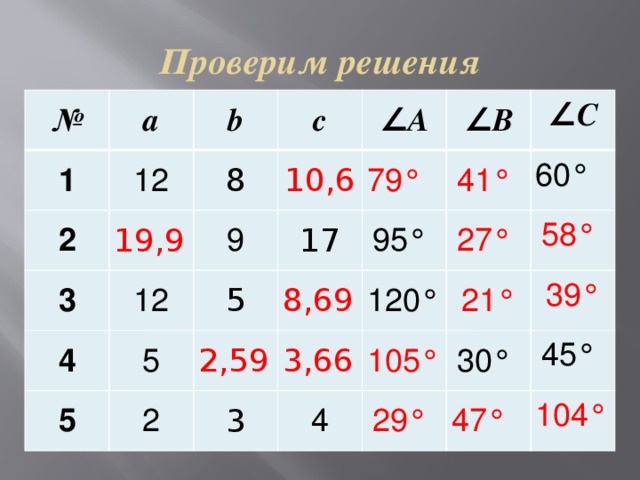
Проверим решения

№

а

1

2

b

12

8

19,9

c

3

∠ A

10,6

9

12

4

17

79°

∠ B

5

5

5

41°

∠ C

95°

2,59

2

8,69

27°

60°

120°

3,66

3

58°

21°

105°

4

39°

30°

29°

45°

47°

104°

Подведение итогов

• Что значит решить треугольник?
• Сколько существует типов задач на решение треугольников?
• Какие теоремы используются при решении треугольников?

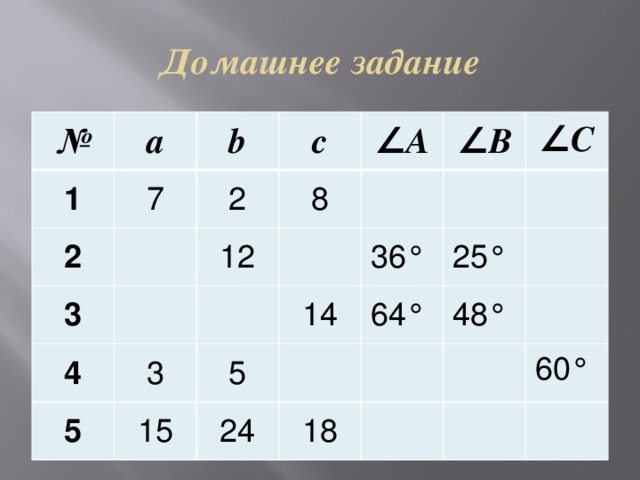
Домашнее задание

№

а

1

2

7

b

c

2

3

∠ A

4

8

12

∠ B

3

5

15

5

36°

14

∠ C

25°

64°

24

48°

18

60°