ПРОСТЫЕ ЧИСЛА
Учитель математики
МОУ Романовская СОШ
Корнева В.Н.
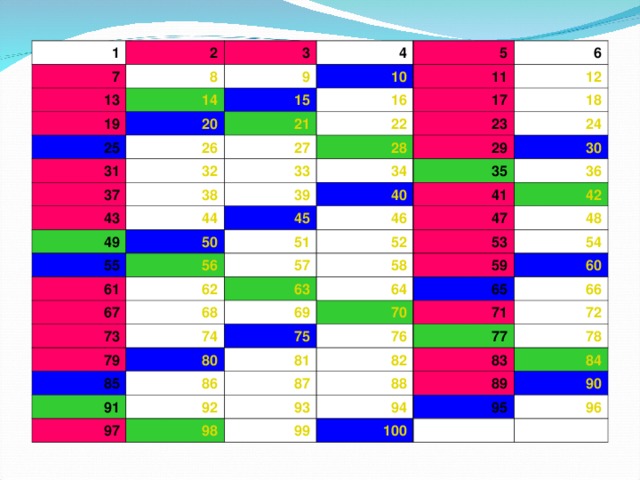
Решето Эратосфена
1
7
2
8
13
3
4
9
14
19
10
20
15
5
25
6
21
16
11
31
26
17
12
22
37
32
27
23
18
43
38
28
33
24
34
49
39
29
44
35
55
40
30
45
50
51
41
61
46
36
56
62
67
57
52
47
42
73
58
48
63
53
68
54
59
64
79
69
74
85
75
80
60
70
65
81
76
71
66
91
86
87
72
97
82
77
92
93
98
88
83
78
89
84
94
99
90
95
100
96
Решето Эратосфена
1
2
7
3
8
13
4
9
19
14
5
20
10
15
25
11
16
6
21
26
31
17
12
22
37
27
32
23
18
28
43
38
33
24
34
39
29
44
49
35
30
40
55
45
50
61
56
51
36
46
41
57
52
47
42
67
62
63
48
73
58
53
68
74
69
64
79
59
54
65
70
85
60
75
80
91
86
81
76
71
66
77
82
97
72
87
92
98
93
78
88
83
89
94
84
99
90
95
100
96
1
2
7
8
3
13
14
19
9
4
15
10
20
25
5
11
21
26
16
31
6
17
37
22
32
27
12
38
33
28
43
23
18
29
34
49
39
44
24
45
50
40
35
55
30
51
46
41
36
61
56
47
52
57
42
67
62
53
63
68
73
58
48
74
69
79
64
59
54
70
85
75
65
80
60
86
81
71
76
91
66
82
92
97
87
77
72
88
83
93
98
78
89
94
99
84
95
100
90
96
1
2
7
8
3
13
14
19
9
4
15
10
20
25
5
11
21
26
16
31
6
17
37
22
32
27
12
38
33
28
43
23
18
29
34
49
39
44
24
45
50
40
35
55
30
51
46
41
36
61
56
47
52
57
42
67
62
53
63
68
73
58
48
74
69
79
64
59
54
70
85
75
65
80
60
86
81
71
76
91
66
82
92
97
87
77
72
88
83
93
98
78
89
94
99
84
95
100
90
96
1
2
7
8
3
13
14
9
19
4
10
25
5
15
20
31
21
26
16
11
6
17
22
27
32
37
12
23
28
38
43
33
18
39
44
49
34
29
24
45
50
35
40
55
30
41
46
51
61
56
36
52
47
67
57
42
62
53
48
58
73
63
68
74
69
79
54
64
59
70
85
75
80
65
60
86
81
91
71
76
66
77
92
82
87
97
72
83
98
88
93
78
94
89
99
84
95
100
90
96
1
2
7
8
3
13
14
9
19
4
10
25
5
15
20
31
21
26
16
11
6
17
22
27
32
37
12
23
28
38
43
33
18
39
44
49
34
29
24
45
50
35
40
55
30
41
46
51
61
56
36
52
47
67
57
42
62
53
48
58
73
63
68
74
69
79
54
64
59
70
85
75
80
65
60
86
81
91
71
76
66
77
92
82
87
97
72
83
98
88
93
78
94
89
99
84
95
100
90
96
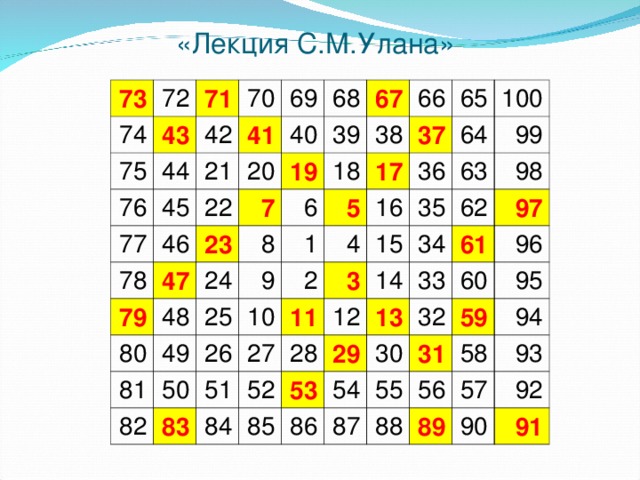
«Лекция С.М.Улана»
73
72
74
75
71
43
76
42
44
70
45
77
69
41
21
46
20
22
78
68
40
79
7
47
39
19
23
67
24
80
8
66
6
48
18
38
65
5
25
9
37
17
49
81
1
4
36
26
82
100
64
50
2
10
16
83
51
11
27
99
15
35
3
63
34
52
84
28
98
62
14
12
61
29
85
13
97
33
53
96
86
32
30
60
54
87
95
31
55
59
56
58
94
88
57
93
89
92
90
91
Есть ли самое большое простое число? Допустим, что существует последнее простое число. Обозначим его через N . Значит, по предположению, все числа, больше N , составные. Запишем произведение всех простых чисел от 2 до N : 2*3… N – и прибавим к произведению 1 . Тогда число К=2*3 *… N + 1 – целое и, по предположению, обязательно составное. Значит, К должно делиться хотя бы на одно простое число. Но при делении К на любое из простых чисел от 2 до N в остатке получится 1 . Следовательно, число К (поскольку оно составное) делится на простое число, которое больше N . Таким образом, предположение о том, что N наибольшее простое число, неверно.
Г.В.Дорофеев, Л.Г.Петерсон. 6 класс. (Часть 3). № 150.
Ошибка П.Ферма П.Ферма получил число 4 294 967 297 , которое не сумел разложить на множители, и думал, что оно тоже простое. Однако Эйлер (1707-1783) нашел, что это число делится на 641 . Таким образом, Эйлер показал, что Ферма ошибся.
Числа Мерсена Далее знакомимся с числами вида 2 p -1, где р - простое число. Они называются числами Мерсенна (1588-1648), который впервые заметил, что среди таких чисел много простых. В течение почти 200 лет математики подозревали, что число Мерсенна 2 67 -1простое. В 1903 г. Ф. Н. Коул показал, что число 2 67 -1 составное, так как оно равно произведению числа 193 707 721 на число 761 838 257 287 .
Победитель простых чисел
Первый и очень большой шаг в распределении простых чисел сделал великий русский ученый Пафнутий Львович Чебышев .
В 1850 г. Он доказал, что между любым натуральным числом, не равным 1 , и числом, в 2 раза большим его (т.е. между n и 2 n ), находится хотя бы одно простое число.
За эту теорему Чебышева назвали победителем простых чисел
Получите свидетельство
Вход
Презентация по математике "Простые числа" (1.01 MB)
0
935
45
Нравится
0
