Презентация по математике по теме "Призма"

Высота – это перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

Высота прямой призмы равна ее боковому ребру.

Прямая призма называется правильной, если ее основания правильные многоугольники.

Площадь полной поверхности призмы – сумма площадей всех ее граней. (S_полн )

Площадь боковой поверхности призмы сумма площадей ее боковых граней. (S_бок)

Объем призмы равен произведению площади основания на высоту. (V_пр)

Полную информацию смотрите в файле. 

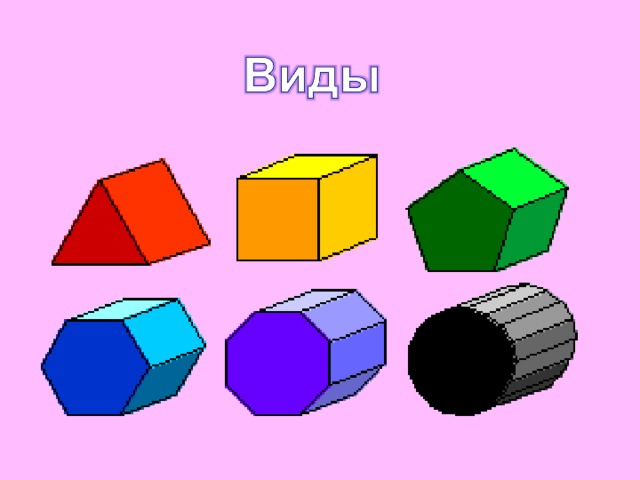
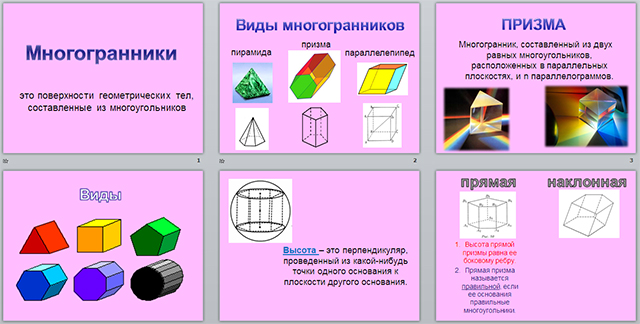
это поверхности геометрических тел, составленные из многоугольников

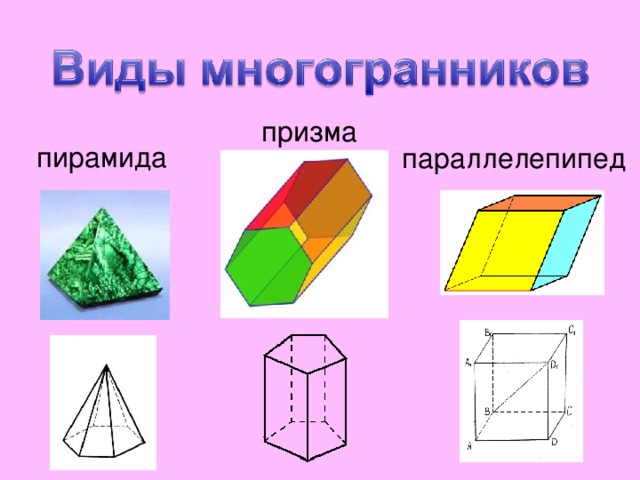
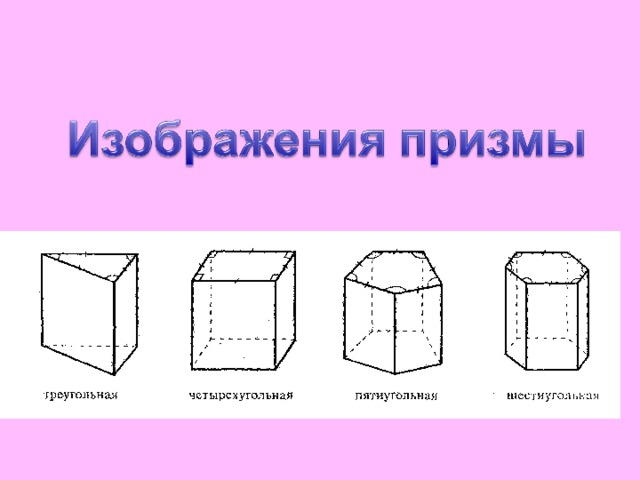
призма

пирамида

параллелепипед

Многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

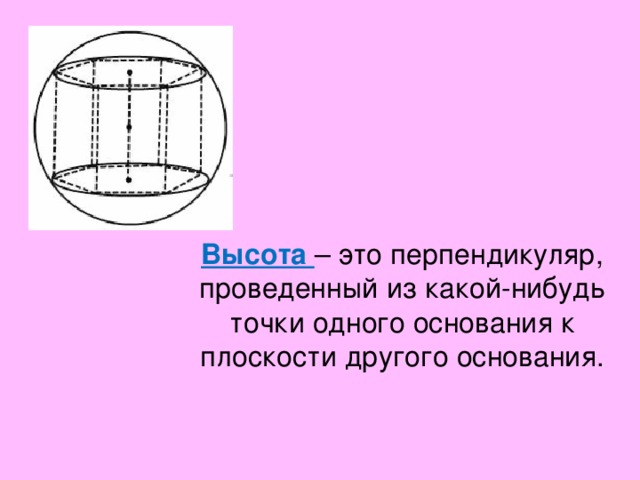
Высота – это перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

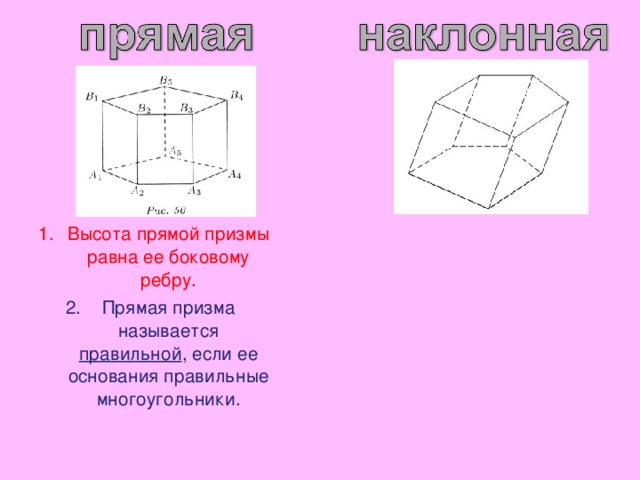
• Высота прямой призмы равна ее боковому ребру.

• Прямая призма называется правильной , если ее основания правильные многоугольники.

Площадь полной поверхности призмы – сумма площадей всех ее граней. ( S полн )

Площадь боковой поверхности призмы сумма площадей ее боковых граней. ( S бок )

S полн = S бок + 2 S осн

Объем призмы равен произведению площади основания на высоту. ( V пр )

V пр = S осн ▪ h

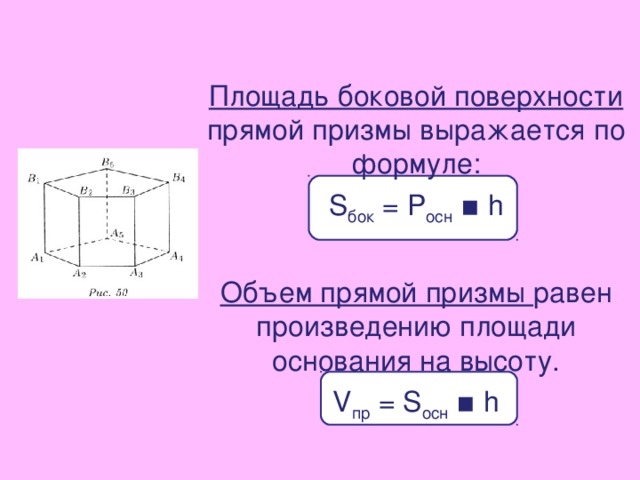
Площадь боковой поверхности прямой призмы выражается по формуле:

S бок = P осн ▪ h

Объем прямой призмы равен произведению площади основания на высоту.

V пр = S осн ▪ h

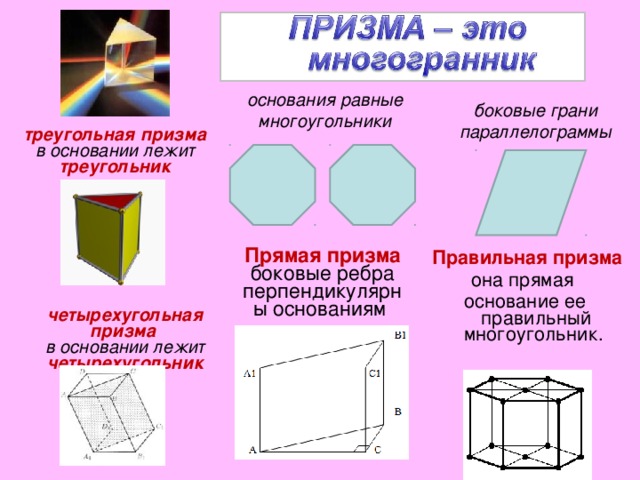
основания равные многоугольники

боковые грани параллелограммы

треугольная призма

в основании лежит треугольник

  Правильная призма

она прямая

основание ее правильный многоугольник. 

Прямая призма боковые ребра перпендикулярны основаниям

четырехугольная призма

в основании лежит четырехугольник

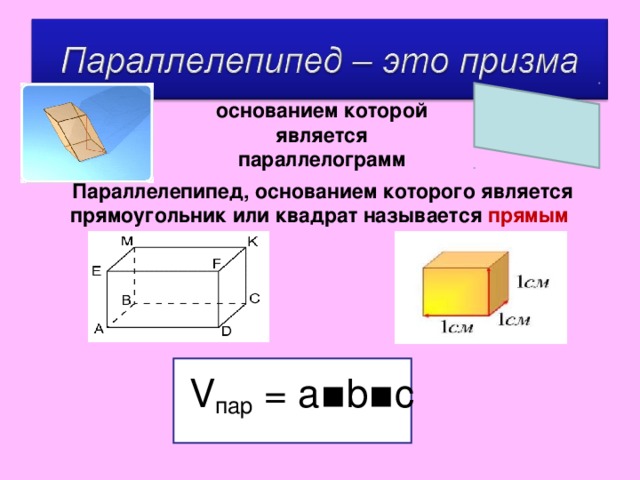
основанием которой является параллелограмм

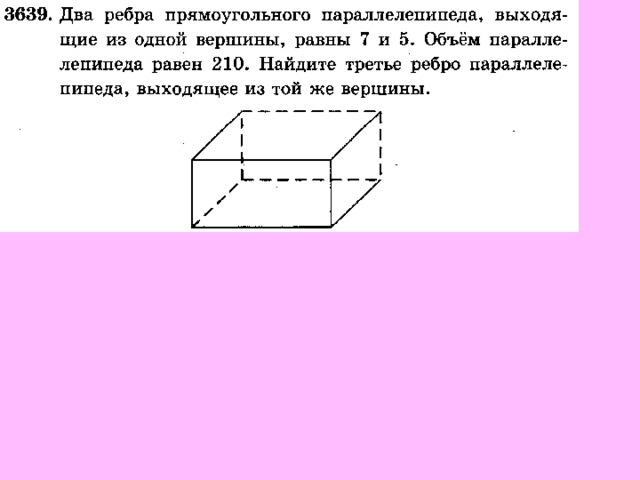
Параллелепипед, основанием которого является прямоугольник или квадрат называется прямым  

V пар = a▪b▪c

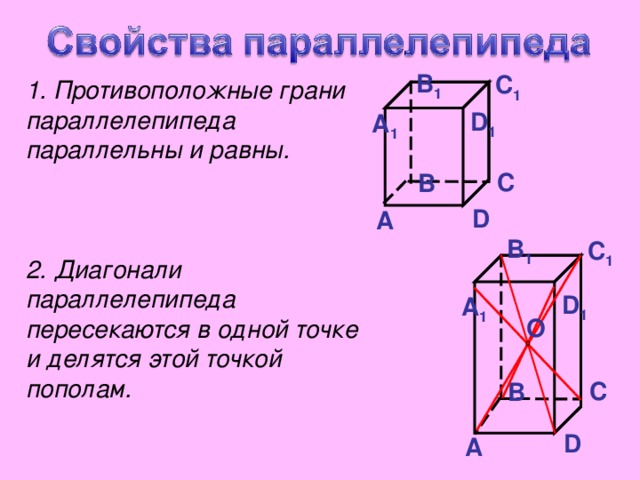
1. Противоположные грани параллелепипеда параллельны и равны.

2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

B 1

C 1

D 1

А 1

C

B

D

А

B 1

C 1

D 1

А 1

О

C

B

D

А