
Логарифмические уравнения
Кемерова Светлана Ильинична
Преподаватель математики
ГОУ СПО ТУ ЭТТ

Тема: логарифмические уравнения
- Опр. Логарифмическими уравнениями называются уравнения, в которых неизвестная находится под знаком логарифма или в основании логарифма.
- При решении логарифмических уравнений необходимо находить область допустимых значений переменной или выполнять проверку.

Методы решения
- 1. Использование определения
Логарифмом числа b по основанию a называется показатель степени, в которую необходимо возвести число a чтобы получить число b, где
Обозначается:
Т.е.

Методы решения
- 1. Использование определения
1. Решите уравнение:
Решение:
Используя определение логарифма, запишем:
Получим:
Найдем область допустимых значений переменной:
Так как х=21 принадлежит ОДЗ, то данный
корень является ответом уравнения.
Ответ: 12

Методы решения
- 2. Приведение к одному основанию с использованием основных свойств и формул

Методы решения
- 2. Приведение к одному основанию
1. Решите уравнение:
Решение:

- ОДЗ: Выражения, которые находятся под знаком логарифма, имеют ограничения:
ОДЗ:
Корни уравнения:
Принадлежат ОДЗ, значит являются решениями уравнения
Ответ: 1, 2

Методы решения
1. Решите уравнение:
Введем замену:
Получим:
Вернемся к замене:

- ОДЗ: Выражения, которые находятся под знаком логарифма, имеют ограничения:
Корни уравнения:
Принадлежат ОДЗ, значит являются решениями уравнения
Ответ:

Методы решения
Пример: loq4x = 1-х
Решение:
Построим в одной
сисиете координат
графики функций
и найдем их точку
пересечения
4.Графический:построение графиков функций в одной системе координат
Ответ: 1
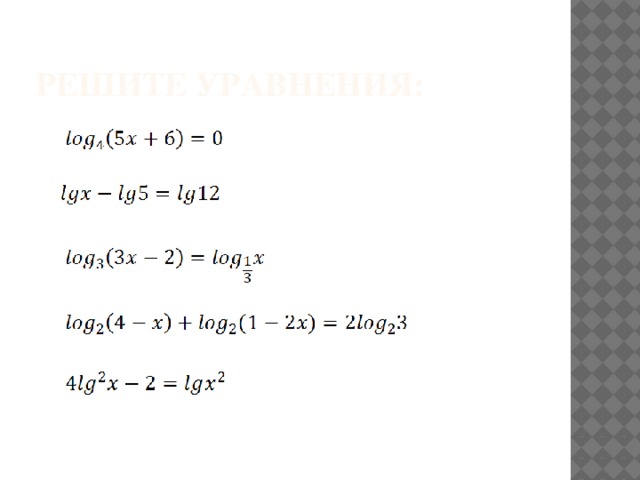
Решите уравнения:


 Получите свидетельство
Получите свидетельство Вход
Вход













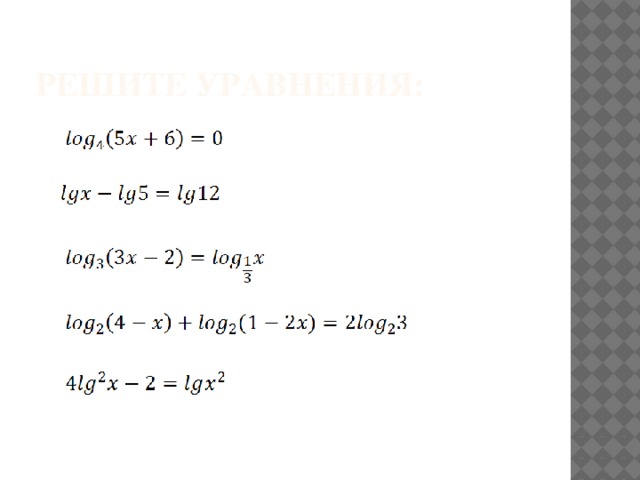









 Презентация по математике "Логарифмические уравнения" (0.17 MB)
Презентация по математике "Логарифмические уравнения" (0.17 MB)
 1
1 664
664 96
96 Нравится
0
Нравится
0


