Презентация "Наибольшее и наименьшее значения функции"

Презентация содержит 27 слайдов.

Теорема Вейерштрасса.

Непрерывная на отрезке [a;b] функция f принимает на этом отрезке наибольшее и наименьшее значения

Правило отыскания наибольшего и наименьшего  значений f.

1.  Найти f '(x);

2.  Найти точки, в которых  f '(x)=0 или f '(x) не существует и отобрать из них те, что лежат внутри отрезка [a;b] ;

3.  Вычислить значения функции y=f (x) на концах отрезка и в критических точках, принадлежащих данному отрезку.

4.Выбрать из них наибольшее и наименьшее, они будут соответственно  наибольшим и наименьшим, значением  функции  y = f (x)  на  отрезке [ a; b] , которые обозначаются так:

max f(x)               min f(x)
[a; b]                      [a;b]

Галерея «Известные ученые»

Галерея «Известные ученые»

Открытый урок по математике

Наибольшее и наименьшее значения функции.

«Много ли человеку земли надо….»

Математика и литература

Какой же четырёхугольник получился???

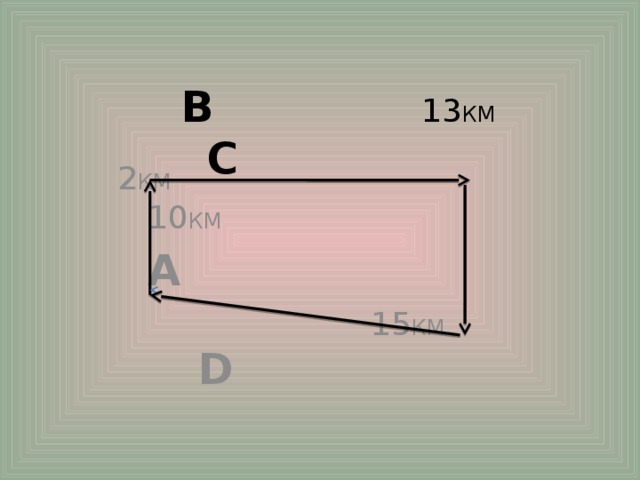
B 13 КМ C

2 КМ 10 КМ

A

15 КМ D

?

А что же такое Р ???

Р - ЭТО

Периметр

четырёх-

угольника…

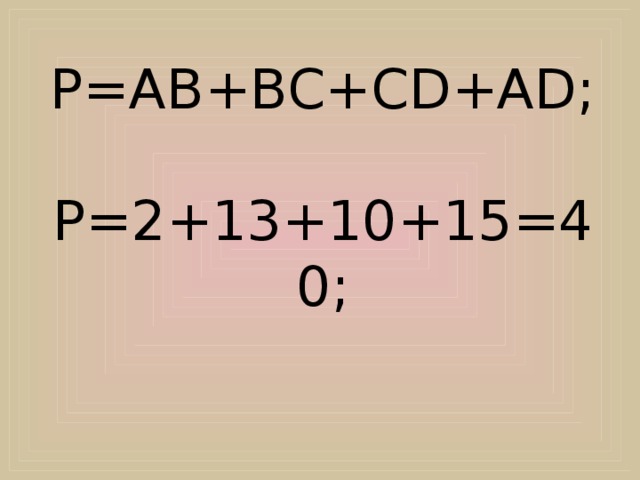
P=AB+BC+CD+AD; P=2+13+10+15=40;

Какую же площадь получил Пахом???

S=((AB+CD)/2)*BC;

S=((2+10 )/ 2)*13=78(Км 2 )

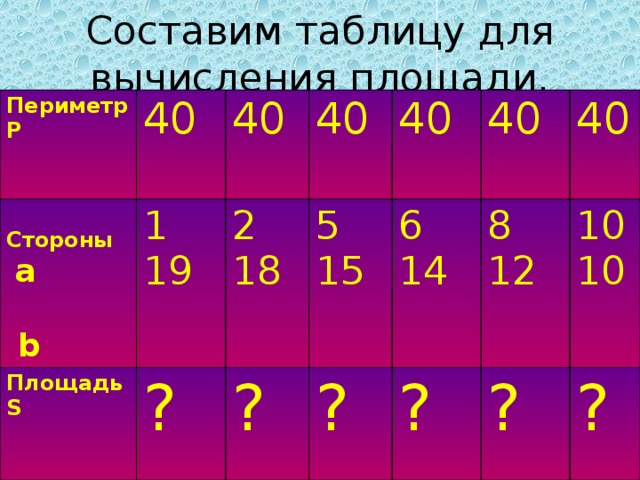
Составим таблицу для вычисления площади.

Периметр Р

40

40

Площадь S

Стороны а

1

40

?

b

19

2

?

5

40

18

15

6

?

40

14

8

?

40

?

10

12

10

?

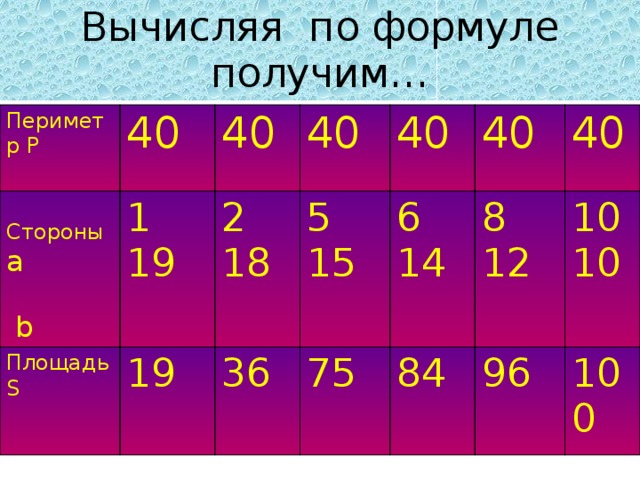
Вычисляя по формуле получим…

Периметр Р

40

1

Площадь S

Стороны a

40

40

19

19

b

2

36

40

18

5

75

15

40

6

8

14

40

84

12

96

10

10

100

Теорема Вейерштрасса.

Непрерывная на отрезке [a;b] функция f принимает на этом отрезке наибольшее и наименьшее значения

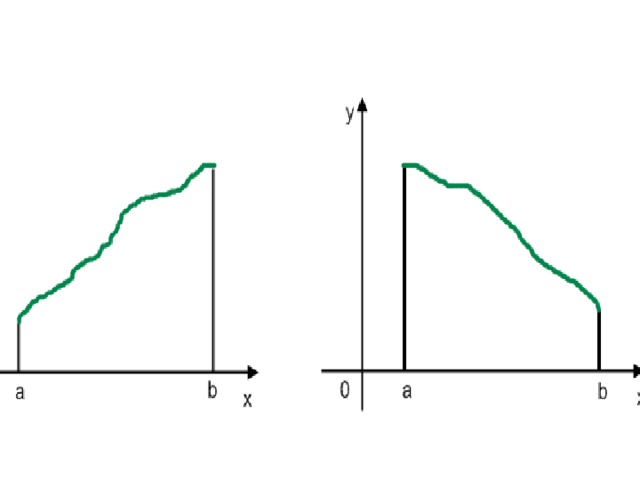
Правило отыскания наибольшего и наименьшего значений f.

1. Найти f (x) ;

2. Найти точки, в которых f (x)=0 или f (x) не существует и отобрать из них те, что лежат внутри отрезка [a;b] ;

3. Вычислить значения функции y=f (x) на концах отрезка и в критических точках, принадлежащих данному отрезку.

4. Выбрать из них наибольшее и наименьшее, они будут соответственно наибольшим и наименьшим, значением функции y = f (x) на отрезке [ a; b] , которые обозначаются так: max f(x) min f(x) [a; b] [a;b]

Наибольшее и наименьшее значения на отрезке

• Правило

• f ' (x)
• f ' (x)=0
• f ' не существует
• f(a); f(b); f(Х 1 ); f(Х 2 )

5.Выбрать наибольшее и наименьшее

Разберём пример 1 учебника

Найти наибольшее и наименьшее значение непрерывной функции

Y=x 3 -3x 2 -45x+225 на промежутке [0;6];

Y’= ;

Y’=0;

X 1 = ; X 2 = ;

Y’ существует при всех Х

Y(0)= ;

Y(5)= ;

Y(6)= ;

Вывод:

Порешаем???

Начнём!!!

Найти наибольшее и наименьшее значения функции на промежутке y=f (x)

Сравните наибольшее значение функции на промежутке P 1 и наименьшее её значение на промежутке P 2 :

F(x)= x 4 -2x 2 +4;

P 1 =[-1/2; 1/2], P 2 =[2;3];

БЛАГОДАРЮ ЗА ВНИМАНИЕ!!!