Росрыболовство
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Астраханский государственный технический университет»
Обособленное структурное подразделение «Волго-Каспийский морской рыбопромышленный колледж» федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Астраханский государственный технический университет»
Конкурс электронных презентаций
«Математика в экономике»
Автор:
преподаватель математики
ФГБОУ ВПО «АГТУ»
ОСП «ВКМРПК»
Земцов Д.В.
Астрахань, 2013
Цели мероприятия:
- формирование умений осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития;
- формирование информационной культуры, умения анализировать и оценивать информацию с использованием информационно-коммуникационных, в частности, мультимедийных технологий.
Материальное обеспечение:
Интерактивная доска, компьютер, проектор, зеркальная фотокамера.
Сценарий мероприятия
Вступительная речь преподавателя. Добрый день! Мы собрались здесь, чтобы провести конкурс компьютерных презентаций в программе Microsoft PowerPoint на тему «Математика в экономике». Конечно, математика интересна и полезна сама по себе для развития личности в целом и ее отдельных сторон, особенно, интеллекта, но не будем забывать, что она проникает во все области окружающей действительности, то есть математические законы – это универсальные законы материального мира. В частности, математика применяется в моделировании, прогнозировании экономических процессов.
Почему мы решили провести внеучебное мероприятие в такой форме, на стыке математики, экономики и информатики? Мы живем в информационном обществе. Сегодня одной из важнейших задач образования является формирование информационной компетентности, информационной культуры студентов. Что означает «информационная компетентность»? Согласно государственному стандарту образования для специальности 080114 Экономика и Бухгалтерский Учет (по отраслям) такой специалист должен уметь «осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач», «анализировать и оценивать информацию с использованием информационно-коммуникационных технологий».
Теперь представлю вам сегодняшних конкурсантов и членов жюри. Свои тематические презентации о применении математических методов в экономических науках подготовили студенты группы ЭБ-21: Ерасова Екатерина, Кардель Виктор, Красильникова Надежда, Кухарук Кристина, Новак Элина, Пахомова Валерия, Тагиева Ирада и Тамбаева Мадина.
Члены профессионального жюри: Чернявская Ольга Владимировна, преподаватель биологии и психологии общения, методист колледжа; Аникина Елена Юрьевна, преподаватель математики и информатики. Члены студенческого жюри: Гвоздикова Елизавета, Егиян Элина, Иралиева Роза, студенты группы ЭБ-3.
Презентации и выступления будут оцениваться по следующим критериям: 1) информативность презентации, 2) практическая направленность, 3) грамотность изложения, 4) качество оформления. Эти критерии предлагаю я. Есть ли у членов жюри другие предложения?
Итак, каждый член преподаватель-член жюри оценивает презентацию и выступление по этим позициям, а затем все баллы складываются и определяются победители. Объявляю начало конкурса!
Первый доклад «Решение экономических задач на оптимальный вариант с помощью производной» (Элина Новак).
Задачи на оптимальный вариант – это задачи экономического, технического, геометрического, естественнонаучного содержания, в которых требуется определить оптимальное (наибольшее или наименьшее) значение некоторой функциональной зависимости или условие, при котором значение достигается.
Производная функции - основное понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Она определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой в данной точке.
Приведем пример экономической задачи на оптимальный вариант, решаемой методом производной.
В кафе при цене 55 рублей за чашку кофе в среднем бывает 45 заказов в день. Если цену повысить до 60 рублей, то количество заказов снижается до 40 чашек кофе. Считая линейным соотношение между спросом и ценой, найти значение цены, при которой выручка достигает своего максимального значения. Каково максимальное значение выручки?
Задачи на оптимальный вариант удобно решать по следующему плану.
1) Выбрать оптимизируемую величину, обозначить ее через какую-нибудь букву в зависимости от содержания задачи, например, y.
2) Одну из неизвестных величин считать независимой переменной и обозначить, например, через x; установить реальные границы изменения x в соответствии с условиями задачи.
3) Исходя из условий задачи выразить y через x и неизвестные величины, то есть задать функцию y=f(x).
4) Для полученной функции y=f(x) найти наибольшее или наименьшее значение (в зависимости от требования задачи) по промежутку реального изменения x. Функцию исследовать с помощью производной.
5) Интерпретировать результат п. 4 для данной конкретной задачи.
Задача. Издержки производства некоторой продукции определяются функцией 15x²+240x, где x – число единиц произведенной за день продукции. Эта продукция продается по цене 840 рублей за изделие. Сколько изделий нужно произвести и продать, чтобы прибыль была максимальной?
Решение. Рассмотрим z(x) – функцию прибыли. Так как одна единица продукции продается за 840 рублей, а объем выпуска равен x изделий, то доход составит 840x. Прибыль равна разности дохода и издержек производства, поэтому
z(x)=840x-(15x²+240x)= -15x²+600x.
Исследуем составленную функцию на максимум с помощью производной.
1) Область определения функции
D(z)=(0; +∞),
так как цена – величина положительная.
2) Производная функции прибыли:
z`(x)= (-15x²+600x)`= -30x+600
3) Приравниваем производную к нулю и решаем полученное уравнение:
z`(x)=0
-30x+600=0
30x=600
x=20
x=20 – критическая точка.
4) Определяем знаки производной слева и справа от точки x=20:
z`(10)= -300+6000;
z`(30)= -900+600
Производная меняет знак с «плюса» на «минус», то есть x=20 – точка максимума. Так как функция прибыли непрерывна и имеет единственную точку экстремума (максимума), то в этой точке достигается наибольшее значение этой функции. Значит, максимальная прибыль достигается при объеме выпуска продукции, равном 20 изделий в день.
Второй доклад «Задача о непрерывном начислении процентов» (Ерасова Екатерина, Кардель Виктор).
Постановка этой задачи следующая. Первоначальный вклад в банк составил Q0 денежных единиц. Банк выплачивает ежегодно p% годовых. Необходимо найти размер вклада через Q1 лет.
При использовании простых процентов размер вклада ежегодно будет увеличиваться на одну и ту же величину 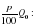
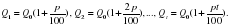
На практике значительно чаще применяются сложные проценты. В этом случае размер вклада ежегодно будет увеличиваться в одно и то же число (1+p/100) раз:
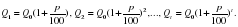
Если начислять проценты по вкладам не один раз в году, а n раз, то при том же ежегодном приросте p% процент начисления за 1/n-ю часть года составит p/n%, а размер вклада через t лет при nt начислениях составит
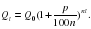

Будем полагать, что проценты по вкладу начисляются каждое полугодие (n=2), ежеквартально (n=4), ежемесячно (n=12), каждый день (n=365), каждый час (n=8760) и т.д., непрерывно (n→∞). Тогда размер вклада через t лет составит
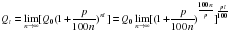
или с учетом замечательного предела при условии
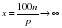
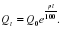
Последняя формула выражает показательный (экспоненциальный) закон роста (при p0) или убывания (при p
В качестве примера приведем в таблице размеры вкладов Qt, вычисленные при Q0=1 ден. ед., p=5%, t=20 лет.
|
| Формула простых процентов | Формула сложных процентов | Формула непрерывного начисления процентов |
|
n=1 |
n=2 |
n=4 |
n=12 |
n=365 |
|
| Размер вклада, ден. ед. |
2,000 |
2,636 |
2,685 |
2,702 |
2,713 |
2,718 |
2,718 |
Замечание. Хотя в практических финансово-кредитных операциях непрерывное начисление процентов применяется крайне редко, оно оказывается весьма эффективным при анализе сложных финансовых проблем, в частности при обосновании и выборе инвестиционных решений.
Третий доклад «Задачи линейного программирования» (Красильникова Надежда, Тамбаева Мадина).
Для того, чтобы понять что такое задачи линейного программирования, начнем с примера производной задачи.
Предприятие производит 2 вида продукции: П1 и П2 и использует для этого 4 вида сырья: С1, С2, С3, С4. Запасы сырья, число единиц сырья, затрачиваемого на изготовление 1 ед. продукции, и прибыль, получаемая от реализации 1 ед. продукции, - приведены в таблице:
| Вид сырья | Запас сырья | Количество ед. сырья, затрачиваемого на изготовление 1 ед. продукции |
| П1 | П2 |
| С1 | 18 | 1 | 3 |
| С2 | 16 | 2 | 1 |
| С3 | 5 | 0 | 1 |
| С4 | 21 | 3 | 0 |
| Прибыль от реализации 1 ед. продукции | 2 | 3 |
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.
Проанализировав условие задачи, составим ее математическую модель. Для этого обозначим x и y – количество единиц продукции 1-го и 2-го вида соответственно, которое необходимо произвести исходя из ограничения сырья и задачи максимизации прибыли. Имеем задачу с двумя неизвестными. Ее математическая модель состоит из двух частей: системы неравенств, выражающих сырьевые ограничения и функции прибыли, которую следует исследовать на максимум.
Далее такая система решается описанным ниже методом линейного программирования.
Задачи линейного программирования (далее - ЗЛП) – это задачи на оптимальное планирование хозяйственной деятельности (промышленной или сельскохозяйственной).
С точки зрения линейной алгебры, ЗЛП состоят в отыскании оптимального значения некоторой линейной функции нескольких переменных при выполнении системы условий, каждое из которых выражается линейным неравенством с теми же переменными . Целевая функция обычно представляет собой функцию прибыли (в этом случае она исследуется на максимум) или функцию затрат (в этом случае – на минимум).
Математическая модель ЗЛП состоит из:
1. Целевой функции–линейной функции двух переменных x, y;
2. Системы ограничений–системы неравенств с переменными x, y:
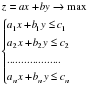
Алгоритм решения задач линейного программирования.
1) Проанализировав условие задачи, составить ее математическую модель.
2) Решить систему ограничений графическим методом, то есть в координатной плоскости.
3) Построить в той же координатной плоскости график целевой функции z = ax+by (например, при z=0) и обозначить вектор ее роста n=(a;b).
4) Параллельным переносом надвигая прямую целевой функции на область ограничений в направлении вектора n (при исследовании на максимум) или в противоположном направлении (при исследовании на минимум), зафиксировать точку выхода прямой из области; эта точка и выражает оптимальный план задачи.
5) Найти оптимальное значение целевой функции zmax или zmin, если в задаче это требуется.
Далее, ориентируясь на предложенный алгоритм, докладчики с помощью слайдов презентации объясняют решение приведенной задачи, получают следующий результат: оптимальный объем выпуска продукции составляет 6 единиц продукции первого вида и 4 единицы – второго вида; при этом максимальная прибыль составляет 24 денежной единицы.
Четвертый доклад «Применение матриц в экономике» (Кухарук Кристина).
Понятие матрицы часто используется в практической деятельности. Например, данные о выпуске продукции нескольких видов в каждом квартале года или нормы затрат нескольких видов ресурсов на производство продукции нескольких типов и т.д. удобно записывать в виде матриц. Далее докладчик приводит примеры применения алгебры матриц в экономике.
Пятый доклад «Сравнительный анализ конкурентного и монопольного рынков с помощью дифференциального исчисления» (Пахомова Валерия, Тагиева Ирада).
Применение дифференциального исчисления, то есть теории производных функций, к исследованию экономических объектов и процессов на основе анализа предельных величин получило название предельного анализа. Преимущество предельных величин в том, что они характеризуют не состояние, а процесс изменения, динамику развития экономического объекта. Таким образом, производная в экономике выступает как скорость изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора. Следует учесть, однако, что экономика не всегда позволяет использовать предельные величины в силу дискретности (прерывности) экономических показателей во времени (например, начисление процентов по вкладу один или несколько раз в год, а не непрерывно). Вместе с тем в ряде случаев можно пренебречь дискретностью показателей и эффективно использовать предельные величины.
В качестве примера рассмотрим соотношения между средним и предельным доходом в условиях монопольного и конкурентного рынков.
Суммарный доход (выручку) от реализации продукции z можно определить как произведение цены продукции y на количество продукции x, то есть z=yx.
В условиях монополии одна или несколько фирм полностью контролируют предложение определенной продукции, а следовательно, цены на них. При этом, как правило, с увеличением цены спрос на продукцию падает. Будем полагать, что это происходит по линейному закону, то есть функция y(x)=kx+b – линейная, убывающая (kb0). Тогда суммарный доход от реализованной продукции составит
z(x)=yx=x(kx+b)=kx²+bx
В этом случае средний доход на единицу продукции составит
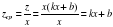
Предельный доход, то есть дополнительный доход от реализации единицы дополнительной продукции составит
z`(x)=(kx²+bx)=2kx+b.
Видим, что обе функции дохода – убывающие. Следовательно, в условиях монопольного рынка с ростом количества реализованной продукции предельный доход снижается, что приводит к уменьшению и среднего дохода.
В условиях совершенной конкуренции, когда число участников рынка велико, и каждая фирма не способна контролировать уровень цен, устойчивая продажа товаров возможна по преобладающей рыночной цене y=const. При этом суммарный доход составит
z=yx
В этом случае средний доход составит
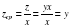
Предельный доход составит
z`(x)=(yx)`=y
Вывод: в условиях свободного конкурентного рынка средний и предельный доходы совпадают, причем, в отличие от монопольного рынка, с ростом реализованной продукции доход не снижается.

Заключение. Жюри подводит итоги, выставляя баллы по 5-балльной шкале по критериям (см. приложение):
1) информативность презентации;
2) практическая направленность;
3) грамотность изложения;
4) качество оформления.
Победителем признается презентация студентов Пахомовой Валерии и Тагиевой Ирады на тему «Сравнительный анализ конкурентного и монопольного рынков с помощью дифференциального исчисления».
Также отмечаются работы, занявшие второе и третье место. Ведущий отмечает достоинства каждой презентации, поощряет каждого выступающего, подводит итог о достигнутых целях мероприятия.
Приложение: критерии оценки электронной презентации.
|
| Информативность презентации | Практическая направленность | Грамотность изложения | Качество оформления | Сумма |
| Красильникова Н.В., Тамбаева М.А. «Задачи линейного программирования» |
|
|
|
|
|
| Кухарук К.Н. «Матрицы в экономике» |
|
|
|
|
|
| Ерасова Е.А., Кардель В.Н. «Задача о непрерывном начислении процентов» |
|
|
|
|
|
| Пахомова В.А., Тагиева И.Т. «Сравнительный анализ конкурентного и монопольного рынков» |
|
|
|
|
|
| Новак Э.Ф. «Задачи на оптимальный вариант экономической направленности» |
|
|
|
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход





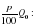
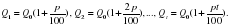
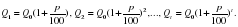
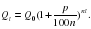

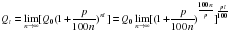
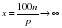
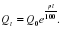

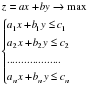

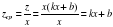
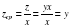










 Внеклассное мероприятие по математике "Математика в экономике" (0.47 MB)
Внеклассное мероприятие по математике "Математика в экономике" (0.47 MB)
 0
0 533
533 32
32 Нравится
0
Нравится
0


