Конспект урока по алгебре и началу анализа
для средних общеобразовательных учреждений
Выполнила студентка группы МДМ-210 Киреева Оля
Тема урока: «Применение производной для отыскания наибольших и наименьших значений величин»
Цели урока:
Образовательная: сформировать представление об алгоритме отыскания наименьшего и наибольшего значений; формировать навыки отыскания наибольших и наименьших значений непрерывной функции на промежутке.
Развивающая: формировать умения анализировать, сопоставлять данные, выводить логические следствия из данных предпосылок, умение делать выводы, оценивать влияние условий на результат; развивать логическое мышление учащихся.
Воспитательная: формировать умение концентрировать внимание, сосредотачиваться.
Методы обучения: дедуктивно-репродуктивный
Тип урока: урок изучения нового материала
Требования к ЗУН:
учащиеся должны знать:
- алгоритм отыскания наибольшего и наименьшего значения непрерывной функции на промежутке;
учащиеся должны уметь:
- находить наибольшее и наименьшее значение непрерывной функции на промежутке по алгоритму, изученному на уроке;
- применять алгоритм для нахождения наибольшего и наименьшего значения непрерывной функции на промежутке для решения задач.
Оборудование: компьютер, экран, проектор, мультимедиа презентация.
Литература:
Мордкович, А.Г. и др. «Алгебра и начала анализа. Задачник для 10-11 класса» / А.Г. Мордкович и др. - М.: Мнемозина, 2001.
Мордкович, А.Г. «Алгебра и начала анализа. 10-11 класс. Учебник» / А.Г. Мордкович. - М.: Мнемозина, 2001. - 335с.
Стефанова, Н.Л. «Методика и технология обучения математике. Курс лекций». / Н.Л. Стефанова, Н.С. Подходова. - М.: Дрофа, 2005. – 416 с.
План урока:
Организационный момент (2 минуты)
Актуализация знаний (6 минут)
Изучение нового материала (20 минут)
Закрепление изученного материала (11 минут)
Подведение итогов (4 минуты)
Домашнее задание (2 минута)
ХОД УРОКА
1. Организационный момент.
Включает в себя приветствие учителем класса, проверку готовности кабинета к проведению урока, проверку отсутствующих.
2. Актуализация знаний.
Учитель: Прежде чем приступить к изучению нового материала, прошу вас обратить внимание на доску: на слайде изображены графики одной и той же функции
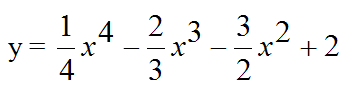
на разных отрезках ее области определения (слайд 2).
Рассмотрим отдельно каждый чертеж:
а) по чертежу определить, в каких точках функция принимает наименьшее и наибольшее значение (слайд 2):
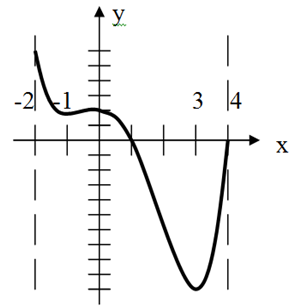
Учащиеся по очереди выходят к доске и записывают ответ.
Ученик: минимальное значение функции на данном отрезке равно -10:
| Запись на доске и в тетрадях:
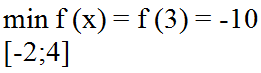
|
Ученик: максимальное значение функции на данном отрезке равно 6:
| Запись на доске и в тетрадях:
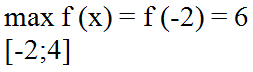 |
Учитель: проверим ответы.
На слайде появляются ответы (слайд 2).
Учитель: б) по чертежу определить, в каких точках функция принимает наименьшее и наибольшее значение (слайд 3):
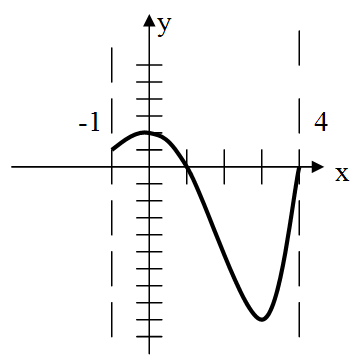
Учащиеся по очереди выходят к доске и записывают ответ.
Ученик: минимальное значение функции на данном отрезке равно -9:
| Запись на доске и в тетрадях:
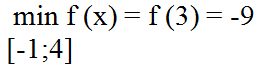 |
Ученик: максимальное значение функции на данном отрезке равно 2:
| Запись на доске и в тетрадях:
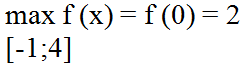 |
Учитель: проверим ответы.
На слайде появляются ответы (слайд 3).
Учитель: в) по чертежу определить, в каких точках функция принимает наименьшее и наибольшее значение (слайд 4):
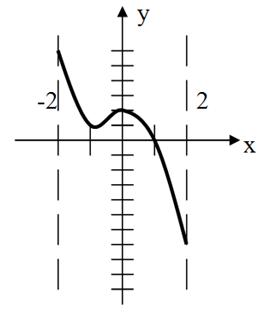
Учащиеся по очереди выходят к доске и записывают ответ.
Ученик: минимальное значение функции на данном отрезке равно -7:
| Запись на доске и в тетрадях:
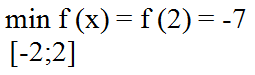 |
Ученик: максимальное значение функции на данном отрезке равно 6:
| Запись на доске и в тетрадях:
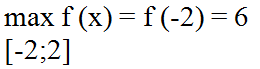 |
Учитель: проверим ответы.
На слайде появляются ответы (слайд 4).
Учитель: Из курса 7-го класса вы умеете строить графики функций и находить по ним минимальные и максимальные значения. Однако, построение графика данной функции заняло бы очень много времени. Сегодня на уроке мы рассмотрим способ нахождения минимальных и максимальных значений без построения графика. Минимальные и максимальные значения одним словом называют экстремальными, или экстремумами.
3. Изучение нового материала.
Учитель: Откройте свои тетради и запишите сегодняшнее число и тему урока «Применение производной для отыскания наибольших и наименьших значений величин».
Запись на доске (слайд 5) и в тетрадях:
Дата «…»
Тема: «Применение производной для отыскания наибольших и наименьших значений величин»
Учитель: Большая группа задач в технике, в естествознание, в экономике, в повседневной деятельности людей связана с необходимостью определения условий, при которых некоторая величина принимает наибольшее или наименьшее значения.
Например:
1) Где нужно расположить мост через реку, чтобы путь из А в В, находящихся на разных берегах, был наименьшим?
2) Требуется огородить участок с заданным периметром, чтобы площадь его была наибольшей (если перевести эту задачу на язык математики: какой из всех прямоугольников заданного периметра имеет наибольшую площадь?)
Такие задачи объединяют также одним названием – задачи «Дидоны».
Они названы так по имени легендарной основательницы города Карфаген и её первой жрицы. Согласно легенде, вынужденная бежать из своего родного города, Дидона вместе со своими спутниками прибыла на северный берег Африки и хотела приобрести у местных жителей землю для нового поселения. Ей согласились уступить участок земли, однако не больше, чем объемлет воловья шкура. Хитроумная Дидона разрезала воловью шкуру на узкие ремешки и, разложив их, сумела ограничить гораздо большую площадь по сравнению с той, которую можно было покрыть одной воловьей шкурой.
Как видите, решение задач на нахождение наиболее выгодных условий занимали умы людей с древних времен. Но только с появлением дифференциального исчисления был найден метод, позволяющий решать эти задачи по единой схеме, которую мы с вами сегодня изучим.
Учитель: Для того, чтобы найти наибольшее и наименьшее значения функции
y=f (x) на отрезке [a; b] нужно:
Найти область определения функции и определить, принадлежит ли заданный отрезок области определения.
Найти производную заданной функции f`(x).
Найти стационарные точки: f`(x) = 0;
Выяснить, какие из стационарных точек принадлежат данному отрезку [a; b].
Найти значения функции в тех стационарных точках, которые входят в отрезок, а также f (a) и f (b).
Выбрать из полученных значений функции наибольшее и наименьшее:
max f (x) = min f (x) =
[a; b] [a; b]
Учитель: Это алгоритм нахождения наибольшего и наименьшего значений функции
y=f (x) на отрезке [a; b]. Запишите его себе в тетрадь.
Учащиеся записывают с доски алгоритм в тетрадь (слайды 6,7,8)
| Запись в тетрадях:
Алгоритм нахождения наибольшего и наименьшего значений функции
y=f (x) на отрезке [a; b]: для того, чтобы найти наибольшее и наименьшее значения функции
y=f (x) на отрезке [a; b] нужно: 1. Найти область определения функции и определить, принадлежит ли заданный отрезок области определения. 2. Найти производную заданной функции f`(x). 3. Найти стационарные точки: f`(x) = 0; 4. Выяснить, какие из стационарных точек принадлежат данному отрезку [a; b]. 5. Найти значения функции в тех стационарных точках, которые входят в отрезок, а также f (a) и f (b). 6. Выбрать из полученных значений функции наибольшее и наименьшее: max f (x) = min f (x) = [a; b] [a; b] |
Учитель: А теперь рассмотрим пример применения данного алгоритма: найдем наибольшее и наименьшее значения функции f (x) = 2x3-9x2 на [1;4].
Учащиеся вместе с учителем у доски разбирают пример применения алгоритма, отвечают на наводящие вопросы и делают записи в тетради
Учитель: Что нужно сделать в первую очередь?
Ученик: Нужно найти область определения и определить, принадлежит ли данный отрезок этой области определения, функция определена на R, следовательно, отрезок принадлежит области определения.
Учитель: Следовательно, отрезок будет принадлежать области определения.
Ученик: Затем нужно найти производную функции f `(x) = 6x2-18х = 6x(x-3).
Учитель: Теперь найдите стационарные точки.
Ученик: Стационарные точки: f `(x) = 0; х = 0 или х = 3.
Учитель: Принадлежат ли они заданному отрезку?
Ученик: 0 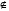 [1;4], 3
[1;4], 3 [1;4].
[1;4].
Учитель: Найдите значение функции в стационарных точках и на концах отрезка.
Ученик: f (3) = 54-81 = -27; f (1) = 2-9 = -7; f (4) = 128-144 = -16.
Учитель: Каковы экстремумы функции?
Ученик: max f (x) = f (1) = -7; min f (x) = f (3) = -27;
[1;4] [1;4]
| Запись на доске и в тетрадях:
Найти наибольшее и наименьшее значения функции f (x) = 2x3-9x2 на отрезке [1;4].
1) функция определена и дифференцируема на R;
2) f `(x) = 6x2-18х = 6x(x-3);
3) стационарные точки: f `(x) = 0; х = 0 или х = 3;
4) 0 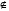 [1;4], [1;4], 3 [1;4]. [1;4].
5) f (3) = 54-81 = -27; f (1) = 2-9 = -7; f (4) = 128-144 = -16.
6) max f (x) = f (1) = -7; min f (x) = f (3) = -27; [1;4] [1;4] |
Учитель: А теперь обратите внимание на доску и проверьте, верно ли вы записали пример.
На слайде появляется решение, с которым учащиеся сверяют свои записи (слайд 9)

4. Закрепление изученного материала.
Учитель: Перейдем к решению задач. Первый номер 939 (а).
Учащиеся выходят по очереди к доске, решают примеры, комментируют решение, остальные – решают на месте, делая записи в тетради.
Ученик: найдите экстремумы функции у=12х2 на промежутке [-1;2].
Учитель: Найдем область определения функции.
Ученик: Функция определена на R, значит указанный промежуток принадлежит области определения.
Учитель: Какие действия делаем далее?
Ученик: Найдем производную функции у`=24х, стационарная точка х=0.
Учитель: Принадлежит ли точка заданному отрезку?
Ученик: 0 [-1;2]; найдем значение функции в стационарной точке и на концах отрезка у(0)=0, у(-1)=12, у(2)=48. Следовательно,
[-1;2]; найдем значение функции в стационарной точке и на концах отрезка у(0)=0, у(-1)=12, у(2)=48. Следовательно, 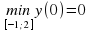 ;
; 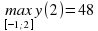 .
.
Запись на доске и в тетрадях:
Найти: экстремумы у=12х2 на [-1;2].
Решение:
у=12х2 определена на R; у`=24х;
у`=0 при х=0; 0 [-1;2];
[-1;2];
у(0)=0, у(-1)=12, у(2)=48;
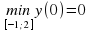 ;
; 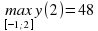 .
.
Учитель: Следующий номер 938 (а)
Учащиеся выходят по очереди к доске, решают примеры, комментируют решение, остальные – решают на месте, делая записи в тетради.
Ученик: Найдите экстремумы функции у=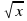 на промежутке [0;9].
на промежутке [0;9].
Учитель: Найдем область определения функции.
Ученик: Функция определена на (0;+∞), значит указанный промежуток принадлежит области определения.
Учитель: Какие действия делаем далее?
Ученик: Найдем производную функции у`=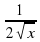 , у`≠0 при любых х.
, у`≠0 при любых х.
Учитель: Принадлежит ли точка заданному отрезку?
Ученик: Найдем значение функции на концах отрезка у(0)=0, у(9)=3.
Следовательно, 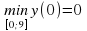 ;
; 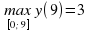 .
.
Запись на доске и в тетрадях:
Найти: экстремумы у=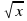 на [0;9].
на [0;9].
Решение:
у=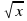 определена на (0;+∞); у`=
определена на (0;+∞); у`=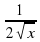 ;
;
у`≠0 при любых х; у(0)=0, у(9)=3,
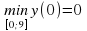 ;
; 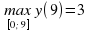 .
.
Учитель: Следующий номер 936 (а).
Учащиеся выходят по очереди к доске, решают примеры, комментируют решение, остальные – решают на месте, делая записи в тетради.
Ученик: Найдите экстремумы функции у=3х2-18х+504 на промежутке[0;3].
Учитель: Найдем область определения функции.
Ученик: Функция определена на R, значит указанный промежуток принадлежит области определения.
Учитель: Какие действия делаем далее?
Ученик: Найдем производную функции у`=6x-18, стационарная точка х=3.
Учитель: Принадлежит ли точка заданному отрезку?
Ученик: 3 [0;3]; найдем значение функции в стационарной точке и на концах отрезка у(3) = 477, у(0) = 504. Следовательно, ; .
[0;3]; найдем значение функции в стационарной точке и на концах отрезка у(3) = 477, у(0) = 504. Следовательно, ; .
Запись на доске и в тетрадях:
Найти: экстремумы у=3х2-18х+504 на [0;3].
Решение:
у=3х2-18х+504 определена на R; у`=6x-18;
у`=0 при х=3; у(3)=477, у(0)=504,
; .
5. Подведение итогов.
Учитель: Сегодня на уроке вы в целом хорошо поработали; те учащиеся, которые работали у доски, получают соответствующие отметки. Давайте повторим, как одним словом называют минимум и максимум функции?
Учащиеся по очереди отвечают на поставленные учителем вопросы.
Ученик: Минимум и максимум функции называют экстремумами.
Учитель: Какой алгоритм мы с вами сегодня изучили?
Ученик: Алгоритм нахождения наибольшего и наименьшего значений функции y=f (x) на отрезке [a; b].
Учитель: Назовите действия, входящие в алгоритм.
Ученик:
Найти область определения функции и определить, принадлежит ли заданный отрезок области определения.
Найти производную заданной функции f`(x).
Найти стационарные точки: f`(x) = 0;
Выяснить, какие из стационарных точек принадлежат данному отрезку [a; b].
Найти значения функции в тех стационарных точках, которые входят в отрезок, а также f(a) и f(b).
Выбрать из полученных значений функции наибольшее и наименьшее
…
6. Домашнее задание.
Учитель: Запишите домашнее задание, номера показаны на слайде (слайд 10):
| Запись в дневниках:
№№ 936, 958, 939 |

 Получите свидетельство
Получите свидетельство Вход
Вход






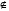 [1;4], 3
[1;4], 3 [1;4].
[1;4].
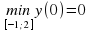 ;
; 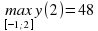 .
.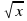 на промежутке [0;9].
на промежутке [0;9]. 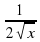 , у`≠0 при любых х.
, у`≠0 при любых х.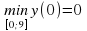 ;
; 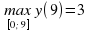 .
.








 Конспект урока по алгебре и началу анализа "Применение производной для отыскания наибольших и наименьших значений величин" (0.22 MB)
Конспект урока по алгебре и началу анализа "Применение производной для отыскания наибольших и наименьших значений величин" (0.22 MB)
 0
0 2048
2048 275
275 Нравится
0
Нравится
0




