
Логарифмы
и их свойства
Презентацию подготовила:
преподаватель математики Кравченко С. В.
Ставропольский край
г. Нефтекумск
ГБОУ СПО «НРПК»

Цель урока:
- Ввести понятие логарифма.
- Научиться находить значение логарифма.
- Вывести простейшие свойства логарифмов.
- Развивать умения самостоятельного подхода к решению задач.
- Содействовать вычислительной культуре студентов.
- Способствовать овладению студентов навыками математического моделирования.

Организационный момент
«Математика приводит в порядок неупорядоченное, выкорчевывает глупости, фильтрует грязное, дает явность стилю». Ж.А. Фабр
Последуем совету ученого: будем на уроке активны, внимательны, будем «поглощать» знания с большими желаниями, ведь скоро нам понадобятся для успешной сдачи экзамена.
Перед нами стоит задача: научиться находить логарифмы, при работе с логарифмами уметь применять их свойства.
Сегодняшний урок пройдёт в форме соревнования.
В первенстве победителем становится учащийся, набравший наибольшее количество карточек.

1 . Устный счёт
Представьте в виде степени с основанием 2 число:
а) 8; б) ; в) ; г) ; д)4;
Представьте в виде степени с основанием 10 число:
а)0,1; б) ; в)10; г) 0,1*1000;

Решите уравнение: а) =0,1 ; в) = б) = ; г) Вычислите: а) ; в) б) ; г)

Изобретение логарифмов
Изобретение логарифмов в начале XVII в. тесно связано с развитием в XVI в. производства и торговли, астрономии и мореплавания, требовавших усовершенствования методов вычислительной математики.
Все чаще требовалось быстро производить громоздкие действия над многозначными числами, все точнее и точнее должны были быть результаты действий.
Вот тогда-то и нашла воплощение идея логарифмов, ценность которых состоит в сведении сложных действий III ступени (возведения в степень и извлечения корня) к более простым действиям II ступени (умножению и делению), а последних - к самым простым, к действиям I ступени (сложению и вычитанию).

Первые таблицы логарифмов составлены независимо друг от друга шотландским математиком Дж. Непером(1550 - 1617) и швейцарцем И. Бюрги (1552 - 1632). В таблицы Непера, изданные в книгах под названиями "Описание удивительной таблицы логарифмов" (1614 г.) и "Устройство удивительной таблицы логарифмов" (1619 г.), вошли значения логарифмов синусов, косинусов и тангенсов для углов от 0 до 90 с шагом в 1 минуту. Бюрги подготовил свои таблицы логарифмов чисел, по-видимому, к 1610 г., но вышли в свет они в 1620 г., уже после издания таблиц Непера, и поэтому остались незамеченными.
Логарифмы необычайно быстро вошли в практику. Изобретатели логарифмов не ограничились разработкой новой теории. Было создано практическое средство - таблицы логарифмов, - резко повысившее производительность труда вычислителей.

Логарифмическая спираль в природе
Раковина наутилуса
Расположение семян
на подсолнечнике
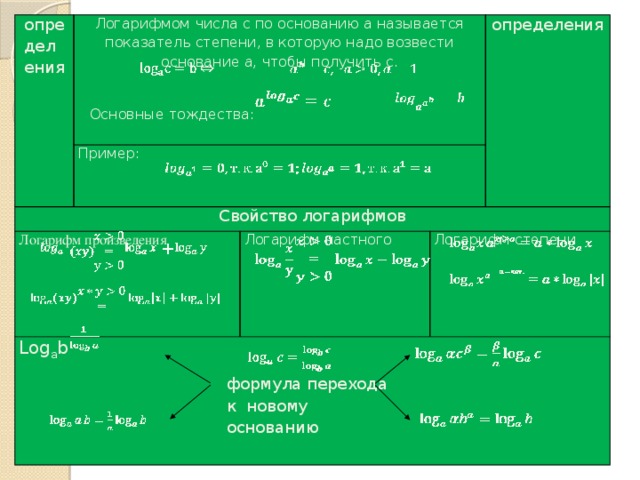
определения
Логарифмом числа с по основанию а называется показатель степени, в которую надо возвести основание а, чтобы получить с.
Пример:
Свойство логарифмов
Логарифм произведения
Log a b
Основные тождества:
определения
Логарифм частного
Логарифм степени
+
формула перехода к новому основанию

Игра
«Перестрелка»
Командам показывается слайд . Учитель. Поднимите руку те, кто хотя бы раз играл в «Морской бой»? Ну тогда вы легко справитесь со следующем заданием. На слайде вы видите таблицу. Учитель называет по горизонтали число, а по вертикали букву (например,2А). Тот студент, который первый даст правильный ответ получает – сигнальную карточку и продолжает игру (вычислить устно) . ( Учитель по ключу следит за правильностью ответов и подает сигнал продолжения игры).
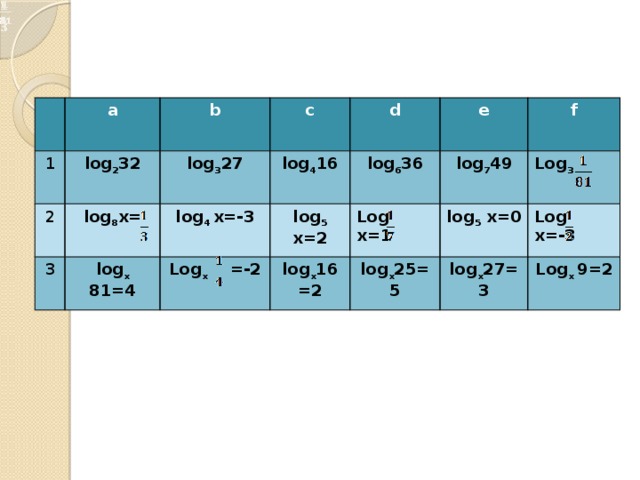
1
a
log 2 32
b
2
log 8 x=
log 3 27
c
3
log 4 16
log 4 x=-3
d
log x 81=4
log 5 x=2
log 6 36
e
Log x =-2
Log x=1
f
log 7 49
log x 16=2
log 5 x=0
Log 3
log x 25=5
Log x=-3
log x 27=3
Log x 9=2

.
Закрепление
;
1.Вычислите:
1)
2)10 /g0,3
ответ: 1) 2; 2)0, 3
2. Имеет ли смысл выражение Log₃ (-5)? log₂0? Почему?
3.При каких x имеет смысл выражение:
1) lg 2) Ig x²;
4.Запишите данное равенство с помощью логарифма:
1)2³=8; 2)

5.Верно ли равенство lg x²=2lg x?
6.Вычислить: а) б)log₄ log₂ log₃ ⁸¹;
7.Прологарифмировать равенство x= ?
При каких a и b это возможно?
8.Представить число 2 в виде логарифма некоторого числа с основанием 3, число -9 в виде логарифма с основанием 10; число 1 в виде логарифма числа с основанием 2.
9.Вычислить: 1)
2)
10.Определить знак выражения:
1)
2)

Практическая работа
1 вариант 2 вариант
1.При каких х имеет смысл выражение: 1) 1)
2. Запишите данное равенство с помощью логарифма:
1) 1)
3.Вычислите:
1) 1)
2) 2)
4.Определите знак выражения :
1) 1)

Практическая работа (проверка)
1 вариант 2 вариант 1. При каких х имеет смысл выражения: 1) 1) Ответ: при т. к. Ответ: при т.к. 2.Запишите данное равенство с помощью логарифма: 1) 1) 2) 2) 3. Вычислите: 1) 1)
2) 2)
4.Определите знак выражения:
т.к т.к
Ответ(+) Ответ(+)

Итог урока
- Какую тему урока мы сегодня рассмотрели ?
- Какая учебная задача была поставлена на уроке ?
- Справились ли вы с УЗ?
- Дайте определение логарифма ?
- С какими свойствами логарифмов вы познакомились? Перечислите их.
- Поставьте себе оценку. Для этого найдите свой балл (т.е. среднее арифметическое).

Интернет ресурсы
- http://prezentacii.com/matematike/6736-logarifmy.html
- http://club-edu.tambov.ru/vjpusk/vjp141/rabot/10/new_page_3.htm

 Получите свидетельство
Получите свидетельство Вход
Вход




























 Логарифмы и их свойства (0.67 MB)
Логарифмы и их свойства (0.67 MB)
 0
0 666
666 29
29 Нравится
0
Нравится
0


