Презентация к уроку геометрии "Теорема Пифагора"

Презентация  предназначена  для  урока  изучения  и  закрепления  нового  материала по  теме  "теорема  Пифагора".

Презентация  выполнена  в  соответствии  с  требованиями  ФГОС  второго  поколения. 

Она содержит  постановку  проблемы,  разминку,  доказательство  теоремы,  задачи  на  первичное  закрепление,  а  также  дополнительный  материал  в  виде  старинных  задач.

Историческая  справка

Существует замечательное соотношение между гипотенузой и катетами прямоугольного треугольника, справедливость которого была доказана древнегреческим философом и математиком Пифагором ( VI в. до н. э.).

Но изучение вавилонских клинописных таблиц и древних китайских рукописей показало, что это утверждение было известно задолго до Пифагора.

Заслуга же Пифагора состояла в том, что он открыл доказательство этой теоремы.

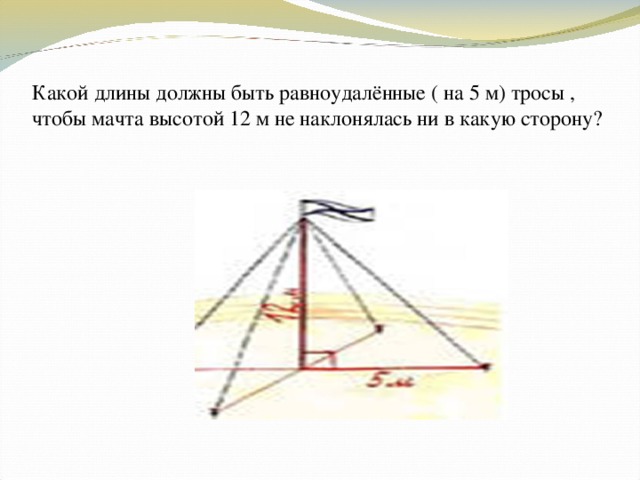
Какой длины должны быть равноудалённые ( на 5 м) тросы , чтобы мачта высотой 12 м не наклонялась ни в какую сторону?

• Познакомиться с теоремой Пифагора, запомнить ее.
• Научиться применять её при решении задач.

Историческая справка

Разминка

Формулировка теоремы Пифагора

Доказательство теоремы

Решение задач

Заключение

Историческая справка

• Существует замечательное соотношение между гипотенузой и катетами прямоугольного треугольника, справедливость которого была доказана древнегреческим философом и математиком Пифагором ( VI в. до н. э.).

• Но изучение вавилонских клинописных таблиц и древних китайских рукописей показало, что это утверждение было известно задолго до Пифагора.

• Заслуга же Пифагора состояла в том, что он открыл доказательство этой теоремы.

Пифагоровы штаны во все стороны равны

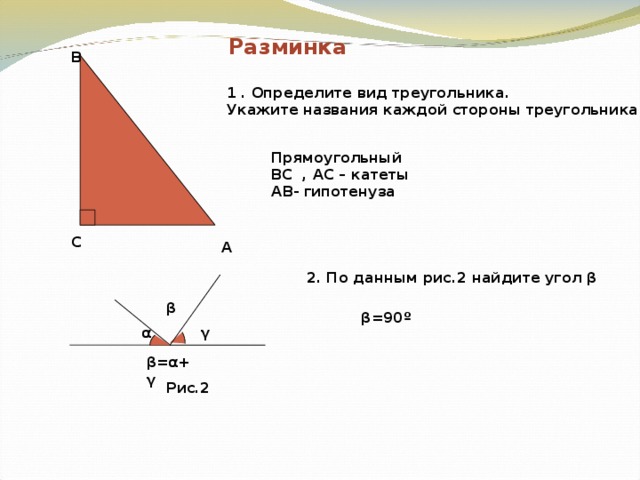
Разминка

B

1 . Определите вид треугольника.

Укажите названия каждой стороны треугольника

Прямоугольный

BC , AC – катеты

AB- гипотенуза

C

A

2. По данным рис.2 найдите угол β

β

β =90 º

γ

α

β = α + γ

Рис.2

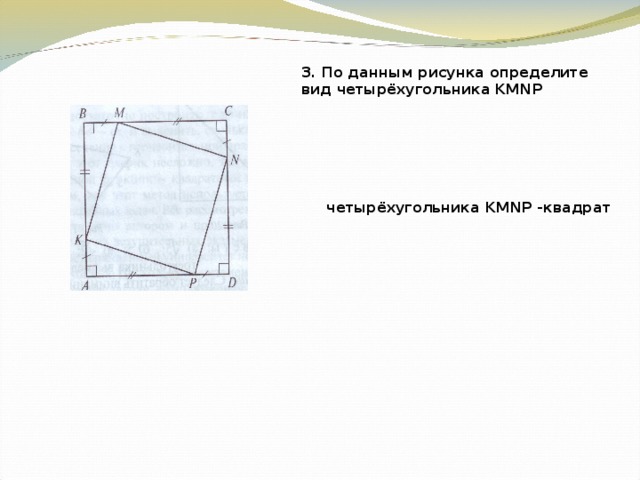
3. По данным рисунка определите вид четырёхугольника KMNP

четырёхугольника KMNP -квадрат

Формулировка теоремы

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

В

А

С

Доказательство теоремы

АВС,

Дано:

Доказать: с 2 = а 2 + в 2

Доказательство:

1. Достроим

АВС до квадрата СКРД со стороной ( а + в );

S СКРД = ( а + в) 2 = а 2 + 2ав + в 2

2.

МДВ ( по двум катетам )

ЕРМ =

ВСА =

АКЕ =

S ВСА = S АКЕ = S ЕРМ = S МДВ = ав /2

3 . ВАЕМ – квадрат, S ВАЕМ = c 2

4. S СКРД = S ВАЕМ + S ВСА + S АКЕ + S ЕРМ + S МДВ

5. ( а + в) 2 = с 2 + 4 * ав / 2

а 2 + 2ав + в 2 = с 2 + 2ав, откуда

с 2 = а 2 + в 2

Стихотворение ,которое помогает запомнить теорему Пифагора

АС 2 = 1 + 4 = 5, АС = √5 см Ответ : АС = √5 см. 2.Дан прямоугольный треугольник KMN . KN = 12c м, KM = 13см. Найти MN. Т. К. треугольник прямоугольный, то применим теорему Пифагора: с 2 = а 2 + в 2 КМ 2 = KN 2 + NM 2 = MN 2 =KM 2 – KN 2 = MN 2 = 169 -144 = 25, MN = 5 см Ответ : MN = 5 см. " width="640"

1. Вычислите сторону АС треугольника АВС

Т. К. треугольник прямоугольный, то применим теорему Пифагора: с 2 = а 2 + в 2

АС 2 = АВ 2 + ВС 2 = АС 2 = 1 + 4 = 5, АС = √5 см

Ответ : АС = √5 см.

2.Дан прямоугольный треугольник KMN .

KN = 12c м, KM = 13см. Найти MN.

Т. К. треугольник прямоугольный, то применим теорему Пифагора: с 2 = а 2 + в 2

КМ 2 = KN 2 + NM 2 = MN 2 =KM 2 – KN 2 = MN 2 = 169 -144 = 25, MN = 5 см

Ответ : MN = 5 см.

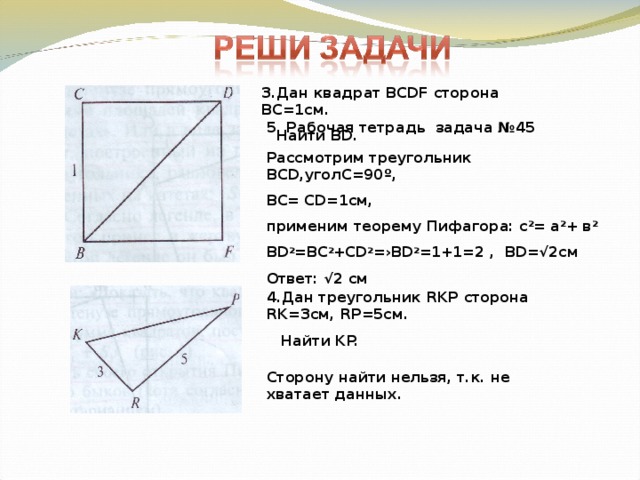
3.Дан квадрат ВС DF сторона ВС=1см.

Найти BD.

5. Рабочая тетрадь задача №45

Рассмотрим треугольник ВС D ,уголС=90 º ,

BC= CD=1c м,

применим теорему Пифагора: с 2 = а 2 + в 2

BD 2 =BC 2 +CD 2 =›BD 2 =1+1=2 , BD=√2c м

Ответ: √2 см

4.Дан треугольник RKP сторона RK = 3 см, RP=5c м.

Найти KP.

Сторону найти нельзя, т.к. не хватает данных.

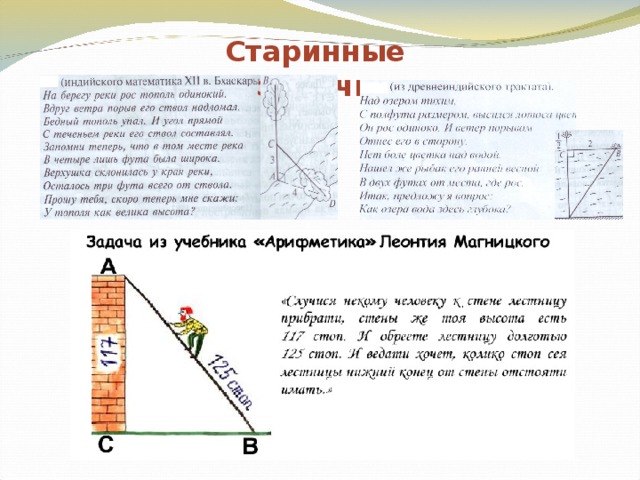
Старинные задачи

С какой теоремой мы сегодня познакомились?

Для каких треугольников она применима?

Сформулируйте теорему Пифагора.

Чему научились сегодня на уроке?