Презентация к уроку алгебры на тему «Тригонометрические функции»

Свойства функции у =cos x.

1) D (cos x) = R

2) - 1 <= cos x <= 1

3) cos (- x) = cos x

функция четная, график функции симметричен относительно оси ординат

4) cos (x + 360°) = cos x

T = 360° - наименьший положительный период

5) [ 0°; 360°]

функция возрастает от -1 до 1 при 180° < x < 360°

функция убывает от 1 до - 1 при 0° < x < 180°

6) cos x = 1, x = 0°, x = 360°; cos x = - 1, x = 180°  

Свойства функции у =sin x.

1) D (sin x) = R

2) - 1 <= sin x <= 1

3) sin (- x) = - sin x

функция нечетная, график функции симметричен относительно начала координат

4) sin (x + 360°) = sin x

T = 360° - наименьший положительный период

5) [ 0°; 360°]

функция возрастает от 0 до 1 при 0 < x < 90, 270 < x < 360

функция убывает от 1 до - 1 при 90 < x < 270

6) sin x = 1, x = 90°; sin x = - 1, x = 270°.

x

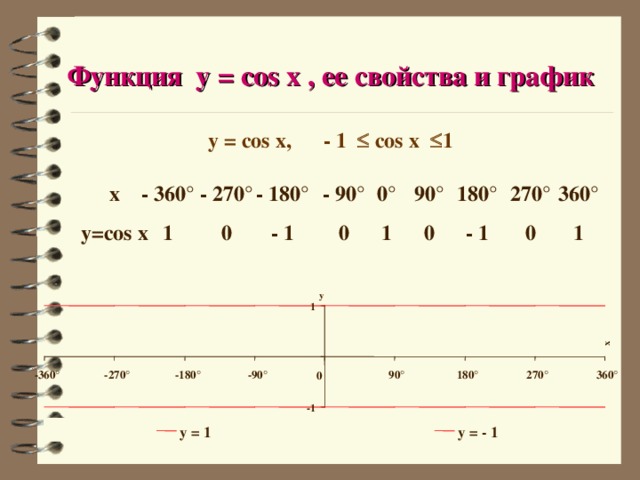
Функция y = cos x , ее свойства и график

y = cos x, - 1  cos x  1

360°

1

270°

0

180°

- 1

90°

0

0°

1

- 90°

0

- 180°

- 1

x

y=cos x

- 270°

0

- 360°

1

y

1

90°

180°

270°

360°

-360°

-180°

-270°

-90°

0

-1

y = 1

y = - 1

2

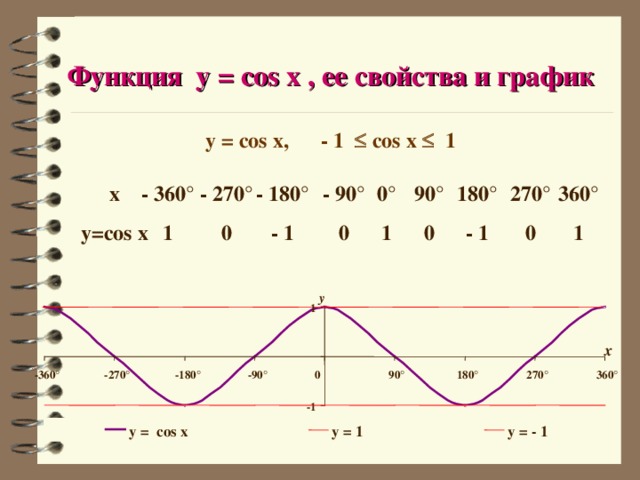
Функция y = cos x , ее свойства и график

y = cos x, - 1  cos x  1

- 90°

0

- 270°

0

x

y=cos x

360°

1

270°

0

180°

- 1

90°

0

0°

1

- 180°

- 1

- 360°

1

y

1

х

180°

-270°

360°

-360°

90°

270°

-180°

-90°

0

-1

y = 1

y = cos x

y = - 1

x

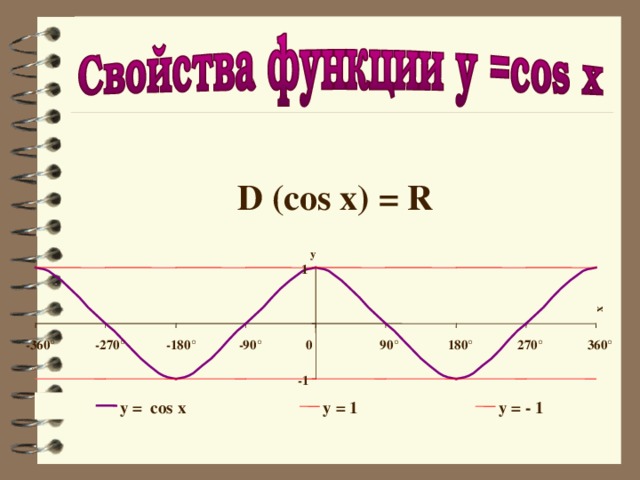
D (cos x) = R

y

1

270°

360°

90°

180°

0

-90°

-180°

-270°

-360°

-1

y = cos x

y = 1

y = - 1

x

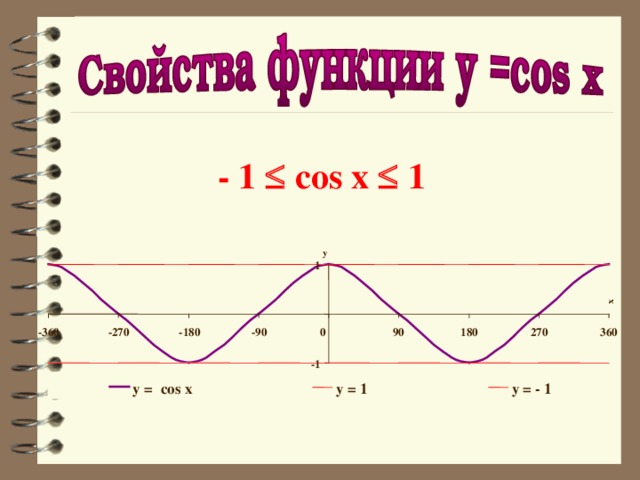
- 1  cos x  1

y

1

270

360

90

180

-360

0

-90

-180

-270

-1

y = cos x

y = 1

y = - 1

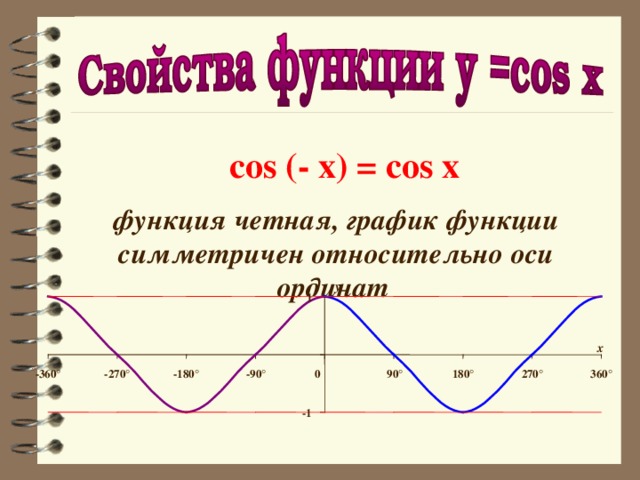
cos (- x) = cos x

функция четная, график функции симметричен относительно оси ординат

y

1

х

-360°

-180°

-90°

0

90°

180°

270°

360°

-270°

-1

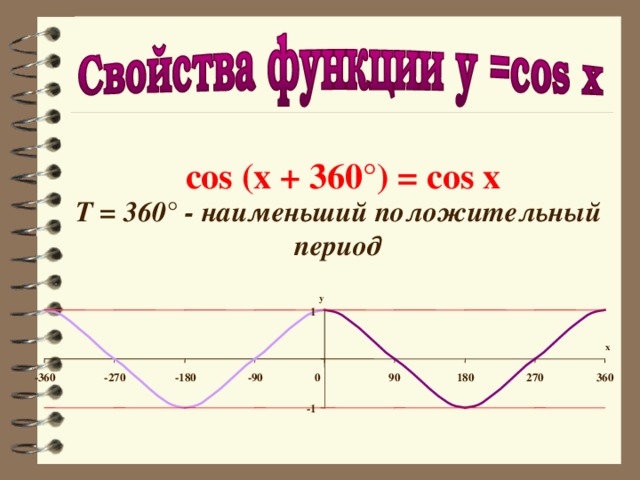
cos (x + 360°) = cos x

T = 360° - наименьший положительный период

y

1

x

-360

-180

-90

0

90

180

270

360

-270

-1

x

[ 0; 360°]

функция возрастает от -1 до 1 при 180°

функция убывает от 1 до - 1 при 0°

y

1

0

90

180

270

360

-1

x

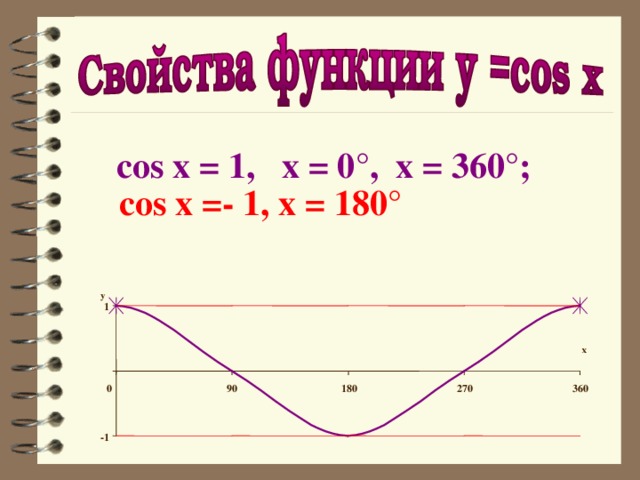
cos x = 1, x = 0°, x = 360°;

cos x =- 1, x = 180°

y

1

0

90

180

270

360

-1

x

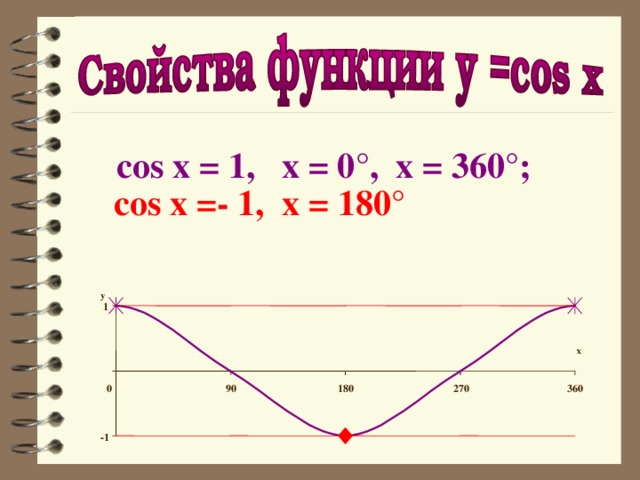
cos x = 1, x = 0°, x = 360°;

cos x =- 1, x = 180°

y

1

0

90

180

270

360

-1

1) D (cos x) = R

2) - 1  cos x  1

3) cos (- x) = cos x

функция четная, график функции симметричен

относительно оси ординат

4) cos (x + 360°) = cos x

T = 360° - наименьший положительный период

5) [ 0°; 360°]

функция возрастает от -1 до 1 при 180°

функция убывает от 1 до - 1 при 0°

6) cos x = 1, x = 0°, x = 360°; cos x = - 1, x = 180°

x

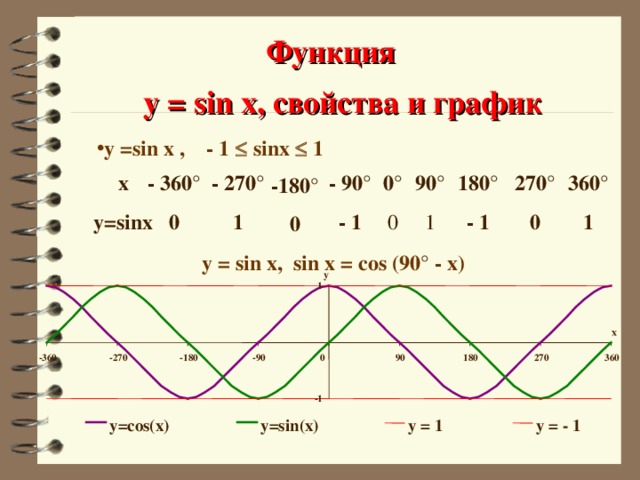
Функция

y = sin x, свойства и график

• y =sin x , - 1  sinx  1

-180°

0

360°

1

90°

1

180°

- 1

270°

0

0°

0

- 90°

- 1

- 270°

1

- 360°

0

x

y=sinx

y = sin x, sin x = cos (90 ° - x)

y

1

360

90

270

180

0

-90

-180

-270

-360

-1

y=cos(x)

y=sin(x)

y = 1

y = - 1

1) D (sin x) = R

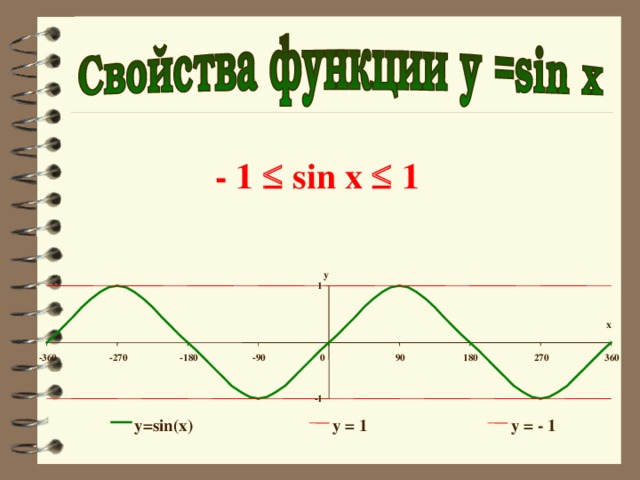
- 1  sin x  1

y

1

x

270

360

90

180

0

-90

-180

-270

-360

-1

y=sin(x)

y = 1

y = - 1

x

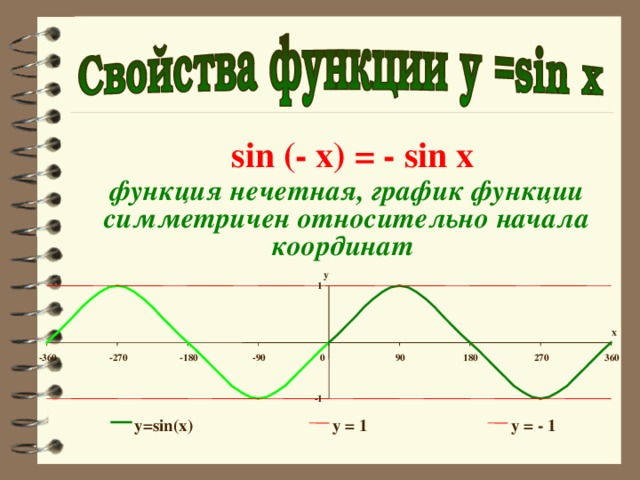
sin (- x) = - sin x

функция нечетная, график функции симметричен относительно начала координат

y

1

270

360

90

180

0

-90

-180

-270

-360

-1

y=sin(x)

y = 1

y = - 1

x

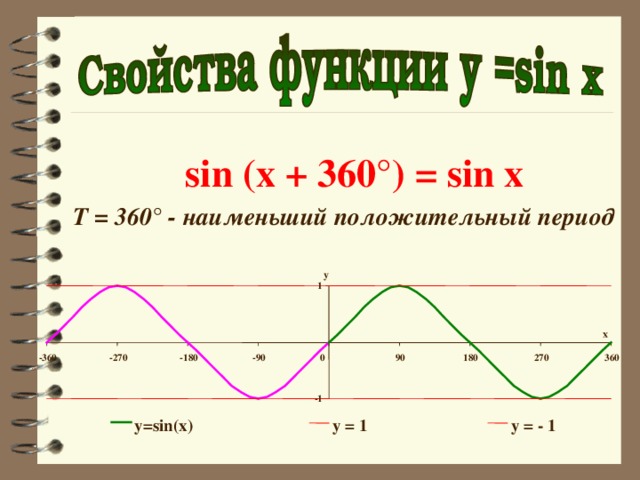
sin (x + 360°) = sin x

T = 360° - наименьший положительный период

y

1

270

360

90

180

0

-90

-180

-270

-360

-1

y=sin(x)

y = 1

y = - 1

x

[ 0; 360°]

функция возрастает от 0 до 1 при 0

функция убывает от 1 до - 1 при 90°

y

1

0

90

180

270

360

-1

x

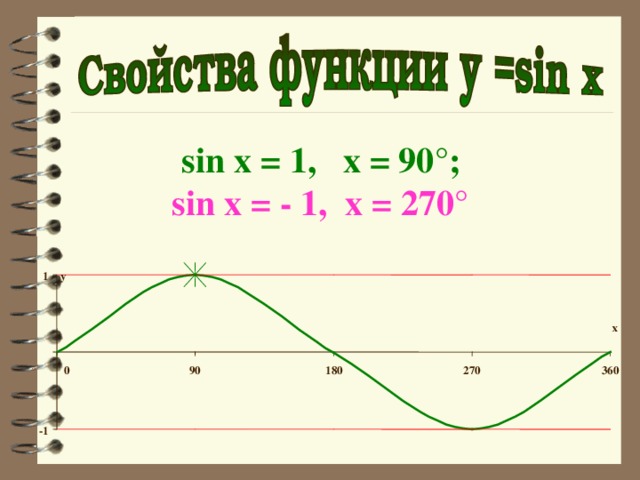
sin x = 1, x = 90°;

sin x = - 1, x = 270°

1

y

0

90

180

270

360

-1

x

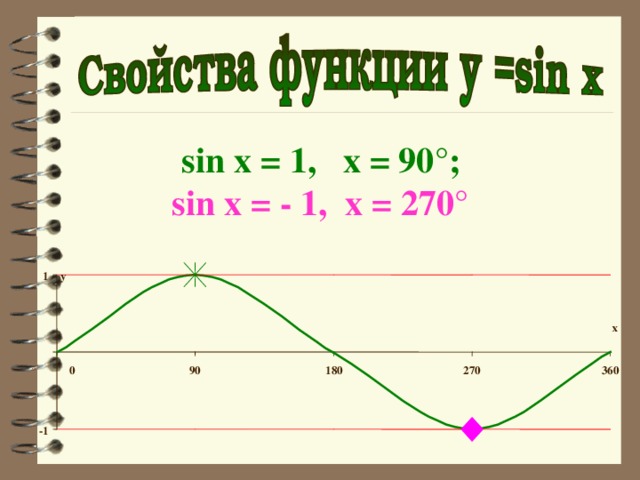
sin x = 1, x = 90°;

sin x = - 1, x = 270°

1

y

0

90

180

270

360

-1

1) D (sin x) = R

2) - 1  sin x  1

3) sin (- x) = - sin x

функция нечетная, график функции симметричен

относительно начала координат

4) sin (x + 360°) = sin x

T = 360° - наименьший положительный период

5) [ 0°; 360°]

функция возрастает от 0 до 1 при 0

функция убывает от 1 до - 1 при 90

6) sin x = 1, x = 90°; sin x = - 1, x = 270°