Презентация "Четные и нечетные функции"

«Рано или поздно всякая правильная математическая идея находит применение в том или ином деле»

11.10

Алгебра - 10

Спирина И.М.

учитель математики МКОУ «Яланская СОШ»

• «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле»

• А.Н. Крылов

Устно:

1. Определение числовой функции.

2. Область определения числовой функции.

3. Область значения числовой функции.

4. График функции.

Устно:

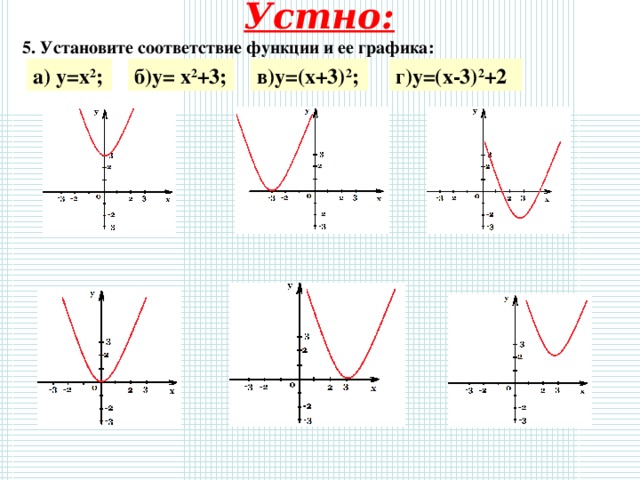
5. Установите соответствие функции и ее графика:

а) у=х 2 ;

б)у= х 2 +3;

г)у=(х-3) 2 +2

в)у=(х+3) 2 ;

• Промежутки, симметричны относительно начала координат, значит для любого х из этого промежутка (-х) также принадлежит этому промежутку.

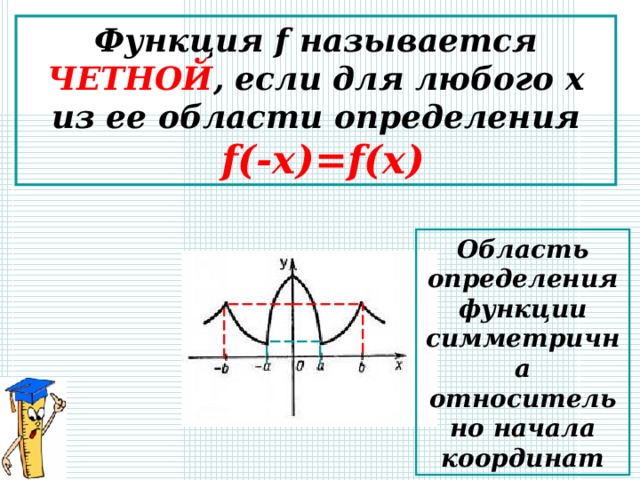
Функция f называется ЧЕТНОЙ , если для любого х из ее области определения

f(-x)=f(x)

Область определения функции симметрична относительно начала координат

Функция f называется НЕЧЕТНОЙ, если для любого х из ее области определения

f(-x)= - f(x)

Область определения функции симметрична относительно начала координат

- a

a

Четность и нечетность тригонометрических функций

Нечетные

функции

Четная

функция

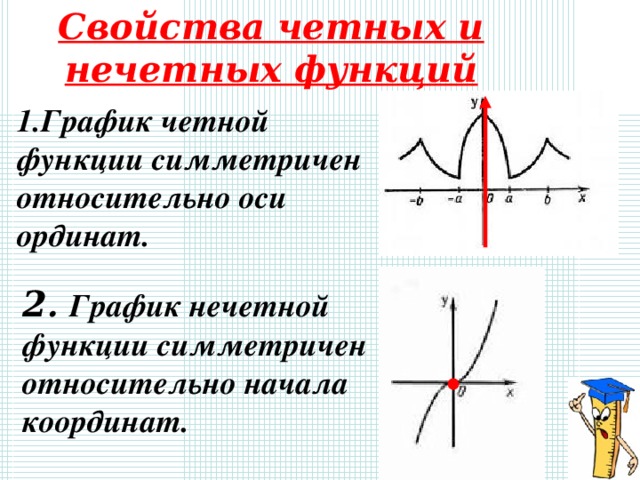
Свойства четных и нечетных функций

• График четной функции симметричен относительно оси ординат.

2 . График нечетной функции симметричен относительно начала координат.

1 . Доказать, что функция f(x ) четная

2. Доказать, что функция g(x ) нечетная

3. Является ли функция f(x ) четной или нечетной?

3 . Докажите, что функции являются четными

3 . Докажите, что функции являются нечетными

Самостоятельная работа

Вариант 2.

Вариант 1.

1. Докажите, что функция f(x)=16х 6 -3х 4  является четной .

2.Приведите пример нечетной функции .

1. Докажите, что функция f(x)=4х 3 +7х является нечетной.

2. Приведите пример четной функции.

Домашнее задание:

п. 4 (1),

№ 58(а), №60 (б), №69(б)

• Оцените свою работу на урок е .
• Удовлетворены ли вы результатом своей работы?