Четные и нечетные функции

Презентация подготовлена в соответствии с учебником под редакцией А. Н. Колмогорова "Алгебра и начала анализа, 10-11", но будет так же полезна и для уроков по другим учебникам.

Функция f называется ЧЕТНОЙ, если для любого х из ее области определения  f(-x)=f(x)

Функция f называется НЕЧЕТНОЙ, если для любого х из ее области определения  f(-x)=-f(x)

СВОЙСТВА

1. График четной функции симметричен относительно оси ординат.

2. График нечетной функции симметричен относительно начала координат.

ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ

Митлаевский А.И.

ГБОУ СОШНО №1975

г. Москва

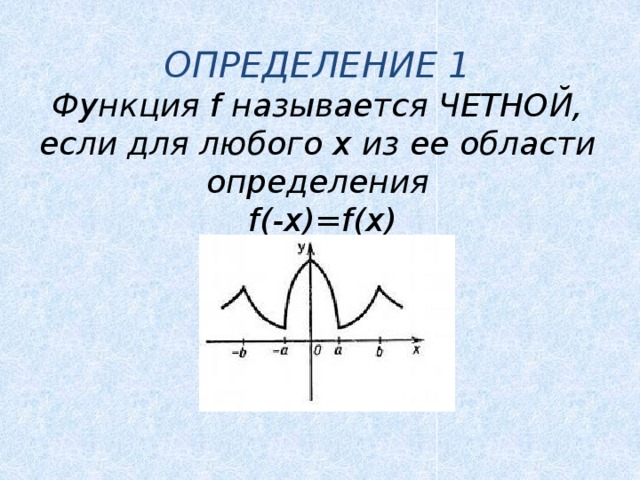
ОПРЕДЕЛЕНИЕ 1

Функция f называется ЧЕТНОЙ, если для любого х из ее области определения

f(-x)=f(x)

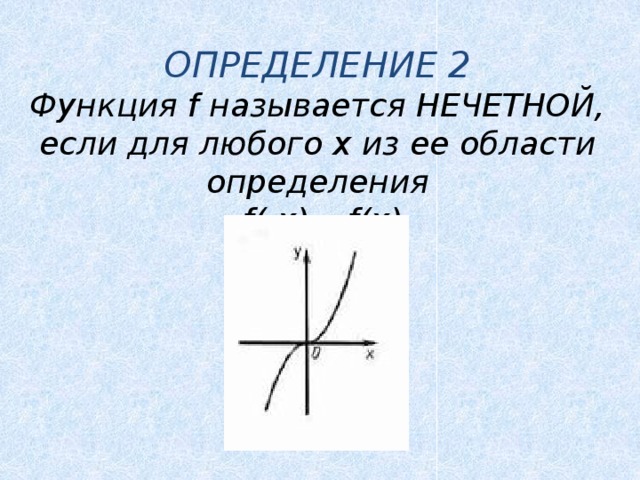
ОПРЕДЕЛЕНИЕ 2

Функция f называется НЕЧЕТНОЙ, если для любого х из ее области определения

f(-x)=-f(x)

СВОЙСТВА

• График четной функции симметричен относительно оси ординат.

• График нечетной функции симметричен относительно начала координат.

ПРИМЕР 1

ПРИМЕР 2

ПРИМЕР 3

ЗАДАНИЕ 1

Докажите, что функции являются четными

ЗАДАНИЕ 2

Докажите, что функции являются нечетными

Использованный материал:

Алгебра и начала анализа, учебник для 10-11 классов, общеобразовательных учреждений,

под редакцией А. Н. Колмогорова.

Использованные картинки:

http://images.yandex.ru/yandsearch?source=wiz&text=%D0%A7%D0%95%D0%A2%D0%9D%D0%AB%D0%95%20%D0%A4%D0%A3%D0%9D%D0%9A%D0%A6%D0%98%D0%98%20%D0%9A%D0%90%D0%A0%D0%A2%D0%98%D0%9D%D0%9A%D0%98&noreask=1&pos=0&rpt=simage&lr=213&uinfo=sw-1263-sh-705-fw-1038-fh-499-pd-1&img_url=http%3A%2F%2F900igr.net%2Fdatai%2Falgebra%2FVozrastanie-i-ubyvanie-funktsii%2F0003-002-Vozrastanie-i-ubyvanie-chetnykh-funktsij.png

http://images.yandex.ru/yandsearch?source=wiz&text=% D0%9D%D0%95%D0%A7%D0%95%D0%A2%D0%9D%D0%AB%D0%95%20%D0%A4%D0%A3%D0%9D%D0%9A%D0%A6%D0%98%D0%98%20%D0%9A%D0%90%D0%A0%D0%A2%D0%98%D0%9D%D0%9A%D0%98&noreask=1&pos=3&rpt=simage&lr=213&uinfo=sw-1263-sh-705-fw-1038-fh-499-pd-1&img_url=http%3A%2F%2Fspravmath.narod.ru%2Fpic%2Fimg002.jpg

http://images.yandex.ru/yandsearch?source=wiz&text=%D0%A7%D0%95%D0%A2%D0%9D%D0%AB%D0%95%20%D0%A4%D0%A3%D0%9D%D0%9A%D0%A6%D0%98%D0%98%20%D0%9A%D0%90%D0%A0%D0%A2%D0%98%D0%9D%D0%9A%D0%98&noreask=1&pos=0&rpt=simage&lr=213&uinfo=sw-1263-sh-705-fw-1038-fh-499-pd-1&img_url=http%3A%2F%2F900igr.net%2Fdatai%2Falgebra%2FVozrastanie-i-ubyvanie-funktsii%2F0003-002-Vozrastanie-i-ubyvanie-chetnykh-funktsij.png