Цель урока:
- обучение быстрому построению графиков функций вида у=f (х+р), у=f(х)+m, у=mf(x), y=f(aх), если известен график функции у=f(х);
- развитие логического мышления при построении и чтении графиков;
- воспитание аккуратности, четкости, грамотности при построении чертежей.
Оборудование: программа для построения графиков «AGrapher», миллиметровая бумага.
Ход урока
I. Организационный момент.
- Мы продолжаем говорить о функциях. Какие вы знаете?
- Сегодня мы поговорим о построении графиков тригонометрических функций.
II. Устная работа.
- Найдите область определения и область значений функций : функций у=соs х, у= sin х.
- Расскажите алгоритм построения графиков функций у=соs (π +х),
- у= - sin (π +х).
- Чем отличаются графики функций у=х2 , у=х2 +2 и у = (х+2)2.
(параболы одинакового вида; они только смещены друг от друга на 2 единицы вдоль оси Оу (второй график) и Ох (третий график).
Можно ли эти свойства применить и для построения тригонометрических функций?
III. Изучение новой темы
1. (Совместная работа c учениками с помощью программы AGrapher)
Построим в одной системе координат графики тригонометрических функций у=sin x, y=sinx + 2, y= sin x - 2.
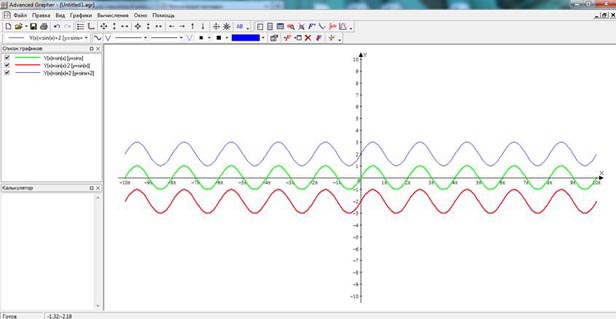
Какой вывод можно сделать?
(Заслушиваются ответы учеников)
Графики тригонометрических функций можно построить путем параллельного переноса на вектор (0;2) график у=sin x, и на вектор (0, - 2) вдоль оси Оу.
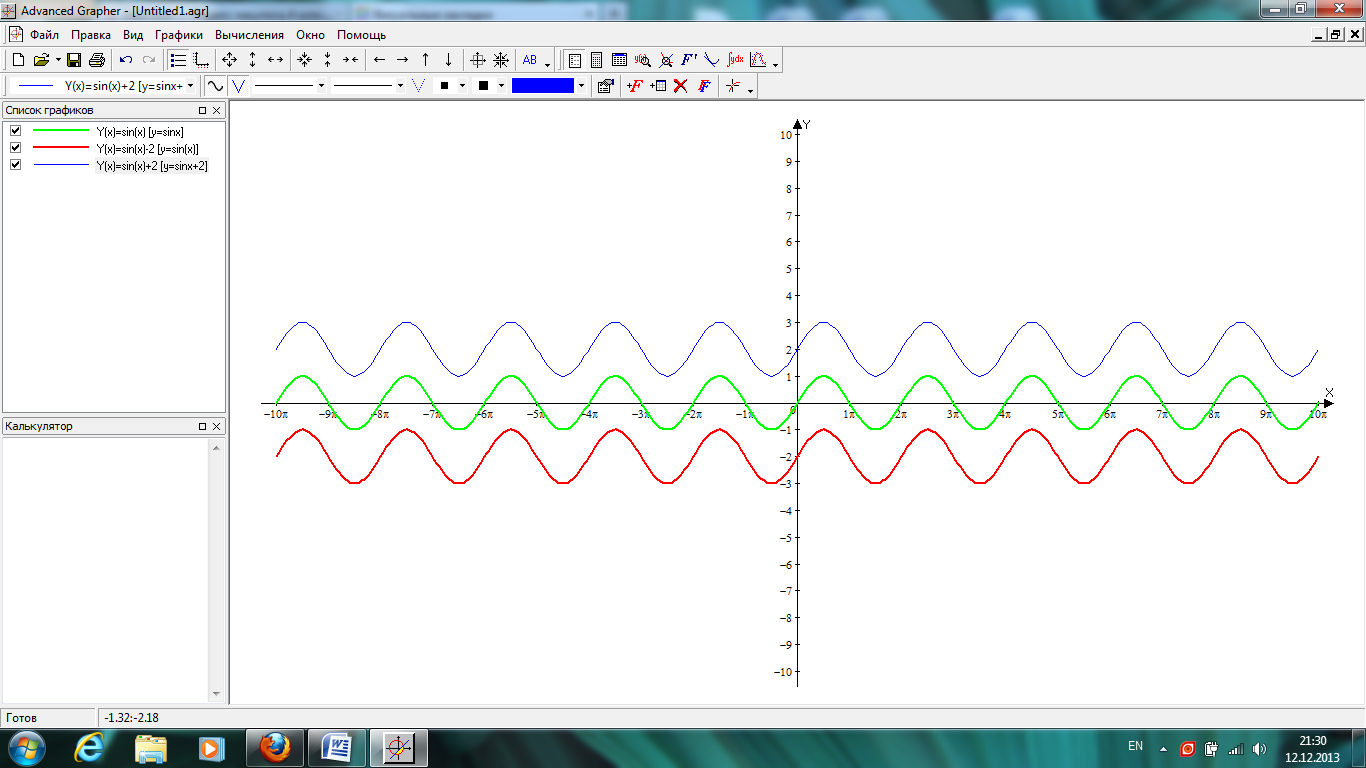
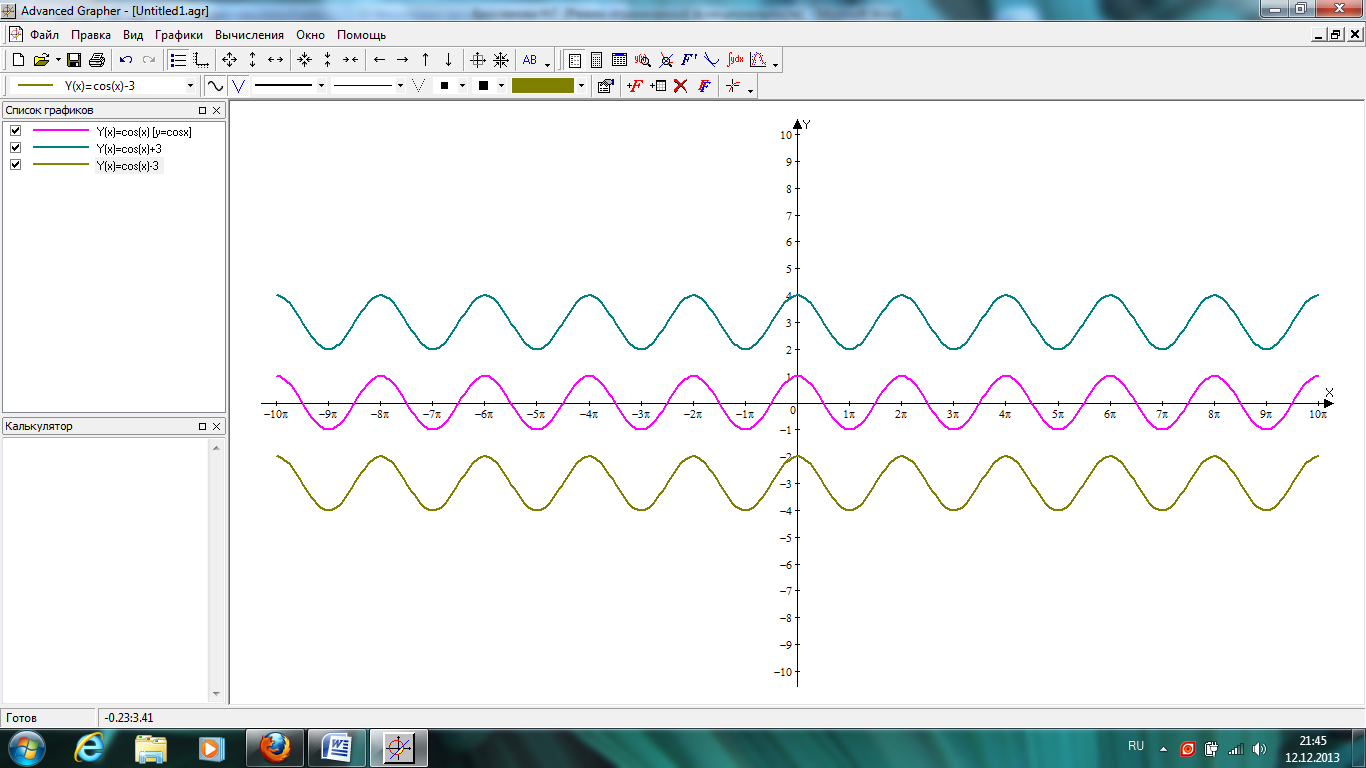
2. Самостоятельно построить графики функций у=сosx, y=cosx+3, y=cosx - 3
Смотрите документ
По окончании работы ученики формулируют правило: чтобы построить график функции у =f(x+p)
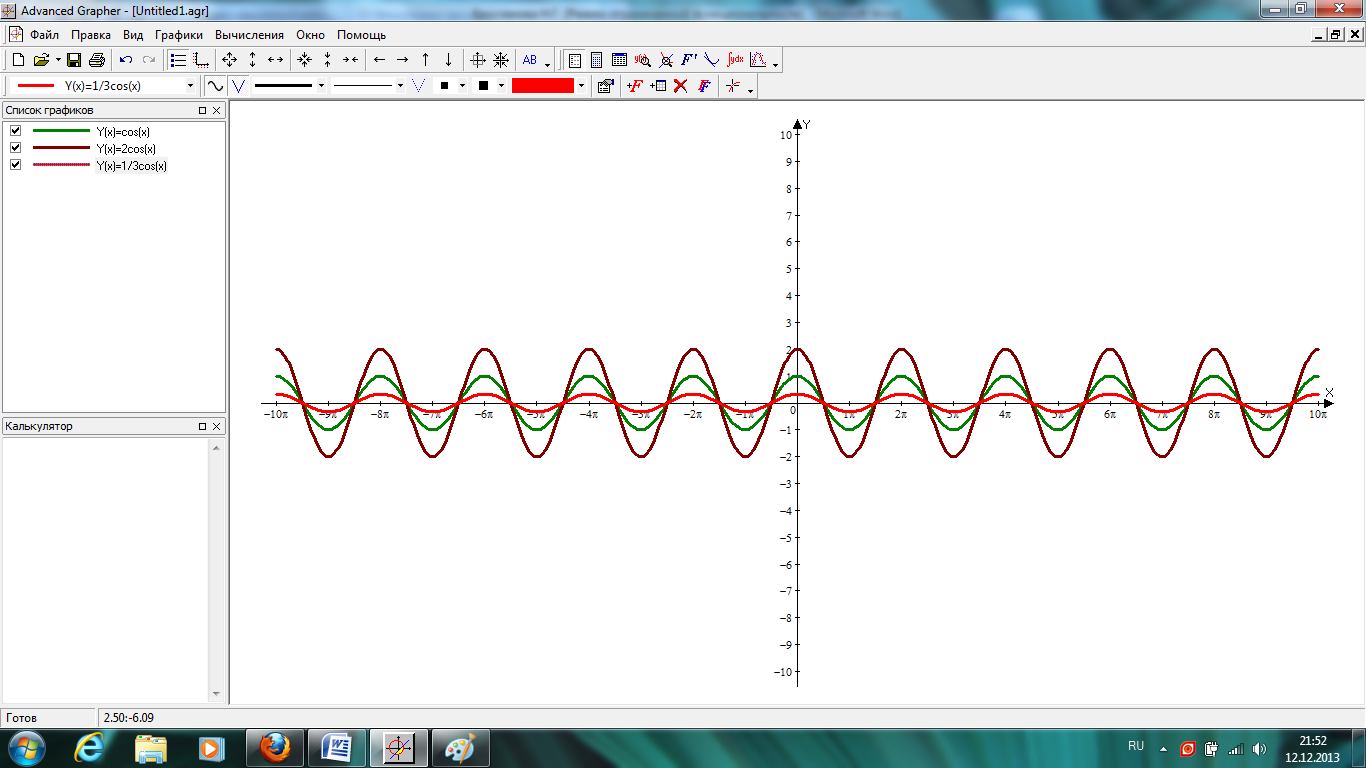
3. Построим следующий вид графиков в одной системе координат: y=cosx, y=1/3cosx, y=2cosx.
Ученики самостоятельно делают вывод.
Для построения графика у=kf(x) надо растянуть график функции у=f(x) в k раз вдоль оси ординат.
Примечание:Если 0<|x|<1, то растяжение с коэффициентом k часто называют сжатием.
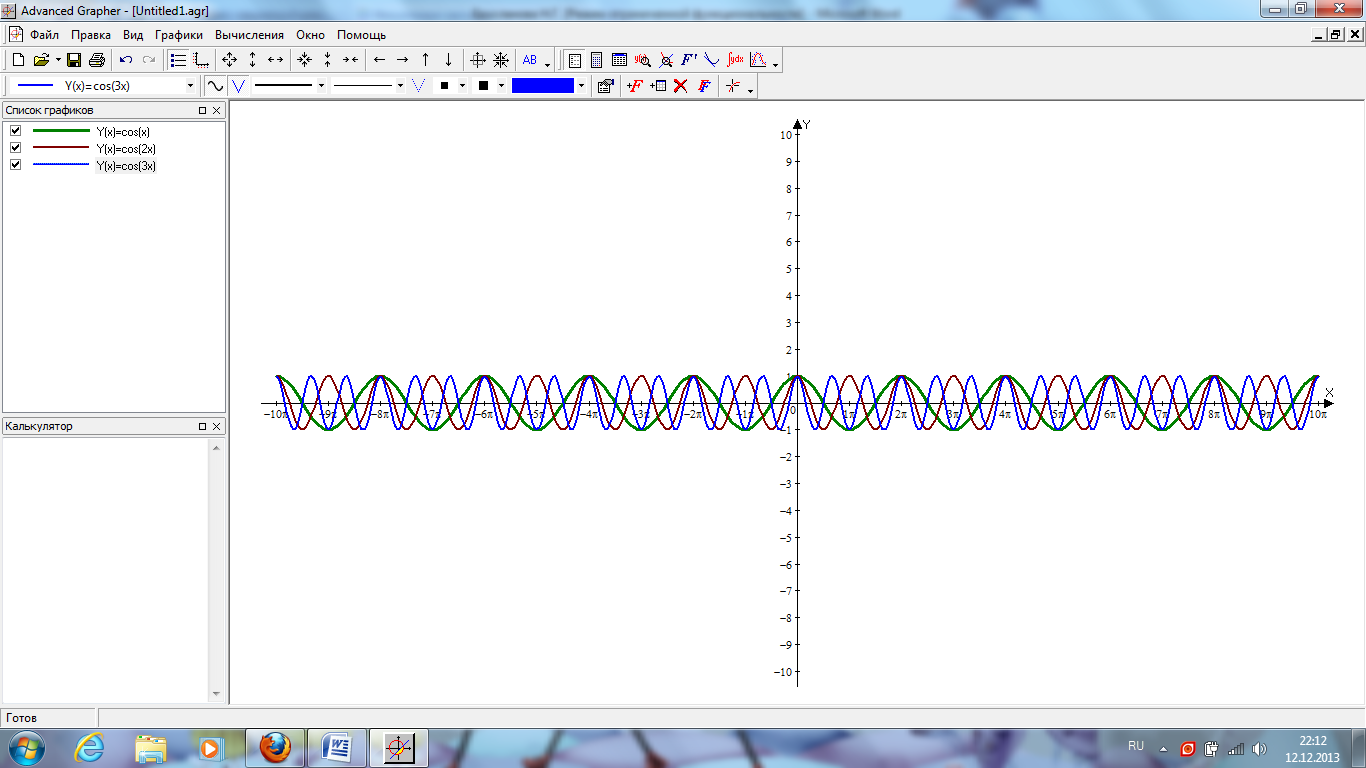
4. Построить графики следующих функций:
y=cos(x), y=cos(2*x) , y=cos(3*x)
Ученики самостоятельно делают вывод.
Для построения графика функции у=f(xk) надо подвергнуть график функции f растяжению с коэффициентом k вдоль оси абсцисс.
IV. Закрепление.
Выполнить в рабочих тетрадях №48 (а, б)
№50 построить на миллиметровой бумаге.
а) у=1+2sinx , б) у=0, 5cosx - 1
Проверить с помощью программы AGrapher
V. Итог
- Повторить алгоритм построения графиков функций
- Оценки
Домашнее задание : №56(а, в), №48(в, г).

 Получите свидетельство
Получите свидетельство Вход
Вход











 Преобразование графиков тригонометрических функций (0.57 MB)
Преобразование графиков тригонометрических функций (0.57 MB)
 0
0 1375
1375 190
190 Нравится
0
Нравится
0


