Построения с помощью циркуля и линейк

Министерство образования и науки Российской Федерации

МУНИУИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНО УЧРЕЖДЕНИЕ

«ГИМНАЗИЯ № 13»

Построения с помощью

циркуля и линейки

(по дисциплине «Геометрия»)

Выполнил: ученик 8 «А» класса

Вишневский Владимир

г. Новомосковск – 2018

Введение

Круг задач, рассматриваемых в геометрии, очень широк. Возможно, самыми древними являются математические задачи на построение. Они привлекли внимание древнегреческих учёных ещё в VI-V веках до нашей эры. Ими занимались почти все крупные греческие геометры: Пифагор и его ученики, Гиппократ, Евклид, Архимед и многие другие. К построениям предъявлялись высокие требования точности, простоты и экономности. Считалось, что самой совершенной линией на плоскости является окружность, а самой простой — прямая. А в школе Платона при решении задач на построение не разрешалось использовать никакие другие инструменты, кроме циркуля и линейки. Такое ограничение сыграло большую роль в развитии геометрии.

Такое противоречие обозначило тему проекта: «Построения с помощью циркуля и линейки».

Предметом изучения являются геометрические задачи на построение с помощью инструментов.

Цель работы –

• закрепить знания по теме «Построения с помощью циркуля и линейки;

• дать представление о новом классе задач на построение.

Исходя из цели, я поставил задачи:

• изучить учебно-методическую литературу на предложенную тему;

• проанализировать и систематизировать полученную информацию;

• привести примеры и решения более сложных задач на построение с помощью циркуля и линейки.

Актуальность проектной работы заключается, во-первых, в том, что геометрические построения должны иметь свое отражение в школьном курсе геометрии в силу недостаточности подготовки учащихся в этой части; во-вторых, высокая степень популярности этих задач возрастает в связи с тем, что находит применение на практике. Умение пользоваться только линейкой и циркулем для решения рассматриваемых в данной работе задач имеет большое значение в практической деятельности.

Практическая значимость данного проекта состоит в использовании его материалов на уроках геометрии и факультативных занятиях по изучению темы «Построения с помощью циркуля и линейки».

Глава 1. Теория

А что же означает понятие построение с помощью циркуля и линейки? Такого термина нет ни в словаре С.И. Ожегова, ни в словаре Д. Н. Ушакова. Но мы можем узнать значения слов: построение, циркуль и линейка, согласно которым мы сможем определить, что же называют построением с помощью данных инструментов. Обратившись к словарю С.И. Ожегова, я узнал, что построение – это вычерчивание геометрических фигур на основании заданных размеров, что циркуль – это инструмент для вычерчивания окружностей, для фиксации длины отрезка с целью измерить или отложить ее в другом месте, а линейка – это простейший измерительный инструмент, как правило, представляющий собой узкую пластину, у которой как минимум одна сторона прямая. Теперь мы можем сказать, что построение с помощью циркуля и линейки — это раздел евклидовой геометрии, известный с античных времён, в котором выполняются построения с помощью двух простейших геометрических инструментов – линейки и циркуля.

Изучив учебную литературу, я выяснил, что решением задачи на построение называется фигура, удовлетворяющая условиям задачи; что найти решение задачи – это значит свести её к конечному числу основных построений, после выполнения которых, искомая фигура будет считаться построенной. Также я узнал, что решение задачи на построение с помощью циркуля и линейки осуществляется в 4-е этапа:

• анализ;

• построение;

• доказательство;

• исследование.

В предложенном проекте мы рассмотрим отдельные этапы построений.

В своей работе я предлагаю вам решения некоторых задач, а именно:

1. Построение правильного шестиугольника.

2. Построение квадрата, вписанного в квадрат.

3. Построение середины оснований трапеции.

4. Построение равностороннего треугольника, описанного около окружности.

5. Построение ромба с углом 45°

Глава 2. Практика

Итак, перейдём от теории к практике.

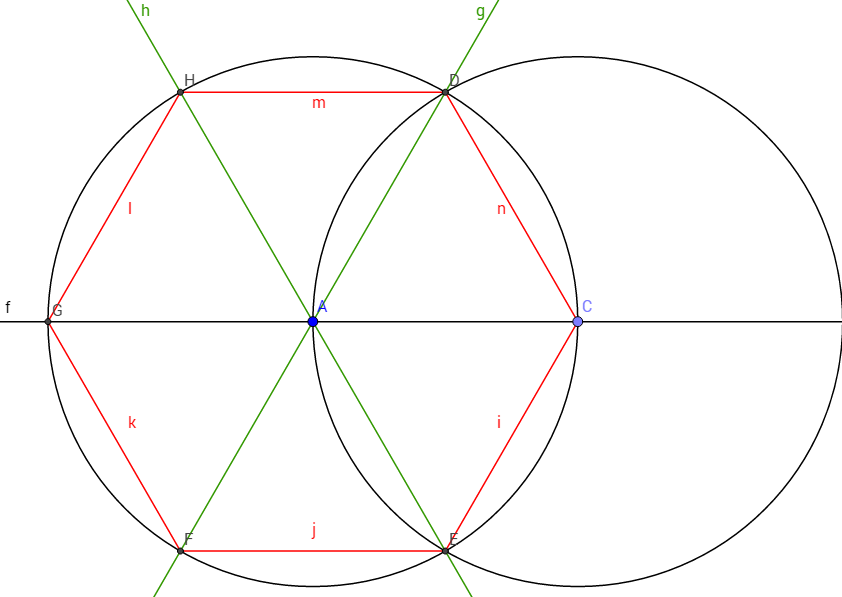
1. Первая задача на построение правильного шестиугольника (Приложение 1):

Для начала надо построить прямую f; затем требуется провести окружность с центром в точке A, чтобы центр окружности лежал на прямой, и окружность пересекала прямую в двух точках. После данных операция надо начертить окружность того же радиуса с центром в точке C, чтобы точка A лежала на окружности, и, проведя прямые h и g, следует соединить все точки в окружности, возникшие при пересечении прямых и окружности (отрезки – HD, DC, CE, EF, FG, GH). Получившаяся фигура – шестиугольник HDCEFG – искомый.

Доказательство: так как мы разделили окружность на шесть равных частей, то и все отрезки, образующие фигуру, равны относительно друг другу.

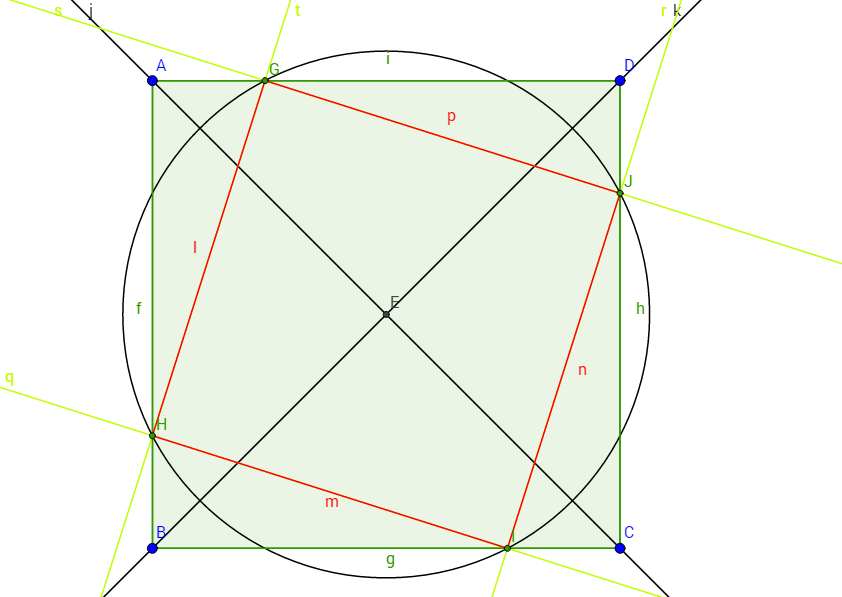
2. Далее я предлагаю вам посмотреть выполнение построения квадрата, вписанного в квадрат (Приложение 2):

Во-первых, начертим квадрат ABCD, во-вторых, найдём центр квадрата, проведя прямые i и k, в-третьих, проведём окружность с центром в точке E, выходящую за пределы квадрата, и соединим точки G, J, I, H, возникшие при пересечении сторон квадрата и окружности (отрезки – GJ, JI, IH, HG). Данное построение, а именно квадрат GJIH, – искомое.

Докажем, что в квадрате образовался квадрат: рассмотрим четыре образовавшихся треугольника – AGH, HIB, JIC и GDJ: так как у квадрата 4 угла – прямых, а также у квадрата все стороны равны, то получившиеся треугольники будут равны (по 1-ому признаку), потому что вписанный квадрат GJIH пересекает стороны квадрата ABCD. Следовательно, внутри квадрата находится вписанный в него квадрат.

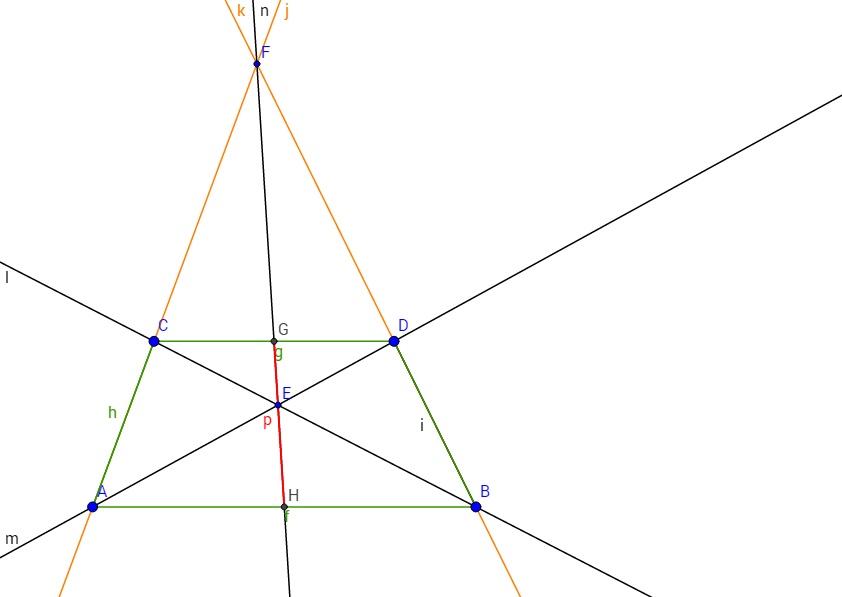
3. Перейдём к третьей задаче (Приложение 3):

Сначала начертим трапецию CDAB, после найдём центр трапеции, проведя две прямые – l и m. Затем продолжим стороны трапеции CA и DB, чтобы получившиеся прямые j и k имели точку пересечения – F, и соединим точку F с точкой E. Исходя из вышеизложенного материала, можно сделать вывод, что точки G и H – искомые (середины оснований трапеции).

Приведём доказательство, оправдывающее наши предположения: возьмём некую трапецию ABCD. Продолжим её боковые стороны до пересечения. Точку пересечения обозначим за F. В треугольнике CDF проведём медиану GF и продолжим её до пересечения с AB. Точку их пересечения обозначим за H.

Треугольники CGF и AFH подобны по 2-м углам (угол CFG – общий, углы FCG и FAH равны, так как являются соответственными), поэтому – FG:FH=CG:AH.

Треугольники FDG и FBH подобны по 2-м углам (угол GFD – общий, углы FDG и FBH равны, так как являются соответственными), поэтому – FG:GH=GD:BH. Поэтому, CG:AH= GD:BH, но CG=DG (по построению), а значит AH=BH, то есть FH является медианой. Таким образом, можно доказать, что медиана FG будет являться медианой для части любой прямой параллельной CD заключённой между прямыми FC, FD. Например, точка E будет серединой прямой o. Заметим, что точки G и H – середины оснований трапеции ABCD.

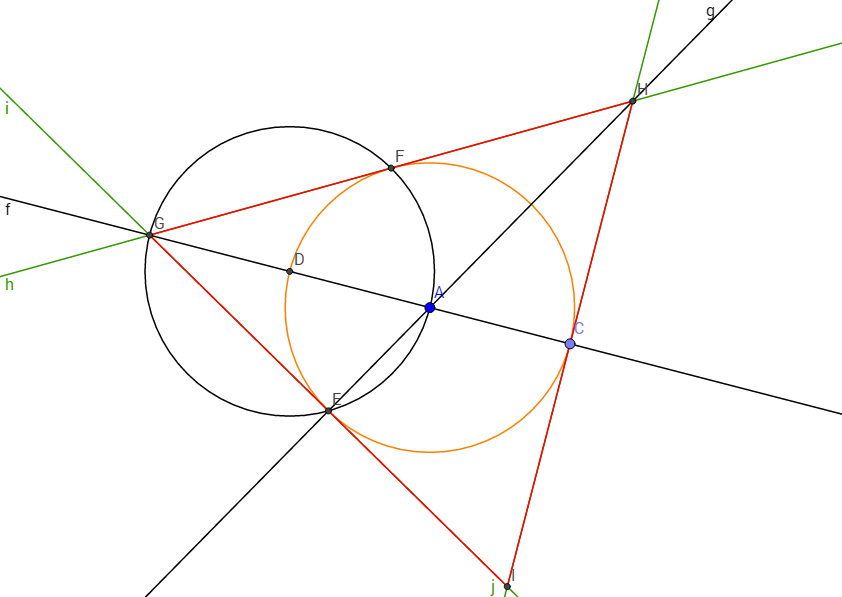
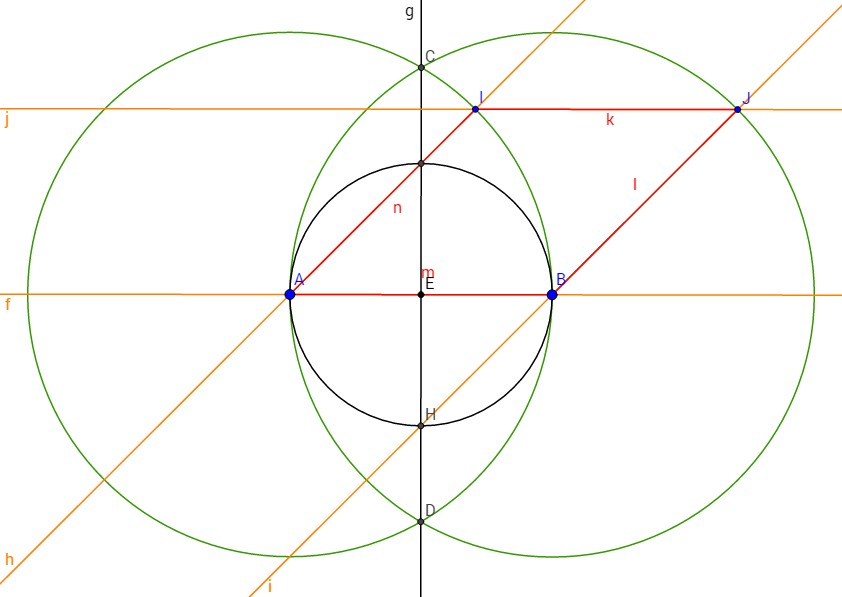
4. Четвёртой задачей является построение равнобедренного треугольника, описанного около окружности (Приложение 4):

Вначале построим окружность в центре с точкой A, после чего построим отрезок AC и прямую f, а также начертим окружность в центре с точкой D, чтобы сторона окружности пересекалась с точкой A. Следом построим прямую g, чтобы она пересекала точки A и E, и построим прямые i и h, чтобы они пересекались в точке G. В конце построим прямую j и соединим точки H и I. Выполненное построение – искомое.

Докажем это. Так как стороны треугольника пересекают сторону окружности, находящейся внутри этого треугольника, всего в трёх точках, то наше построение – верно.

5. Последней задачей будет построение ромба с углом 45° (Приложение 5):

Во-первых, построим отрезок AB и проведём окружность с центром в точке A. Во-вторых, проведём окружность того же радиуса с центром в точке B, чтобы точка A лежала на окружности и построим прямую g, соединив точки C и D. В-третьих, начертим окружность в центре с точкой E, чтобы её стороны соприкасались со сторонами других окружностей, построим прямые h и i, а также соединим точки A, B, J, I. Ромб ABJI – искомый.

Приведём доказательство. Так как у ромба противолежащие углы равны, а известно, что угол IAB = 45°, то и угол IJB = 45°. Следовательно, углы AIJ и JBA равны 135°. Так как сумма углов ромба равна 360°, а наши углы в сумме и дают 360°, то построение выполнено правильно.

Интересные факты

Ещё одним доказательством того, что построения с помощью циркуля и линейки – это важный раздел геометрии, является использование геометрических построений на государственном флаге Ирана, а также разработка и реализация компьютерной игры Euclidea, основанной на построении заданных фигур с помощью циркуля и линейки.

Заключение

В данной итоговой проектной работе рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями с помощью циркуля и линейки.

Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ.

Таким образом, поставленные цели: закрепить знания по теме «Построения с помощью циркуля и линейки»; дать представление о новом классе задач на построение – нами достигнуты. Задачи, предложенные в начале работы, – выполнены.

Здесь нами было использовано практически все четыре этапа: анализ, построение, доказательство и исследование.

Вывод: данная работа может служить учащимся для более глубокого изучения геометрии.

Используемая литература

• Рыжик В.И. Учим математике: теория и практика. 7-11 классы. – М.: ВАКО, 2015. – 240 с. – (Мастерская учителя математики).

• Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 7 класса. – 6-е изд. – М.: Просвещение, 2000. – 128 с.

• Геометрия. 7-9 классы: учеб. для общеобразоват. учреждений / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – 21-е изд. – М.: Просвещение, 2011. – 384 с.

• Википедия. Построение – научная статья: (https://ru.wikipedia.org/wiki/Построение_с_помощью_циркуля_и_линейки)

• Ожегов. С.И Толковый словарь русского языка; 80 000 слов и фразеологических выражений/ Российская академия наук. – 4-е изд., доп. – М.: «А ТЕМП», 2004. – 944 стр.

• Творческая работа по математике. Форум «Учебные материалы»: (http://works.doklad.ru/view/PpS8Vuu78qQ.html)

• Дипломная работа. Автор – Коновалова В.С., г. Киров – 2008: (http://uchit.net/catalog/Pedagogika/137258/#)

Приложение 1

Приложение 2

Приложение 3

Приложение 4

Приложение 5