Цели урока:
- Ввести понятие призмы и её элементов;
- разъяснить понятия: прямая призма, наклонная призма, правильная призма, параллелепипед;
- развивать память, логическое и пространственное мышление, эрудицию, математически и литературно грамотную речь (устную и письменную).
- формировать навыки умственного труда – поиск рациональных путей решения.
Структура урока:
- Организационный момент. Сообщение темы урока.
- Объяснения нового материала.
- Задание на дом.
- Подведение итогов.
Ход урока:
1.) Организационный момент.
Проверка готовности класса к уроку. Сообщение темы и цели урока.
2.) Объяснения нового материала.
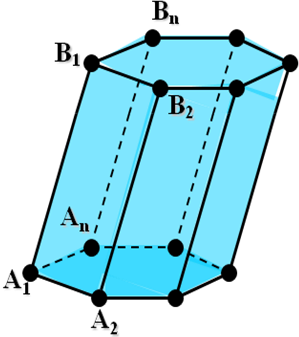
Призмой (n-угольной) называется многогранник, у которого две грани равные n-угольники А1 А2…Аn и В1 В2…В
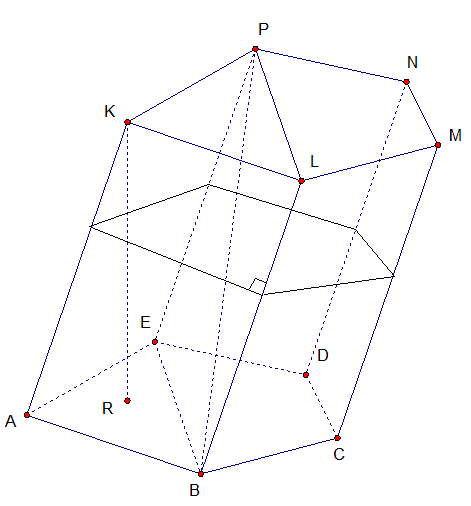
Элементы призмы - смотрите документ
Призма называется прямой, если все её боковые грани являются прямоугольниками.
! Высота прямой призмы равна ее боковому ребру.
Для прямой призмы, у которой боковые ребра перпендикулярны плоскостям оснований, площадь боковой поверхности вычисляется по формуле:
Sбок=PоснH
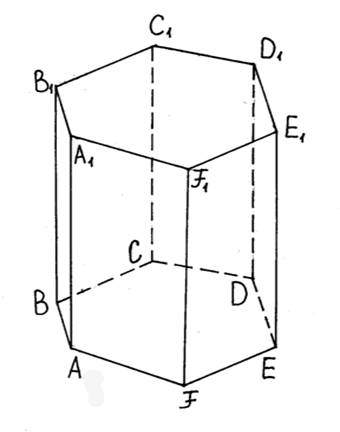
Правильная призма.
Определение: Призма называется правильной, если основаниями её служат правильные многоугольники и боковые рёбра перпендикулярны к основаниям.
В зависимости от числа углов в основании призма называется треугольной, четырёхугольной, пятиугольной и т. д.
Боковыми гранями любой правильной призмы служат прямоугольники.
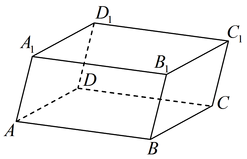
Параллелепипед.
Определение.
Параллелепипед— призма, основаниями которой являются параллелограммы.
Типы параллелепипеда:
Прямоугольный параллелепипед - это параллелепипед, у которого все грани прямоугольники;
Прямой параллелепипед - это параллелепипед, у которого 4 боковые грани прямоугольники;
Куб - это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба - равные квадраты.
Основные элементы:
Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх ребер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями.
Свойства:
Параллелепипед симметричен относительно середины его диагонали.
Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
Противолежащие грани параллелепипеда параллельны и равны.
Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Основные формулы:
Прямой параллелепипед
Площадь боковой поверхности Sбок =Ро*h, где Ро - периметр основания, h - высота
Площадь полной поверхности Sпол =Sб+2Sо, где Sо - площадь основания
Прямоугольный параллелепипед
Площадь боковой поверхности Sбок =2c(a+b),где a, b - стороны основания, c - боковое ребро прямоугольного параллелепипеда
Площадь полной поверхности Sпол=2(ab+bc+ac)
Куб
Площадь боковой поверхности Sбок =4а2
Площадь полной поверхности Sпол =6а2
3). Задание на дом.
§ 1, 2. Ответить на вопросы (приложение 1).
4.) Подведение итогов.
Сегодня на уроке вы познакомились с такими понятиями как: призма, прямая призма, наклонная призма, правильная призма, параллелепипед; Изучили элементы и свойства данных фигур.
Какие у Вас есть ко мне вопросы? Если вопросов нет, спасибо за внимание, до свидание.

 Получите свидетельство
Получите свидетельство Вход
Вход



 араллелепипед.
араллелепипед.








 Понятие многогранника. Призма. Параллелепипед (1.56 MB)
Понятие многогранника. Призма. Параллелепипед (1.56 MB)
 0
0 3044
3044 721
721 Нравится
0
Нравится
0