Понятие цилиндра

1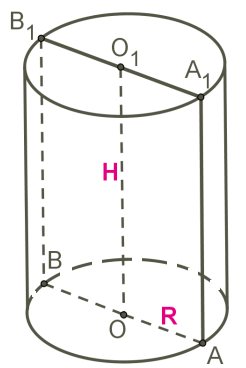 ) Тело, ограниченное ………………………. поверхностью и двумя ………………… с границами L и L₁, называется ……………………...

2) OO₁ - …………………… цилиндра и …………………… цилиндра.
AA₁ - ……………….. цилиндра, длина которой равна длине …………………….. цилиндра.
AO - ……………………. цилиндра.

3) Полученная цилиндрическая поверхность называется  …………………… … ……………….., а круги - ………………………. цилиндра.

4) . …………………………………………………. - это сечение цилиндра плоскостью, которая проходит через ось цилиндра. Это сечение является …………………………………….

5) При сечении цилиндра плоскостью, параллельной оси цилиндра (т.е. перпендикулярной основанию), также получается ……………………………………..

6) При сечении цилиндра плоскостью, параллельной основанию, в сечении получаем ……………….., равный основаниям цилиндра.

7) Так как развёртка - прямоугольник, то боковая поверхность определяется по формуле: ………………

8) Основания цилиндра - два круга с общей площадью …………………...

9) Полная поверхность цилиндра определяется по формуле: ………………………………………..

10) Элементы цилиндра:

• Круги – …………………………;

• цилиндрическая поверхность – …………………………………..;

• прямая ОО₁– ………………………………;

• образующие цилиндрической поверхности – ………………………. цилиндра;

• длина образующей – …………………… цилиндра;

• радиус основания – ……………………… цилиндра.

…………………………………………………………………………………………………………………

1) Тело, ограниченное ………………………. поверхностью и двумя ………………… с границами L и L₁, называется ……………………...

2) Элементы цилиндра:

• Круги – …………………………;

• цилиндрическая поверхность – …………………………………..;

• прямая ОО₁– ………………………………;

• образующие цилиндрической поверхности – ………………………. цилиндра;

• длина образующей – …………………… цилиндра;

• радиус основания – ……………………… цилиндра.

3) Так как развёртка - прямоугольник, то боковая поверхность определяется по формуле: ………………

4) Полученная цилиндрическая поверхность называется  …………………… … ……………….., а круги -  ……………………….  цилиндра.

5) При сечении цилиндра плоскостью, параллельной оси цилиндра (т.е. перпендикулярной основанию), также получается ……………………………………..

6) Основания цилиндра - два круга с общей площадью …………………...

7) При сечении цилиндра плоскостью, параллельной основанию, в сечении получаем ……………….., равный основаниям цилиндра.

8) . …………………………………………………. - это сечение цилиндра плоскостью, которая проходит через ось цилиндра. Это сечение является …………………………………….

9 ) Полная поверхность цилиндра определяется по формуле: ………………………………..

10) OO₁ - …………………… цилиндра и …………………… цилиндра.
AA₁ - ……………….. цилиндра, длина которой равна длине …………………….. цилиндра.
AO - ……………………. цилиндра.