Составила: Бейсембаева Л.К.
Тема: «Показательная функция, её свойства и график»
Цели:
Дидактические:
ввести определение показательной функции;
рассмотреть ее график и свойства при различных а;
сформулировать умение построения графика функции у=ах и умение читать свойства функции по графику.
Развивающие:
развитие познавательного интереса к предмету;
способствовать развитию математической речи, умению наблюдать, сравнивать, делать выводы.
Воспитательные:
продолжить формировать умение правильно воспринимать и активно запоминать новую информацию;
вырабатывать навыки самостоятельной работы.
Тип занятия: изучение нового материала.
Методы обучения: объяснительно-иллюстративный, словесный.
Межпредметные связи: литература. история.
Средства обучения: презентация, учебник, задачник
План занятия
Организационная часть: сообщается тема, а также знания и умения, которыми должны овладеть обучающиеся после изучения данной темы.
Актуализация знаний обучающихся.
2.1. Фронтальный опрос.
- Что такое ап при натуральном п?
- Как определяется степень с целым отрицательным показателем?
- Чему равна нулевая степень числа?
- Как определить аr, где r – рациональное число?
- Как вычислить степень ах при произвольном вещественном х?
- Какие свойства степеней вы знаете?
2.2. Решить устно.
а) 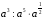 б)
б) 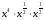 в)
в) 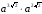 г)
г) 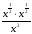 д)
д) 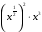
е) 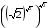 ж)
ж) 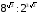 з)
з) 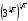
2.3. Работа с графиком (повторить с обучающимися выявление свойств функции по ее графику).
Необходимо найти:
- значения аргумента, при которых значение функции равно нулю;
- координаты точки пересечения с осью ординат;
- значения аргумента, при которых функция принимает положительные (отрицательные) значения;
- промежутки возрастания (убывания) функции.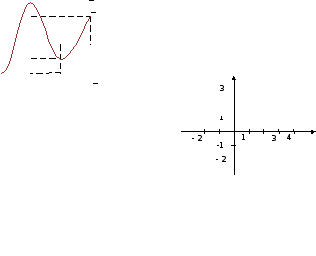
Изучение нового материала.
3.1.Определение показательной функции.
3.2. Перечислить свойства показательной функции.
Закрепление изученного материала.
4.1. Двое обучающихся работают на доске:
1) №449(а; в) и №445(а); 2) №445(а; б) и №450(в).
4.2. Изобразить схематически график функции:
1) 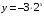 .
.
Сначала строим график функции 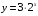 , а затем ему симметричный
, а затем ему симметричный 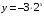 относительно оси ОХ:
относительно оси ОХ:

Если 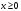 , то
, то 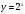 . Поскольку
. Поскольку 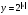 четная функция, то ее график симметричен относительно оси ОУ.
четная функция, то ее график симметричен относительно оси ОУ.

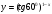 .
.
Так как 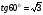 , то запишем данную функцию в виде
, то запишем данную функцию в виде 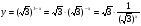 . Здесь
. Здесь 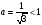 . Значит, функция убывает.
. Значит, функция убывает.
Если х=0, то 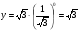 , если х=-1, то
, если х=-1, то .
Творческие задания
Построить графики функций, уравнений или неравенств:
; 2)
; 3)
;
; 5)
; 6)
;
; 8)
.
Указание. Используйте способы преобразования графиков функций и определение модуля.
Итоги занятия, выставление оценок с комментариями.
Домашнее задание:
а) №446(в,г);447(а, б); 450(б); 453(г); 454(г); 455(б,г); 457(б); 458(а,б) – Колмогоров А.Н.
Краткое изложение материала
Функция y = ax, где a – положительное постоянное число, называется показательной функцией.
Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81x имеет при x = 1/4 четыре различных значения: y = 3, y = 3, y = 3 i и y = - 3 i (проверьте, пожалуйста !). Но мы рассматриваем в качестве значения функции только
y=3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.1. Они проходят через точку ( 0, 1 ). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a 1 показательная функция возрастает, a при 0
a
Основные характеристики и свойства показательной функции:
- область определения функции:x (т.e. x
R);
область значений: y0;
- функция монотонна: возрастает при a1 и убывает при 0 a
- функция неограниченная, всюду непрерывная, непериодическая;
- нулей функция не имеет.

 Получите свидетельство
Получите свидетельство Вход
Вход


 б) в) г) д)
б) в) г) д)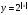









 Показательная функция (147.42 KB)
Показательная функция (147.42 KB)
 0
0 374
374 6
6 Нравится
0
Нравится
0



