Получите свидетельство
Вход
Показательная функция.
Её свойства.
0 , а ≠ 1 0 а 1 а 1 0 а 1 " width="640"
Показательной функцией называется функция вида у=а х ,
где а – некоторое фиксированное положительное число, отличное от 1.
У = а х , где а 0 , а ≠ 1
0 а 1
а 1
0
а
1
0 , а ≠ 1 а 1 0 а 1 Область определения функции : Д(у) = ( - ∞ ;+ ∞ ) Д(у) = ( - ∞ ;+ ∞ ) Множество значений функции : Е(у) = ( 0 ; + ∞) Е(у) = ( 0 ; + ∞) Нули функции : Если х =0, то у = 1 ; а х = 0 - решений нет . Если х =0, то у = 1 ; а х = 0 - решений нет . Участки монотонности : Функция возрастает на всей области определения : ( - ∞ ;+ ∞ ) Функция убывает на всей области определения : ( - ∞ ;+ ∞ ) " width="640"
функции У = а х , где а 0 , а ≠ 1
а 1
0 а 1
Область определения функции :
Д(у) = ( - ∞ ;+ ∞ )
Д(у) = ( - ∞ ;+ ∞ )
Множество значений функции :
Е(у) = ( 0 ; + ∞)
Е(у) = ( 0 ; + ∞)
Нули функции :
Если х =0, то у = 1 ;
а х = 0 - решений нет .
Если х =0, то у = 1 ;
а х = 0 - решений нет .
Участки монотонности :
Функция возрастает на всей области определения : ( - ∞ ;+ ∞ )
Функция убывает на всей области определения : ( - ∞ ;+ ∞ )
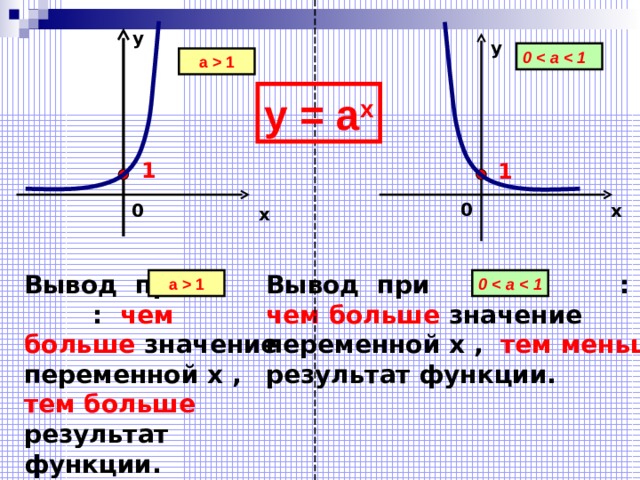1 у = а х 1 1 0 х 0 х Вывод при : чем больше значение переменной х , тем больше результат функции. Вывод при : чем больше значение переменной х , тем меньше результат функции. а 1 0 а 1 " width="640"
у
у
0 а 1
а 1
у = а х
1
1
0
х
0
х
Вывод при : чем больше значение переменной х , тем больше результат функции.
Вывод при :
чем больше значение
переменной х , тем меньше
результат функции.
а 1
0 а 1
а 3/5 ; б) а 7/6 а 11/6 . Желаю удачи!!! " width="640"
Решаю сам .
- Сравните с единицей следующие числа :
а) 0,13 0,5 ; б) 3,7 - 0,4 ; в) (5/7) 0,8 ; г) (2/3) – 1/2 .
2 . Сравните числа :
а) (4/5) 3 и (4/5) 5 ; б) (0,4) -2 и (0,4) 3 ;
в) (2,56) 0 и (0,312) 0 ; г) (1,7) -2 и (1,7) -3 ;
д) (8/5) -3 и (8/5) ½ ; е) (0,2) -6,5 и 5 5,6 .
3.Какие значения может принимать основание показательной функции у = а х , если :
а) а -2/3 а 3/5 ; б) а 7/6 а 11/6 .
Желаю удачи!!!
"Показательная функция" (309 KB)
0
103
11
Нравится
0
