Конспект урока по алгебре и началам анализа в 11классе с углубленным изучением математики
Тема урока: Показательные уравнения
Цель урока:
формировать навыки решения показательных уравнений и уравнений с параметрами;
развивать логическое мышление, память, внимание;
воспитывать культуру математической речи.
Выводы, до которых человек додумывается сам, обычно убеждают его больше, чем те которые пришли в голову другим.
Б. Паскаль
Тип урока: урок формирования и совершенствования новых знаний.
Ход урока.
Мотивация : умение решать показательные уравнения является необходимым умением для успешного усвоения курса математики и поступления в ВУЗ.
1.Актуализация опорных знаний учащихся.
1 Дайте определение простейшего показательного уравнения. В каком случае это уравнение не имеет корней?
2 Какие вы знаете методы решения показательных уравнений?
Обратите внимание на опорный конспект.
| Показательные уравнения 
Если в0 – 1 решение; если  – нет решений. – нет решений.
|
| Сведение к одинаковому основанию | Вынесение общего множителя за скобки | Метод замены переменных | Деление на показательную функцию | Использование свойств функции |
| 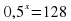
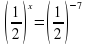
x=-7
| 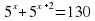



x=1 | 
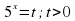



x=0 | 
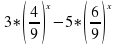 +2=0 +2=0
 +2=0 +2=0
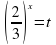
Далее решаем методом замены переменной х=0,х=1. | 
Делим обе части на 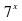 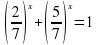
Левая часть – убывающая функция,правая –постоянная,поэтому уравнение имеет один корень. х=1 |
Учащиеся с достаточным и высоким уровнем учебных достижений получают индивидуальные задания, из них 4 ученика выполняют задания на доске . Остальные учащиеся решают устные задания.
Решите уравнения устно.
 =128;
=128;
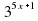 =
= ;
;
 =1;
=1;
 =-1;
=-1;
 =8;
=8;
 +
+ =320;
=320;
 -10*
-10* +16=0.
+16=0.
Задание №1
Решите уравнение
(№19.15 А.Г.Мерзляк Алгебра 11 класс, часть 1, учебник для классов с углубленным изучением математики)
Решение:
Делаем замену: 


Обратная замена:


Ответ:1,5.
Задание № 2
Решите уравнение
(№19.18 А.Г.Мерзляк Алгебра 11 класс часть 1 учебник для классов с углубленным изучением математики)
Решение:
9
Делаем замену:  =t;t0
=t;t0


Обратная замена: 
Ответ:0;2.
Задание № 3
Решите уравнение
(№19.23 А.Г.Мерзляк Алгебра 11 класс часть 1 учебник для классов с углубленным изучением математики)
Решение:
Делаем замену: 
Тогда 
Получаем уравнение: 

Обратная замена 
 или
или 

 ;
;

Ответ: 1;-1.
Задание № 3
Решите уравнение
(№19.31 А.Г.Мерзляк Алгебра 11 класс ,часть 1, учебник для классов с углубленным изучением математики)
Решение.
 t0;
t0;
x в данном случае является параметром.
Возвращаемся к замене:
;
Ответ: 1;3.
2.Работа учащихся под руководством учителя.
Задание № 1
Решите уравнение
 (№19.21 А.Г.Мерзляк Алгебра 11 класс, часть 1, учебник для классов с углубленным изучением математики)
(№19.21 А.Г.Мерзляк Алгебра 11 класс, часть 1, учебник для классов с углубленным изучением математики)
Решение.
;
-замена, тогда, так как


Обратная замена:

Ответ:-2,2.
Задание № 2
При каких значениях параметра а уравнение
имеет единственное решение?
 (№19.24 А.Г.Мерзляк Алгебра 11 класс, часть 1, учебник для классов с углубленным изучением математики)
(№19.24 А.Г.Мерзляк Алгебра 11 класс, часть 1, учебник для классов с углубленным изучением математики)
Решение.
Делаем замену: 

Обратная замена:

Данное уравнение имеет единственный корень, если а-2=1(а=3)
и если а-2≤ 0 (а≤ 2).
Ответ: при а€ .
.
Задание № 3
Решите уравнение 
Решение: Оценим обе части уравнения.
cоs x €  тогда поэтому данное уравнение имеет решение только в том случае, когда левая и правая часть совпадают.
тогда поэтому данное уравнение имеет решение только в том случае, когда левая и правая часть совпадают.

х=0.
Ответ:0.
3.Самостоятельная работа учащихся (тестирование).
Среди заданий самостоятельной работы есть задания, которые встречались во внешнем тестировании.
Вариант №1
| 1.Решите уравнение: 
|
| А | Б | В | Г | Д |
| Нет корней | -0,5 | -1 | 1 | 0,5 |
| 2. Какому из промежутков принадлежит корень уравнения  ? ?
|
| А | Б | В | Г | Д |
| 
| 
| 
| 
| 
|
| 3. Какому из промежутков принадлежит корень уравнения 
|
| А | Б | В | Г | Д |
| 
| 
| 
| 
| 
|
| 4.Найдите сумму корней уравнения  =1 =1
|
| А | Б | В | Г | Д |
| -2 | 0 | 1 | 2 | Нет корней |
| 5.Укажите промежуток которому принадлежит корень уравнения  =39 =39
|
| А | Б | В | Г | Д |
| 
| 
| 
| 
| Другой ответ |
| 6.Решите уравнение |
| Ответ:
|
| 7.Решите уравнение |
| Ответ:
|
| 8.При каких значениях параметра а уравнение имеет единственный корень? |
| Ответ:
|
| 9.Найдите сумму х+у, если пара (х;у) является решением системы уравнений
|
| Ответ:
|
Вариант №2
| 1.Решите уравнение: 
|
| А | Б | В | Г | Д |
| 
| 
| 
| 
| Нет корней |
| 2. Какому из промежутков принадлежит корень уравнения  ? ?
|
| А | Б | В | Г | Д |
| 
| 
| 
| 
| 
|
| 3. Какому из промежутков принадлежит корень уравнения 
|
| А | Б | В | Г | Д |
| 
| 
| 
| 
| 
|
| 4.Найдите произведение корней уравнения  =243 =243
|
| А | Б | В | Г | Д |
| -6 | -4 | 4 | 6 | Нет корней |
| 5.Укажите промежуток которому принадлежит корень уравнения  =651 =651
|
| А | Б | В | Г | Д |
| 
| 
| 
| 
| Другой ответ |
| 6.Решите уравнение |
| Ответ:
|
| 7.Решите уравнение |
| Ответ:
|
| 8.При каких значениях параметра а уравнение не имеет корней? |
| Ответ:
|
| 9.Найдите сумму х+у, если пара (х;у) является решением системы уравнений
|
| Ответ:
|
Задания №1-5 оцениваются 1 баллом,
Задания №6-7 оцениваются 2 баллами,
Задания № 8-9 оцениваются 4 баллами.
Учащиеся могут получить подсказку ,но при этом теряет 1 балл.
4.Подведение итогов урока, оценивание учащихся.
Домашнее задание:
Повторить пункт 19 стр.204-206
I уровень- №19.10(1-3), №19.12
II уровень- №19.16, №19.18(1)
III уровень- №19.22, №19.26, №19.28
Ответы вариант №1
| №1 | №2 | №3 | №4 | №5 |
| Б
| Б | В | Г | Г |
| №6 | №7 | №8 | №9 |
| 
| 
| а€ | 5
|
Ответы вариант №2
| №1 | №2 | №3 | №4 | №5 |
| А
| В | Г | Г | А |
| №6 | №7 | №8 | №9 |
| 3 | -1 | 
| 5
|

 Получите свидетельство
Получите свидетельство Вход
Вход



 – нет решений.
– нет решений.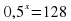
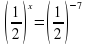
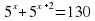




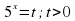




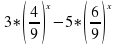 +2=0
+2=0 +2=0
+2=0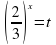

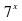
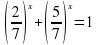
 =128;
=128;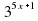 =
= ;
;  =1;
=1;  =-1;
=-1; 








 Показательные уравнения (41.09 КB)
Показательные уравнения (41.09 КB)
 0
0 957
957 86
86 Нравится
0
Нравится
0




