Площадь поверхности пирамиды

ПЛАН УРОКА

Тема урока: Площадь поверхности пирамиды

Цели урока: сформировать понятие боковой и полной поверхности пирамиды

Задачи: закрепить изученный материал в ходе практической работы и решение задач, алгоритм решения задач.

Развития: способствовать развитию пространственного и логического мышления учащихся

Воспитания: вырабатывать в себе самостоятельность настойчивость, уверенность чувство собственного достоинства

Тип урока:Комбинированный; проверка домашнего задания, изложение нового материала. Первичное закрепление изученного

Оборудование набор пирамид

Межпредметные связи

Ход урока

1. Организационный момент. Приветствие. Сообщение темы и задач урока: Сегодня изучаем понятие S боковой и полной поверхности пирамиды, и поверхности правильной пирамиды а также повторяем старый материал, который потребуется для изучения нового.

2. Проверка домашнего задания у доски №

Вопросы учителя:

Чем многогранник отличается от других тел?

Сформулируйте определение многогранника.

Чем пирамида отличается от призмы?

Дайте определение пирамиды.

Назовите основные элементы пирамиды по рисунку (вершина, ребро, грань, основание)

Какая пирамида называется правильной?

Сколько вершин, ребер и граней имеет 4-х,5-ти,10-ти угольные пирамиды?

Какое наименьшее число ребер может быть у многогранника?

какое наименьшее число граней?

Существует ли пирамида, у которой:

А)4 ребра В)11 ребер

Б)6 ребер Г)14 ребер

А теперь давайте посмотрим, что надо сделать, что бы найти площадь поверхности пирамиды. Для этого рассмотрим развертку любой пирамиды и выясним из каких элементов она состоит. Мы видим что Sполн=Sбок+Sосн

Пусть дана правильная n- угольная пирамида где к- длина её апофемы, а-

длина стороны основания Р=ап – периметр основания пирамиды так как S каждого ∆ является боковой гранью S∆=a*k/2 все ∆равны м/у собой и их n штук то S_{бок.пов/пр}.=а*к/2 а так как а*n=Р то S_{бок.пов}=P*k/2 → теорема 5 Площадь боковой поверхности правильной пирамиды равна половине произведения её основания на длину апофемы пирамиды.

S_{бок.пов}=P*k/2

Закрепление.

Для этого чтобы проверить себя каждый из вас берет по одной модели пирамиды, делает необходимые замеры и сделав необходимое оформление задачи находит S полной поверхности пирамиды.

Дано: a= k= N= S_n.n=

Задачи Определите расстояние от вершины правильной треугольной пирамиды до сторон основания если высота пирамиды равна 24 сантиметров, а площадь круга вписанного в основание равна 49 πсм²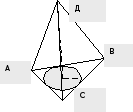

Дано: АВСД – пирамида.

_ΔАВС:

ДО 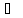АВС

ДО=24

S(O;R)=49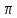см²

ДЕ – апофема

ДЕ - ?

Решение:

_ΔДОЕ: ДЕ²=ДО²+ОЕ²

ОЕ=R радиус вписанной окружности.

S_кр.=πR² →R²=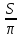==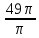49

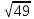ОЕ==7

_ΔДОЕ ДЕ – гипотенуза

ДЕ =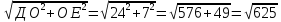

ДЕ=25

Ответ: ДЕ=25

Задача: Сторона основания правильной четырехугольной пирамиды 10 м. высота 12 м. Найдите площадь боковой поверхности

Домашнее задание: Реферат: Пирамида в Казахстане.