Пирамиды

Многогранник, составленный из n-угольника А1А2…Аn и n треугольников А1РА2, А2РА3,…, АnРА1, называется пирамидой. Название «пирамида» происходит от греческого puramiz.

Боковыми гранями пирамиды называются треугольники А1РА2, А2РА3,…, АnРА1, из которых состоит боковая поверхность пирамиды (см. рис.2).

Боковыми ребрами пирамиды называются стороны А1Р, А2Р,… АnР треугольников А1РА2, А2РА3,…, АnРА1 (см. рис.2).

Вершиной пирамиды называется точка Р, в которой сходятся боковые ребра (см. рис.2).

Основанием пирамиды называется многоугольник А1А2… Аn (см. рис.2).

Высотой пирамиды называется перпендикуляр PO, проведенны к плоскости основания из вершины Р (см. рис.2).

Пирамиду обозначают так: РА1 А2… Аn и называют n-угольной пирамидой, где n - число углов основания пирамиды. Так тетраэдр - треугольная пирамида. На рис.1 изображена выпуклая четырехугольная пирамида, а на рис.2 - невыпуклая пятиугольная.

Для определения площади боковой поверхности пирамиды надо найти площади n треугольников и затем сложить их. При вычислении площадей треугольников, образующих боковую поверхность пирамиды, можно использовать все известные формулы площади треугольника.

Площадью полной поверхности пирамиды называется сумма площади боковой поверхности и площади основания.

Формула, по которой вычисляется площадь основания, зависит от формы многоугольника, являющегося основанием пирамиды.

Если рассматривать все возможные углы в пирамиде, то можно выделить 2 вида: плоские углы и двугранные углы, для каждого из которых есть свой линейный угол.

Линейный угол двугранного угла есть пересечение данного двугранного угла и плоскости перпендикулярной его ребру.

Секущей плоскостью тетраэдра называется плоскость, по обе стороны от которой имеются точки этого тетраэдра.

Отрезки, по которым секущая плоскость пересекает грани, называются следами секущей плоскости.

Многоугольник, сторонами которого служат следы, называется сечением тетраэдра данной плоскостью.

Навигация

Автор

Рассмотрим основные действия, которые можно произвести в данной презентации:

Данная кнопка перемещает вас в то место, на которое указывает подсказка, появляющаяся при наведении мыши на кнопку. Кнопка перемещает на несколько пунктов назад.

Данная кнопка перемещает вас в главное содержание презентации. В главное меню вы можете выйти практически с любого слайда.

Данная кнопка перемещает вас также в то место, на которое указывает подсказка, появляющаяся при наведении мыши на кнопку. Кнопка перемещает, как правило, на следующий слайд.

Эта кнопка относится к разделу МЕНЮ или содержанию. Она перемещает вас к определенному разделу работы.

Данный значок обозначает определение или основную мысль части работы, в которой вы находитесь.

Данный значок обозначает мысль, которая прямым образом не относится к части работы , в которой вы находитесь. Он указывает на выражение, которое может быть полезно в других разделах.

Эта кнопка относится к разделу ПРАКТИКА. Она перемещает вас к задаче или тесту, которые указываются при наведении курсора на значок кнопки.

Значение остальных кнопок указывается при наведении на них курсора мыши. Например, эта кнопка запускает программу просмотра 3 d рисунка.

3 d

Цвет кнопок меняется в зависимости оттого, в каком разделе презентации вы находитесь!

!

Любую картинку вы можете просмотреть в увеличенном виде щелкнув по ней кнопкой мыши.

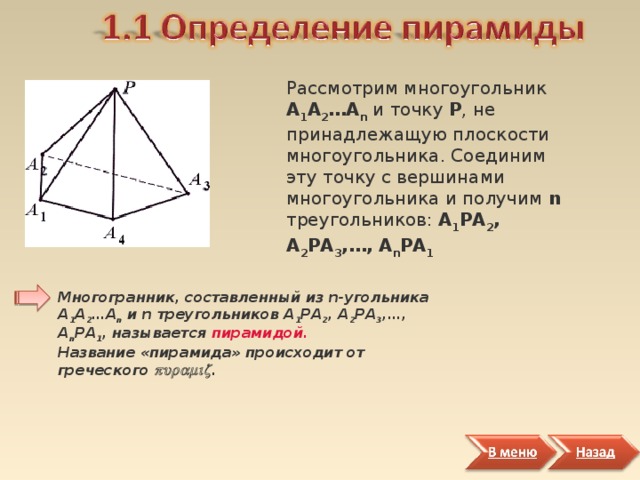
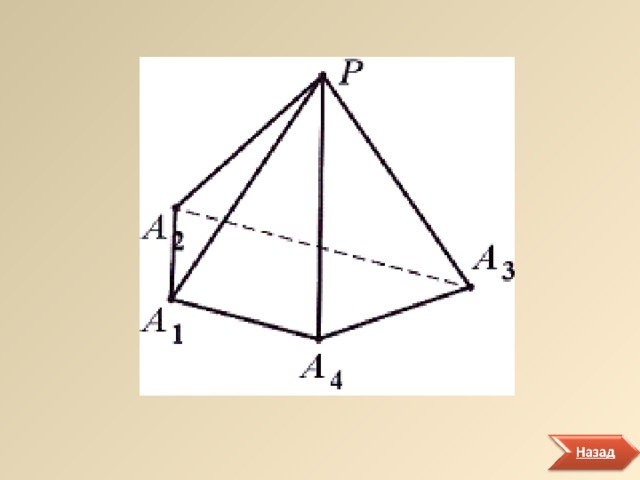
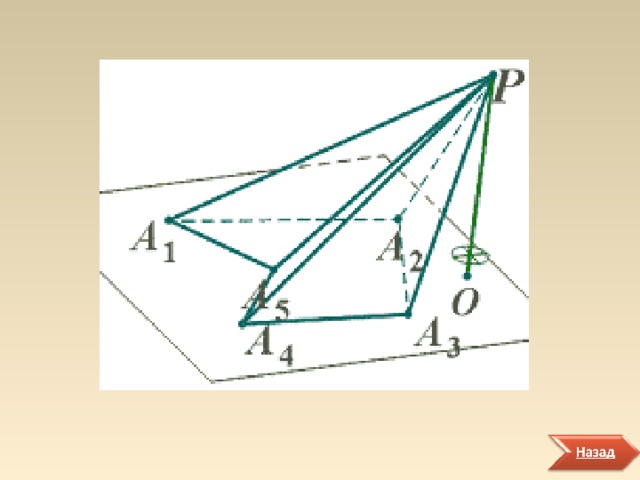
Рассмотрим многоугольник А 1 А 2 … А n и точку Р , не принадлежащую плоскости многоугольника. Соединим эту точку с вершинами многоугольника и получим n треугольников: А 1 РА 2 , А 2 РА 3 , … , А n РА 1

Многогранник, составленный из n-угольника А 1 А 2 …А n и n треугольников А 1 РА 2 , А 2 РА 3 ,…, А n РА 1 , называется пирамидой. Название «пирамида» происходит от греческого  .

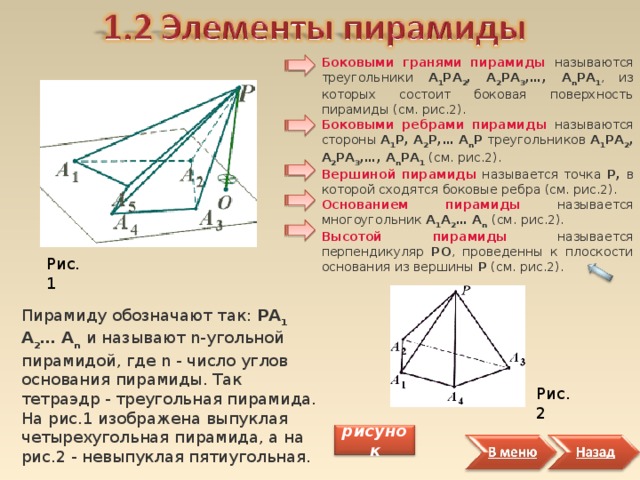
Боковыми гранями пирамиды называются треугольники А 1 РА 2 , А 2 РА 3 , … , А n РА 1 , из которых состоит боковая поверхность пирамиды (см. рис.2).

Боковыми ребрами пирамиды называются стороны А 1 Р, А 2 Р, … А n Р треугольников А 1 РА 2 , А 2 РА 3 , … , А n РА 1 (см. рис.2).

Вершиной пирамиды называется точка Р, в которой сходятся боковые ребра (см. рис.2).

Основанием пирамиды называется многоугольник А 1 А 2 … А n (см. рис.2).

Высотой пирамиды называется перпендикуляр PO , проведенны к плоскости основания из вершины Р (см. рис.2).

Рис.1

Пирамиду обозначают так: РА 1 А 2 … А n и называют n-угольной пирамидой, где n - число углов основания пирамиды. Так тетраэдр - треугольная пирамида. На рис.1 изображена выпуклая четырехугольная пирамида, а на рис.2 - невыпуклая пятиугольная.

Рис.2

рисунок

Для определения площади боковой поверхности пирамиды надо найти площади n треугольников и затем сложить их.При вычислении площадей треугольников, образующих боковую поверхность пирамиды, можно использовать все известные формулы площади треугольника.

Площадью полной поверхности пирамиды называется сумма площади боковой поверхности и площади основания :

Площадью боковой поверхности пирамиды называется сумма площадей боковых граней пирамиды. Каждая из боковых граней - треугольник. Поэтому ее площадь равна полупроизведению основания на высоту . Основанием треугольника будет соответствующая сторона основания пирамиды, а высотой треугольника - высота соответствующей боковой грани, обозначенная на рисунке как l 1 , l 2 , … Тогда площадь боковой поверхности пирамиды определится по формуле:

Формула, по которой вычисляется площадь основания, зависит от формы многоугольника, являющегося основанием пирамиды.

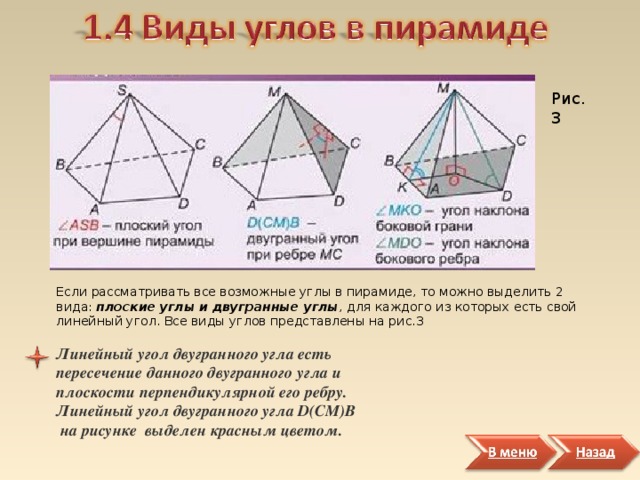
Рис.3

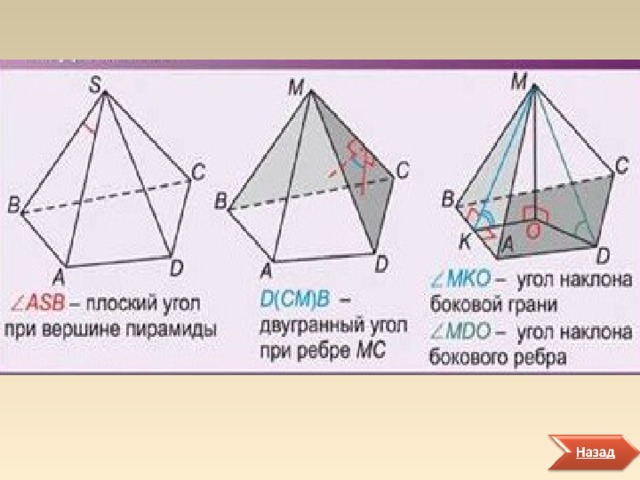
Если рассматривать все возможные углы в пирамиде, то можно выделить 2 вида: плоские углы и двугранные углы , для каждого из которых есть свой линейный угол. Все виды углов представлены на рис.3

Линейный угол двугранного угла есть пересечение данного двугранного угла и плоскости перпендикулярной его ребру. Линейный угол двугранного угла D ( CM ) B на рисунке выделен красным цветом.

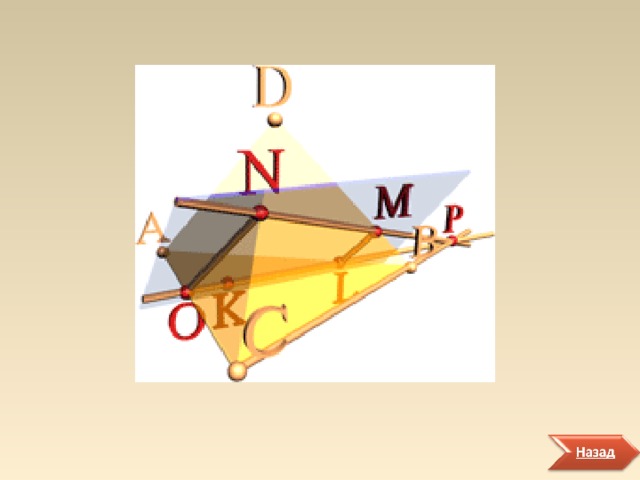
Секущей плоскостью тетраэдра называется плоскость, по обе стороны от которой имеются точки этого тетраэдра.

Отрезки, по которым секущая плоскость пересекает грани, называются следами секущей плоскости .

Многоугольник, сторонами которого служат следы, называется сечением тетраэдра данной плоскостью.

На рисунке секущей плоскостью тетраэдра ABCD является плоскость PNК .Следы представлены отрезками NO,OL,LM,MN . Сечением является четырехугольник LMNO.

3 d

3 d

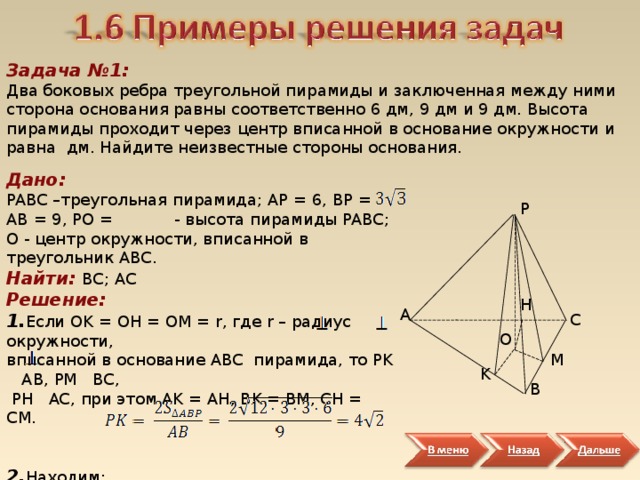
Задача №1:

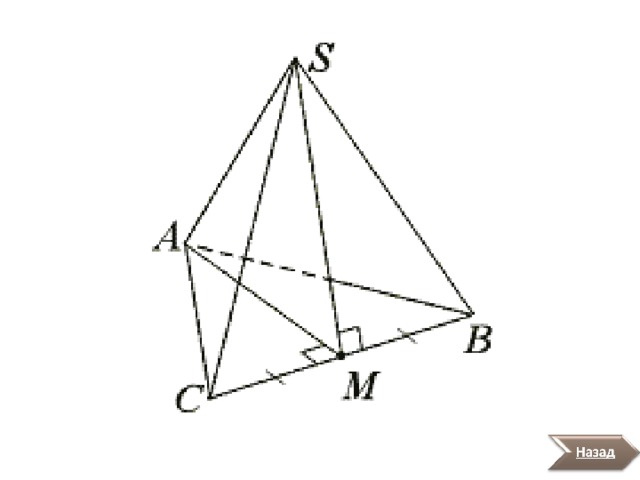
Два боковых ребра треугольной пирамиды и заключенная между ними сторона основания равны соответственно 6 дм, 9 дм и 9 дм. Высота пирамиды проходит через центр вписанной в основание окружности и равна дм. Найдите неизвестные стороны основания.

Дано:

PABC –треугольная пирамида; AP = 6, BP = AB = 9, PO = - высота пирамиды PABC ; О - центр окружности, вписанной в треугольник ABC .

Найти: BC ; AC

Решение:

1. Если OK = OH = OM = r , где r – радиус окружности,

вписанной в основание ABC пирамида, то PK AB , PM BC ,

PH AC , при этом AK = AH , BK = BM , CH = CM .

2. Находим:

P

H

A

C

O

M

K

B

3. Тогда , значит, AH = 7 и BK = 2. Кроме

того , .

4. Если CM = CH = х , то периметр треугольника ABC равен 2  (9 + х ), а его площадь

равна . Это означает, что

т.е. 5( х + 9) = 14 х , откуда х = 5. Тогда BC = 7, AC = 12.

Ответ: BC = 7, AC = 12.

А теперь попробуем закрепить полученные знания! Удачи!

1А. У четырехугольной пирамиды сумма числа граней и ребер равна:

• Восьми Десяти Тринадцати Двенадцати
• Восьми
• Десяти
• Тринадцати
• Двенадцати

2А. У пятиугольной пирамиды разность числа ребер и вершин равна:

• Трем Четырем Нулю Двум
• Трем
• Четырем
• Нулю
• Двум

3А. У шестиугольной пирамиды произведение числа вершин на число

граней равно:

• Двадцати Четырем Сорока девяти Тридцати шести
• Двадцати
• Четырем
• Сорока девяти
• Тридцати шести

4a. При сечении треугольной пирамиды плоскостью сечение

представляет собой:

• Только треугольники Только четырехугольники Треугольники и четырехугольники Треугольники и пятиугольники
• Только треугольники
• Только четырехугольники
• Треугольники и четырехугольники
• Треугольники и пятиугольники

5Б. Сечение четырехугольной пирамиды плоскостью, проходящей через

середины трех боковых ребер – это:

• Треугольник, параллельный основанию Четырехугольник, параллельный основанию Треугольник, непараллельный основанию Четырехугольник, непараллельный основанию
• Треугольник, параллельный основанию
• Четырехугольник, параллельный основанию
• Треугольник, непараллельный основанию
• Четырехугольник, непараллельный основанию

6Б. У треугольной пирамиды прямоугольным треугольником может быть:

• Только одна грань От одной до 4-х граней От одной до 3-х граней От одной до 2-х граней
• Только одна грань
• От одной до 4-х граней
• От одной до 3-х граней
• От одной до 2-х граней

7С. Секущая плоскость, проходящая через середины трех боковых ребер пирамиды, делит пирамиду на два многогранника, площади боковых поверхностей которых относятся как:

• 1:4 2:3 1:3 1:2
• 1:4
• 2:3
• 1:3
• 1:2

8С. Куб можно разбить нa n четырехугольных пирамид с основаниями и высотами, равными основанию и высоте куба. При этом n равно:

• 4 2 3 5
• 4
• 2
• 3
• 5

Треугольники АВС, ABD, ACD, BCD , из которых состоит поверхность тетраэдра, называются гранями тетраэдра .

Стороны треугольников, образующих поверхность тетраэдра, называются ребрами тетраэдра .

Точки A,B,C,D , в которых сходятся ребра, называются вершинами .

Всего тетраэдр имеет 4 грани, 6 ребер и 4 вершины.

Название « тетраэдр » происходит от греческих слов tetra (четыре) и hedron (грань). То есть данный многогранник назван по количеству граней, образующих его поверхность.

Одну из граней тетраэдра (любую) можно назвать основанием тетраэдра , а остальные грани по отношению к ней — боковыми.

Ребра, не принадлежащие одной плоскости, называют скрещивающимися . Например, ребра AD и BC.

Пусть точки A,B,C,D не лежат в одной плоскости. Поверхность, образованная треугольниками АВС, ABD, ACD, BCD, называется тетраэдром ABCD.

3 d

Боковые ребра пирамиды равны тогда и только тогда, когда: 1) около основания можно описать окружность; 2)   вершина пирамиды проектируется в центр этой окружности

Доказательство

Докажем необходимость. 1 . Пусть около основания можно описать окружность и вершина пирамиды проектируется в центр этой окружности. 2. Докажем, что при этих условиях боковые ребра пирамиды равны.

3. Поскольку O - центр описанной окружности, то ОА 1 = ОА 2 = … ОА n =R (радиусы описанной окружности). В то же время ОА 1 , ОА 2 , … ОА n - проекции наклонных SA 1 , SA 2 , … SA n . Наклонные равны друг другу, поскольку равны их проекции. Необходимость доказана.

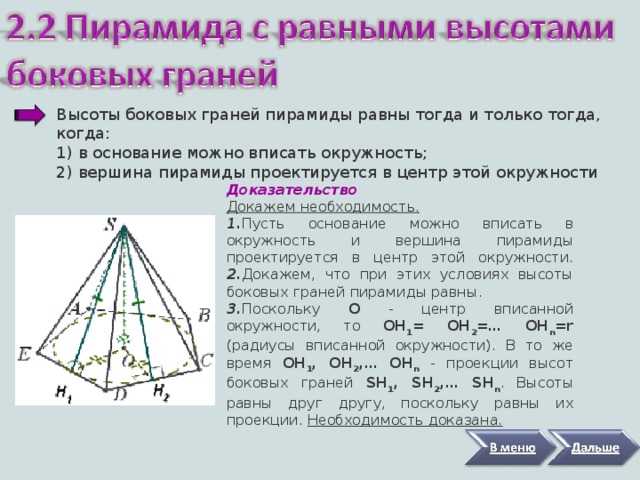
Высоты боковых граней пирамиды равны тогда и только тогда, когда:

1) в основание можно вписать окружность; 2) вершина пирамиды проектируется в центр этой окружности

Доказательство

Докажем необходимость.

1. Пусть основание можно вписать в окружность и вершина пирамиды проектируется в центр этой окружности. 2. Докажем, что при этих условиях высоты боковых граней пирамиды равны.

3. Поскольку O - центр вписанной окружности, то ОH 1 = ОH 2 = … ОH n =r (радиусы вписанной окружности). В то же время ОН 1 , ОН 2 , … ОН n - проекции высот боковых граней SН 1 , SН 2 , … SН n . Высоты равны друг другу, поскольку равны их проекции. Необходимость доказана.

Доказательство

Докажем достаточность.

1. Пусть высоты боковых граней пирамиды равны.

2. Докажем, что при этом условии в основание пирамиды можно вписать окружность и вершина пирамиды проектируется в центр этой окружности. Для этого достаточно доказать, что точка О равноудалена от точек Н 1 , Н 2 , … Н n .

3. Поскольку высоты боковых граней равны друг другу, то равны и их проекции ОН 1 = ОН 2 = … ОН n . Поскольку высоты перпендикулярны сторонам основания, то и их проекции перпендикулярны соответствующим сторонам основания (по обратной теореме о трех перпендикулярах - урок 11). Но тогда точка О , являясь проекцией вершины S на плоскость основания, равноудалена от сторон многоугольника АBCD … и, следовательно, является центром окружности, вписанной в этот многоугольник. Достаточность доказана.

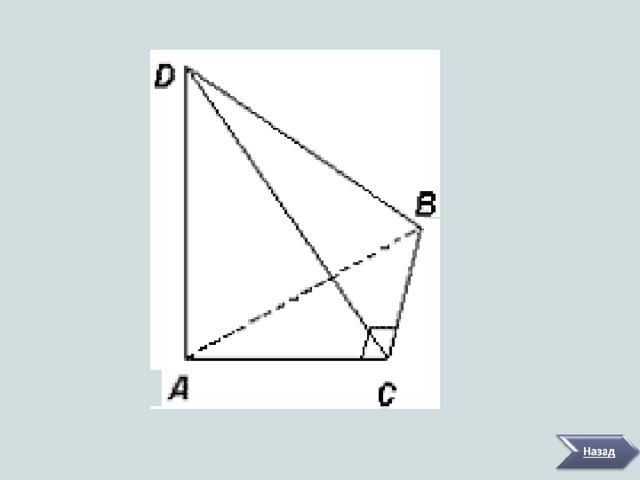
Рассмотрим пирамиду, у которой в основании прямоугольный треугольник, а одно из боковых ребер перпендикулярно основанию и опирается на вершину острого угла этого треугольника. Такую пирамиду иногда называют биортогональной. На рисунке Δ АВС - прямоугольный, ∠С=90 0 , AD ⊥(ABC). Поэтому AD - высота пирамиды.

Особенностью этой пирамиды является то, что все ее грани - прямоугольные треугольники. В самом деле, Δ АВС - прямоугольный по условию, Δ DAС и Δ DAВ - прямоугольные, т.к. AD ⊥(ABC) и, следовательно AD ⊥AB и AD ⊥AC (по определению прямой, перпендикулярной плоскости) и наконец Δ DСВ - прямоугольный, т.к. DС ⊥ВC (по теореме о трех перпендикулярах).

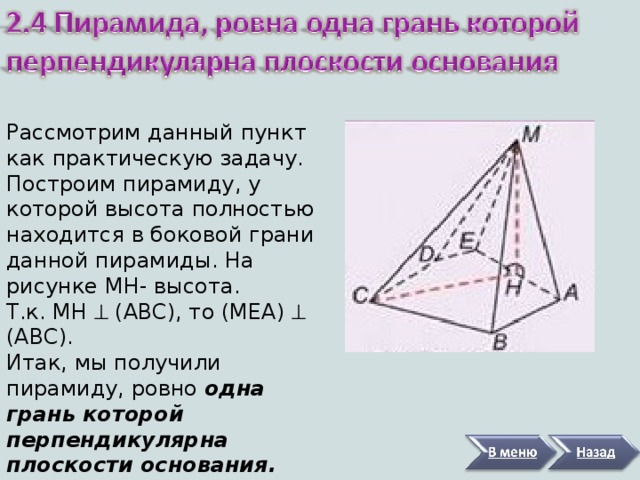
Рассмотрим данный пункт как практическую задачу.

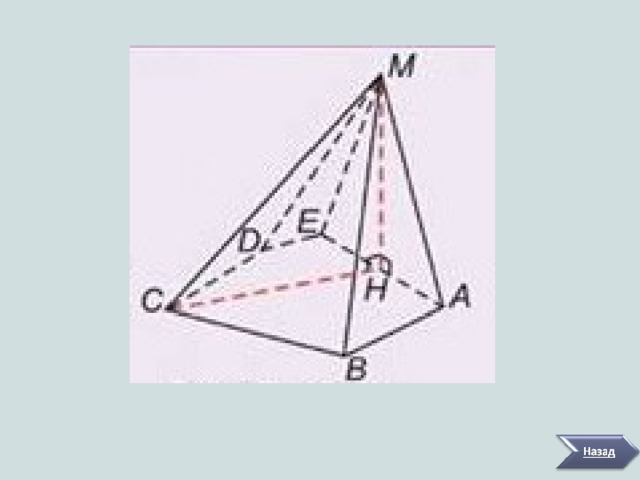
Построим пирамиду, у которой высота полностью находится в боковой грани данной пирамиды. На рисунке MH- высота.

Т.к. MH  (ABC) , то ( MEA )  (ABC) .

Итак, мы получили пирамиду, ровно одна грань которой перпендикулярна плоскости основания.

Р

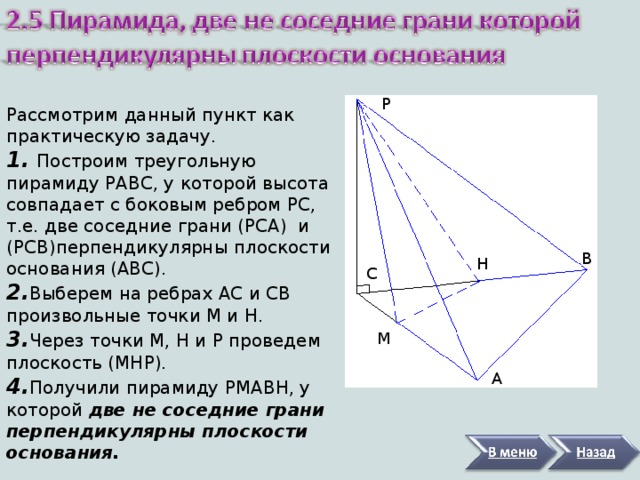
Рассмотрим данный пункт как практическую задачу.

1. Построим треугольную пирамиду РАВС, у которой высота совпадает с боковым ребром РС, т.е. две соседние грани (РСА) и (РСВ)перпендикулярны плоскости основания (АВС).

2. Выберем на ребрах АС и СВ произвольные точки М и Н.

3. Через точки М, Н и Р проведем плоскость (МНР).

4. Получили пирамиду РМАВН, у которой две не соседние грани перпендикулярны плоскости основания.

В

Н

С

М

А

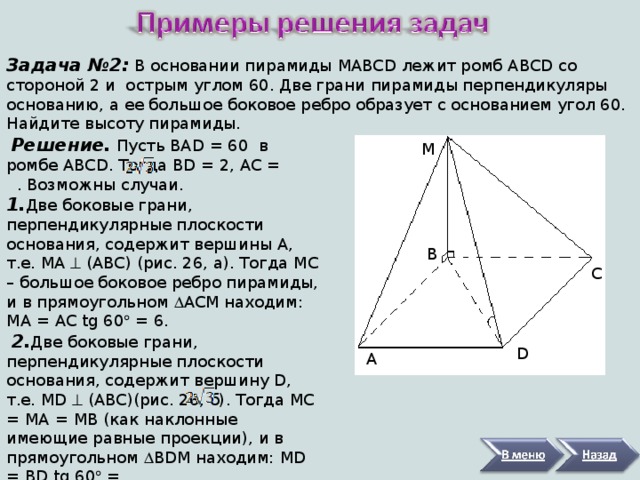
Задача №2: В основании пирамиды MABCD лежит ромб ABCD со стороной 2 и острым углом 60. Две грани пирамиды перпендикуляры основанию, а ее большое боковое ребро образует с основанием угол 60. Найдите высоту пирамиды.

Решение. Пусть BAD = 60 в ромбе ABCD . Тогда BD = 2, AC = . Возможны случаи.

1. Две боковые грани, перпендикулярные плоскости основания, содержит вершины A , т.е. MA  ( ABC ) (рис. 26, а). Тогда MC – большое боковое ребро пирамиды, и в прямоугольном  ACM находим: MA = AC tg 60  = 6.

2. Две боковые грани, перпендикулярные плоскости основания, содержит вершину D , т.е. MD  ( ABC )(рис. 26, б). Тогда MC = MA = MB (как наклонные имеющие равные проекции), и в прямоугольном  BDM находим: MD = BD tg 60  = .

М

В

С

D

А

1А. Боковые ребра пирамиды равны тогда и только тогда, когда:

• В основание можно вписать окружность, а вершина пирамиды проектируется в центр этой окружности Около основания можно описать окружность В основание пирамиды можно вписать окружность Около основания можно описать окружность, а вершина пирамиды проектируется в центр этой окружности
• В основание можно вписать окружность, а вершина пирамиды проектируется в центр этой окружности
• Около основания можно описать окружность
• В основание пирамиды можно вписать окружность
• Около основания можно описать окружность, а вершина пирамиды проектируется в центр этой окружности

2А. Высоты боковых граней пирамиды равны тогда и только тогда, когда:

• В основание можно вписать окружность, а вершина пирамиды проектируется в центр этой окружности Около основания можно описать окружность Вершина пирамиды проектируется в центр этой окружности Около основания можно описать окружность, а вершина пирамиды проектируется в центр этой окружности
• В основание можно вписать окружность, а вершина пирамиды проектируется в центр этой окружности
• Около основания можно описать окружность
• Вершина пирамиды проектируется в центр этой окружности
• Около основания можно описать окружность, а вершина пирамиды проектируется в центр этой окружности

3А. У четырехугольной пирамиды число ребер в два раза меньше:

• Шестнадцати Восьми Десяти Двенадцати
• Шестнадцати
• Восьми
• Десяти
• Двенадцати

4А. У пятиугольной пирамиды число вершин и число граней относятся как:

• 3:1 2:1 1:1 1:2
• 3:1
• 2:1
• 1:1
• 1:2

5А. При сечении четырехугольной пирамиды плоскостью сечение

представляет собой n – угольник, где:

• n=3 n=4 3 ≤ n ≤ 4 3 ≤ n ≤ 5
• n=3
• n=4
• 3 ≤ n ≤ 4
• 3 ≤ n ≤ 5

6А. У шестиугольной пирамиды число вершин плюс число ребер минус

удвоенное число граней равно:

• 0 7 -2 5
• 0
• 7
• -2
• 5

7Б. Боковые ребра пирамиды равны тогда и только тогда, когда:

• В основание пирамиды можно вписать окружность Около основания можно описать окружность, а вершина пирамиды проектируется в центр этой окружности В основание можно вписать окружность, а вершина пирамиды проектируется в центр этой окружности Около основания можно описать окружность
• В основание пирамиды можно вписать окружность
• Около основания можно описать окружность, а вершина пирамиды проектируется в центр этой окружности
• В основание можно вписать окружность, а вершина пирамиды проектируется в центр этой окружности
• Около основания можно описать окружность

8Б. Сечение четырехугольной пирамиды плоскостью, проходящей через

середины трех ребер, имеющих общую вершину, это n-угольник, где:

• n=3 n=4 n=3, n=4 или n=6 3 ≤ n ≤ 5
• n=3
• n=4
• n=3, n=4 или n=6
• 3 ≤ n ≤ 5

9Б. Если в основании пирамиды прямоугольный треугольник, а две

боковые грани, содержащие стороны острого угла этого треугольника,

перпендикулярны основанию, то:

• 4 грани пирамиды – прямоугольные треугольники 3 грани пирамиды – прямоугольные треугольники 2 грани пирамиды – прямоугольные треугольники 1 грань пирамиды – прямоугольный треугольник
• 4 грани пирамиды – прямоугольные треугольники
• 3 грани пирамиды – прямоугольные треугольники
• 2 грани пирамиды – прямоугольные треугольники
• 1 грань пирамиды – прямоугольный треугольник

8С. Секущая плоскость, проходящая через середины трех боковых ребер

пирамиды, делит любую боковую грань на фигуры, площади которых

относятся как:

• 1:3 2:3 1:4 1:2
• 1:3
• 2:3
• 1:4
• 1:2

9С. Через вершины четырехугольной пирамиды можно провести N пар

скрещивающихся прямых, где N равно:

• 12 9 6 8
• 12
• 9
• 6
• 8

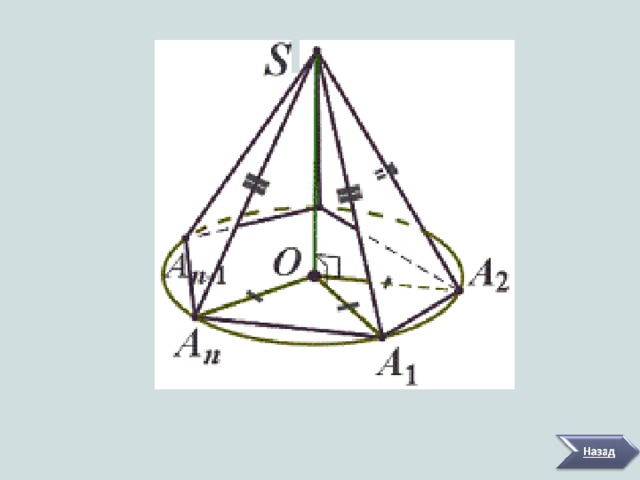
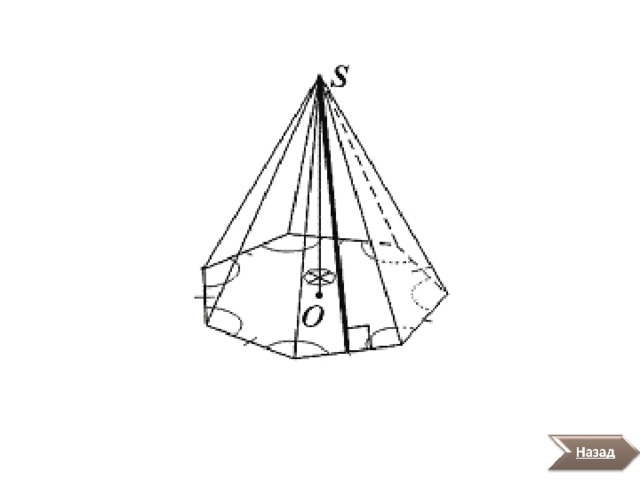
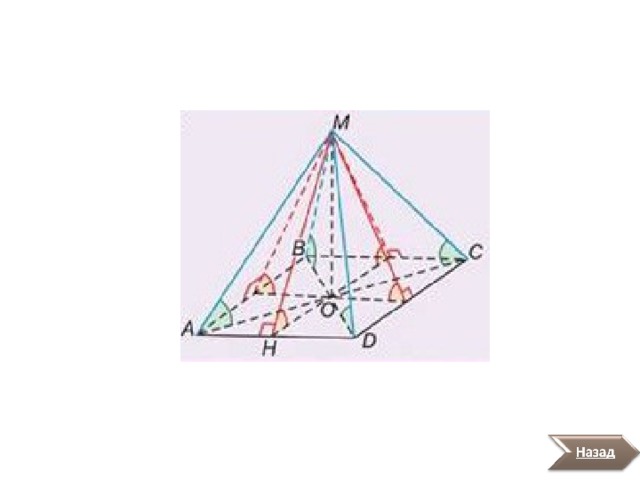
Пирамида называется правильной, если ее основанием является правильный многоугольник, а вершина проектируется в центр основания.

Поскольку вокруг правильного многоугольника можно описать окружность, а вершина правильной пирамиды проектируется в центр основания, то боковые ребра пирамиды равны друг другу (см. теорему о пирамиде с равными боковыми ребрами). Следовательно, грани правильной пирамиды - равнобедренные треугольники. Высоты боковых граней пирамиды, проведенные из ее вершины, называются апофемами. Аналогично доказывается то, что высоты боковых граней пирамиды равны друг другу (см. теорему о пирамиде с равными высотами). Следовательно, апофемы равны друг другу.

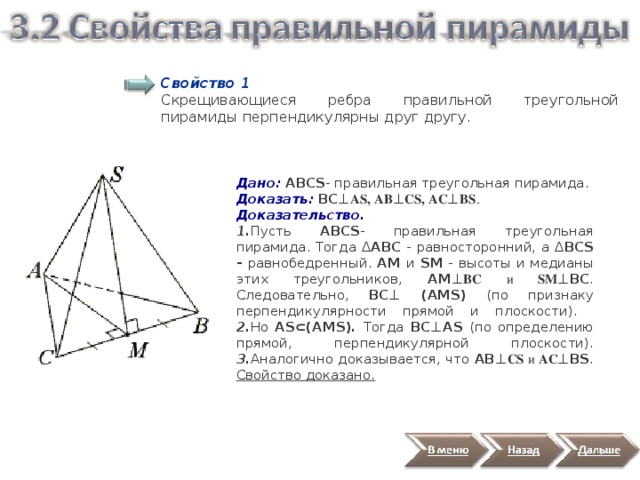
Свойство 1

Скрещивающиеся ребра правильной треугольной пирамиды перпендикулярны друг другу.

Дано: ABCS - правильная треугольная пирамида.

Доказать: BC ⊥ AS, АB ⊥ СS, АC ⊥ ВS .

Доказательство.

1. Пусть ABCS - правильная треугольная пирамида. Тогда Δ АВС - равносторонний, а Δ ВСS - равнобедренный. AМ и SM - высоты и медианы этих треугольников, AМ ⊥ BC и SM ⊥BC . Следовательно, ВС ⊥ (AMS) (по признаку перпендикулярности прямой и плоскости). 2. Но AS ⊂(AMS). Тогда BC ⊥AS (по определению прямой, перпендикулярной плоскости). 3. Аналогично доказывается, что АB ⊥ СS и АC ⊥ВS .

Свойство доказано.

Свойство 2

Плоскость, проведенная через боковое ребро и высоту правильной треугольной пирамиды, перпендикулярна ребру основания и содержащей его боковой грани.

Дано: ABCS - правильная треугольная пирамида.

Доказать: (AMS) ⊥ BC, (AMS) ⊥ (BCS) .

Доказательство.

1. Пусть ABCS - правильная треугольная пирамида. Тогда АВС - равносторонний, а ВСS - равнобедренный. AМ и SM - высоты и медианы этих треугольников, AМ ⊥BC и SM ⊥BC . Следовательно, ВС ⊥(AMS) (по признаку перпендикулярности прямой и плоскости). 2. Тогда (AMS) ⊥(BCS) (по признаку перпендикулярности плоскостей).

Свойство доказано.

Просмотреть рисунок

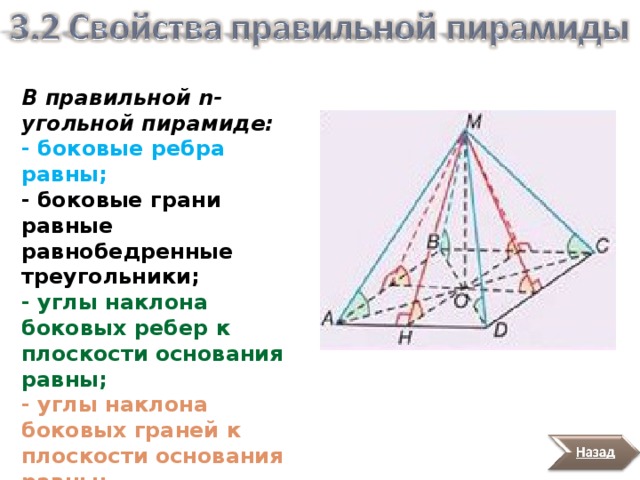
В правильной n -угольной пирамиде:

- боковые ребра равны;

- боковые грани равные равнобедренные треугольники;

- углы наклона боковых ребер к плоскости основания равны;

- углы наклона боковых граней к плоскости основания равны;

- апофемы равны.

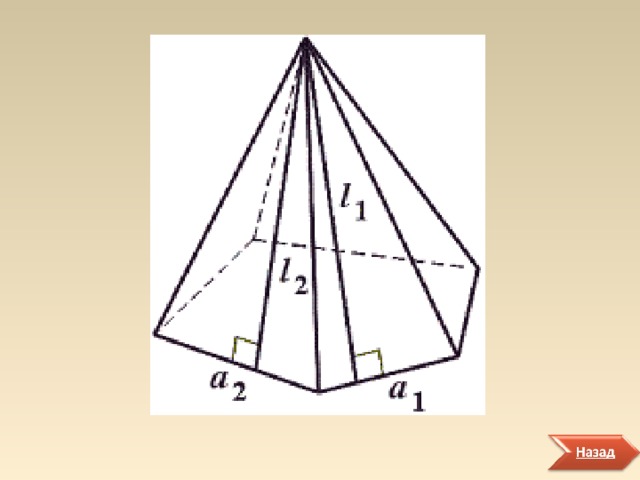
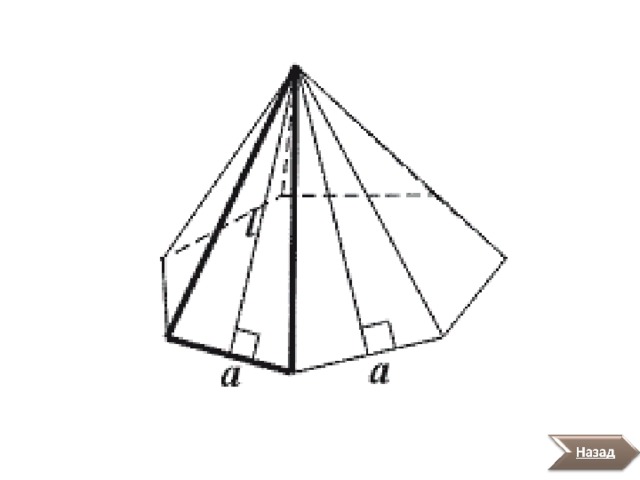
Площадь боковой поверхности правильной пирамиды равна произведению полупериметра ее основания на апофему.

Дано: р -полупериметр основания; l -апофема.

Доказать: S бок =pl .

Доказательство.

1. Пусть сторона основания равна а . Каждая боковая грань - треугольник. Поэтому ее площадь определяется по формуле S гр =0,5al .

2. Боковая поверхность правильной пирамиды состоит из n равных треугольников. Тогда ее площадь S бок =0,5nal=pl .

Теорема доказана.

Замечание . Полученная формула справедлива для любой пирамиды, у которой боковые грани имеют равные высоты. С учетом теоремы о пирамиде с равными высотами боковых граней можно утверждать, что эта формула справедлива для всех пирамид, в основание которых можно вписать окружность, а вершина пирамиды проектируется в центр этой окружности.

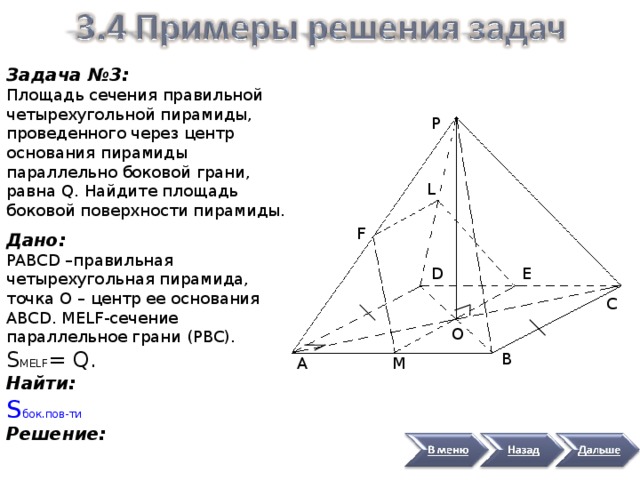
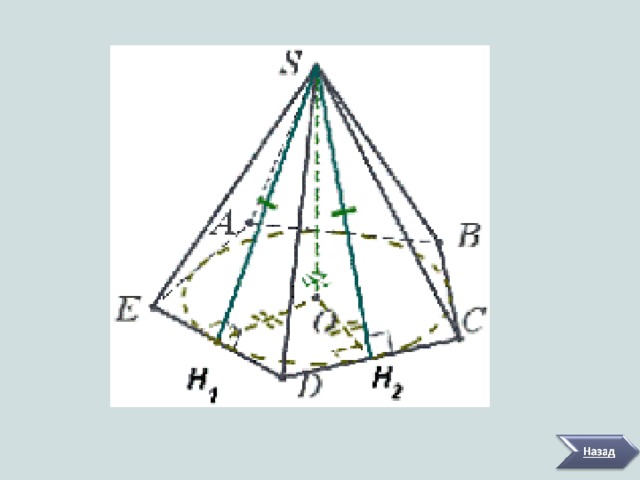
Задача №3:

Площадь сечения правильной четырехугольной пирамиды, проведенного через центр основания пирамиды параллельно боковой грани, равна Q . Найдите площадь боковой поверхности пирамиды.

Р

L

F

Дано:

PABCD –правильная четырехугольная пирамида, точка O – центр ее основания ABCD . MELF- сечение параллельное грани ( PBC ). S MELF = Q .

Найти:

S бок.пов-ти

Решение:

D

Е

С

O

В

А

М

1. Если сечение пирамиды параллельно грани PBC , а точки M и E – середины соответственно AB и CD , то это сечение представляет собой равнобедренную трапецию, одним основанием которой служит отрезок ME , а другим – отрезок FL ║ ME , где точки F и L – середины ребер соответственно AP и DP , причем MF ║ BP и EL ║ CP (прямые пересечения двух параллельных плоскостей третьей плоскостью параллельны).

2 . При параллельном переносе на вектор трапеция MELF отобразится на равную ей трапецию BCHK , где K и H – середины ребер соответственно PB и CP . Причем MF ║ BP и

EL ║ CP (прямые пересечения двух параллельных плоскостей третьей плоскостью параллельны).

3. При параллельном переносе на вектор трапеция MELF отобразится на равную ей трапецию BCHK , где K и H – середины ребер соответственно PB и CP . Если при этом

4. С учетом получаем откуда . Это означает, что:

Ответ:

1а. У правильной пирамиды одна из граней может быть прямоугольным

треугольником:

• Да Нет
• Да
• Нет

2а. У правильной пирамиды одна из боковых граней может быть

перпендикулярна основанию пирамиды:

• Да Нет
• Да
• Нет

3а. У правильной пирамиды все боковые грани – равнобедренные

треугольники:

• Да Нет
• Да
• Нет

4а. Боковое ребро правильной пирамиды называется апофемой:

• Да Нет
• Да
• Нет

5а. У правильной пирамиды две боковые грани могут быть

перпендикулярными друг другу:

• Да Нет
• Да
• Нет

6в. Скрещивающиеся ребра правильной треугольной пирамиды

перпендикулярны друг другу:

• Да Нет
• Да
• Нет

7в. Смежные ребра правильной треугольной пирамиды попарно

перпендикулярны друг другу:

• Да Нет
• Да
• Нет

8в. Если все грани пирамиды – правильные треугольники и длина ребра

равна а, то площадь поверхности пирамиды равна

• Да Нет
• Да
• Нет

9с. Из проволоки длиной 68 см можно изготовить каркас правильной

четырехугольной пирамиды с длиной бокового ребра 10 см.

• Да Нет
• Да
• Нет

10с. Сумма внутренних углов развертки правильной шестиугольной

пирамиды равна 18000:

• Да Нет
• Да
• Нет

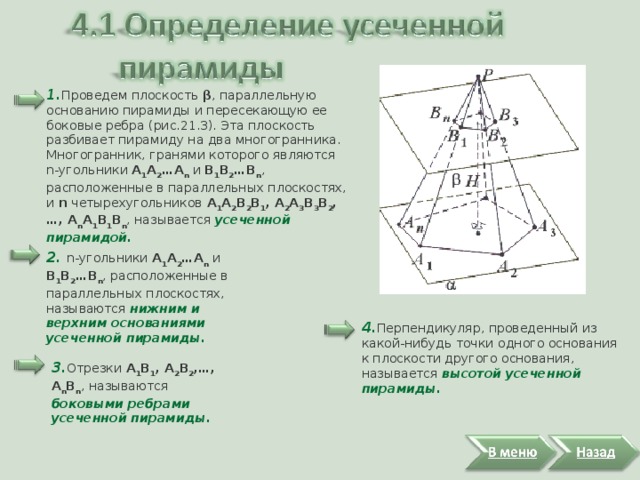
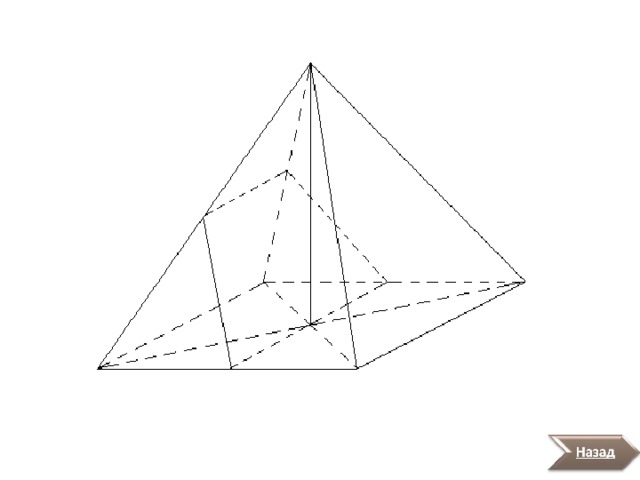
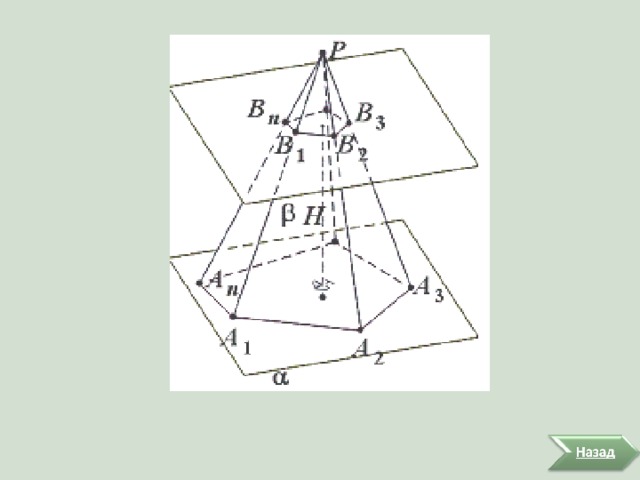
1. Проведем плоскость β , параллельную основанию пирамиды и пересекающую ее боковые ребра (рис.21.3). Эта плоскость разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n-угольники А 1 А 2 … А n и В 1 В 2 … В n , расположенные в параллельных плоскостях, и n четырехугольников А 1 А 2 В 2 В 1 , А 2 А 3 В 3 В 2 , … , А n А 1 В 1 В n , называется усеченной пирамидой.

2. n-угольники А 1 А 2 … А n и В 1 В 2 … В n , расположенные в параллельных плоскостях, называются нижним и верхним основаниями усеченной пирамиды.

4. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усеченной пирамиды.

3. Отрезки А 1 В 1 , А 2 В 2 , … , А n В n , называются боковыми ребрами усеченной пирамиды.

Четырехугольники А 1 А 2 В 2 В 1 , А 2 А 3 В 3 В 2 , … , А n А 1 В 1 В n , называются боковыми гранями усеченной пирамиды.

Теорема

Боковые грани усеченной пирамиды - трапеции.

Доказательство

1. Рассмотрим боковую грань А 1 А 2 В 2 В 1 .

2. Стороны А 1 А 2 и В 2 В 1 параллельны друг другу, поскольку принадлежат параллельным прямым, по которым плоскость А 1 РА 2 пересекается с плоскостями α и β (свойство 1 параллельных плоскостей урок 5).

3. Стороны А 1 В 1 , и А 2 В 2 непараллельны друг другу, поскольку их продолжения пересекаются в точке Р. Следовательно, четырехугольник А 1 А 2 В 2 В 1 - трапеция (по определению).

4. Аналогично можно доказать, что и остальные боковые грани - трапеции.

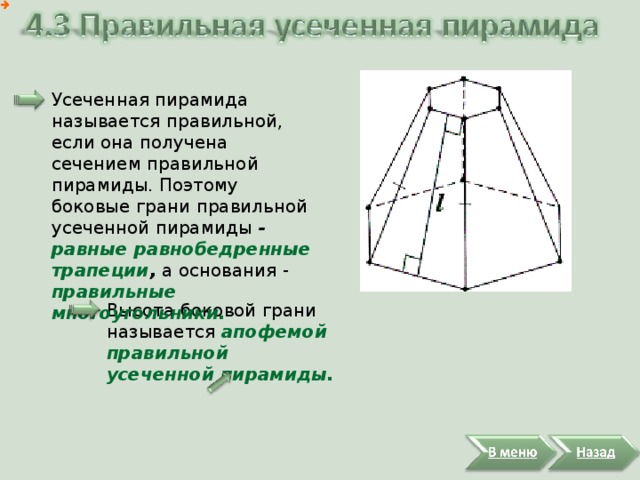
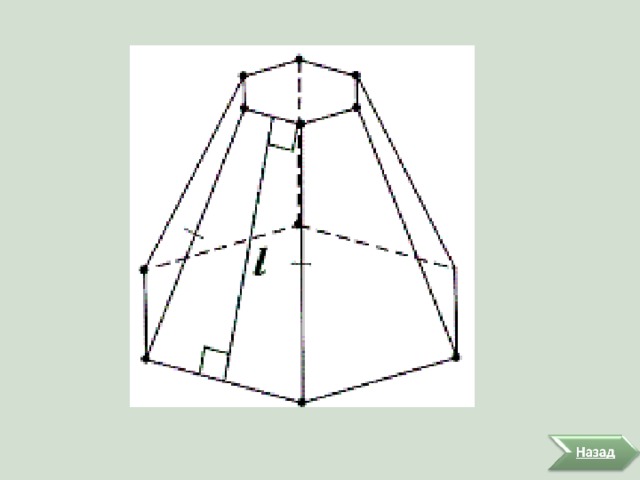
Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды. Поэтому боковые грани правильной усеченной пирамиды - равные равнобедренные трапеции , а основания - правильные многоугольники.

Высота боковой грани называется апофемой правильной усеченной пирамиды.

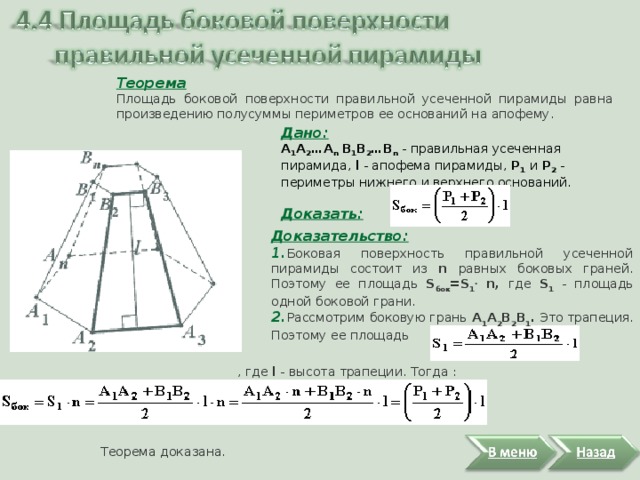
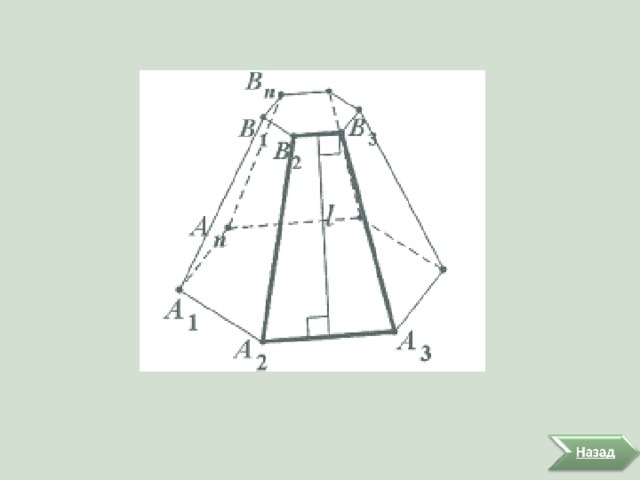
Теорема

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований на апофему.

Дано:

А 1 А 2 …А n В 1 В 2 …В n - правильная усеченная пирамида, l - апофема пирамиды, Р 1 и Р 2 - периметры нижнего и верхнего оснований.

Доказать:

Доказательство:

1. Боковая поверхность правильной усеченной пирамиды состоит из n равных боковых граней. Поэтому ее площадь S бок =S 1 . n, где S 1 - площадь одной боковой грани.

2. Рассмотрим боковую грань А 1 А 2 В 2 В 1 . Это трапеция. Поэтому ее площадь

, где l - высота трапеции. Тогда :

Теорема доказана.

1а. У четырехугольной усеченной пирамиды сумма числа граней и ребер равна:

• Восемнадцати Шестнадцати Четырнадцати Двенадцати
• Восемнадцати
• Шестнадцати
• Четырнадцати
• Двенадцати

2а. У пятиугольной усеченной пирамиды разность числа ребер и вершин равна:

• Трем Четырем Нулю Пяти
• Трем
• Четырем
• Нулю
• Пяти

3а. У шестиугольной усеченной пирамиды произведение числа вершин на число граней равно:

• Семидесяти двум Шестидесяти Девяноста шести Сорока двум
• Семидесяти двум
• Шестидесяти
• Девяноста шести
• Сорока двум

4a. При сечении усеченной пирамиды плоскостью, проходящей через основания, сечение представляет собой:

• только треугольники только трапеции треугольники и четырехугольники треугольники и пятиугольники
• только треугольники
• только трапеции
• треугольники и четырехугольники
• треугольники и пятиугольники

5a. Боковые грани усеченной пирамиды:

• треугольники и трапеции треугольники и четырехугольники только треугольники только трапеции
• треугольники и трапеции
• треугольники и четырехугольники
• только треугольники
• только трапеции

6a. Апофемой правильной усеченной пирамиды называется:

• высота боковой грани высота пирамиды расстояние между ее основаниями длина бокового ребра
• высота боковой грани
• высота пирамиды
• расстояние между ее основаниями
• длина бокового ребра

7б. Сечение четырехугольной усеченной пирамиды плоскостью, проходящей через середины трех боковых ребер – это:

• треугольник, параллельный основанию четырехугольник, параллельный основанию треугольник, непараллельный основанию четырехугольник, непараллельный основанию
• треугольник, параллельный основанию
• четырехугольник, параллельный основанию
• треугольник, непараллельный основанию
• четырехугольник, непараллельный основанию

8б. У четырехугольной усеченной пирамиды прямоугольной трапецией может быть:

• только одна грань от одной до 4-х и 6 граней от одной до 6 граней от двух до 4-х граней
• только одна грань
• от одной до 4-х и 6 граней
• от одной до 6 граней
• от двух до 4-х граней

9c. Сумма всех внутренних углов развертки треугольной усеченной пирамиды равна:

• 1440 0 1620 0 1260 0 1800 0
• 1440 0
• 1620 0
• 1260 0
• 1800 0

10c. Число диагоналей n-угольной усеченной пирамиды равно:

• 2n(n-3) n(n-2) n(n-3) n(n-3)/2
• 2n(n-3)
• n(n-2)
• n(n-3)
• n(n-3)/2

ПИРАМИДЫ В ГИЗЕ (Великая пирамида Хуфу в центре).

РАЗВАЛИНЫ ГОРОДА ТЕОТИУАКАН в межгорной долине примерно в 50 км к северо-востоку от города Мехико. Археологами вскрыты две громадные пирамиды Солнца и Луны, множество небольших пирамид и других построек.

ПИРАМИДА египетского фараона Униса.

Начиная с 1990 года, на территории России и других стран ближнего и дальнего зарубежья проводятся работы по строительству и изучению Пирамид высотой 11, 22 и 44 метра. Только в 2000-2002 годах Пирамиды построены в Ницце (Франция), Астрахани, Петрозаводске, Екатеринбурге, Сочи, Алуште, Ростове.

Бутик-отель в виде пирамиды в Дубаях.

Разбор задач:

• Задача №1 ( Пирамида)
• Задача №2 (Частные виды пирамид)
• Задача №3 (Правильная пирамида)

Тесты:

• Тест по пирамиде
• Тест по частным видам пирамид
• Тест по правильной пирамиде
• Тест по усеченной пирамиде

Подготовка к ЕГЭ:

Тесты

№ 1 Три боковых ребра треугольной пирамиды попарно перпендикулярны и равны 16 см, 12 см и 12 см. Найдите площадь полной поверхности пирамиды.

№ 2 В основании пирамиды прямоугольник, диагональ которого равна а. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы 30 0 и 45 0 . Найдите площадь полной поверхности пирамиды.

№ 3 Основание пирамиды – прямоугольный треугольник с гипотенузой с . Каждое боковое ребро образует с плоскостью основания угол  . Найдите высоту пирамиды.

№ 4 Боковая грань правильной четырехугольной пирамиды наклонена к плоскости основания под углом 60 0 . Апофема равна 4 см. Найдите площадь всей поверхности пирамиды.

40 см 2

80 см 2

48 см 2

36 см 2

№ 5 В правильной треугольной пирамиде сторона основания равна а , а высота 2а . Под каким углом наклонены боковые грани к плоскости основания?

arctg2 √3

60 0

arctg4 √3

30 0

№ 6 В правильной треугольной пирамиде боковые грани наклонены к основанию под углом 60 0 . Расстояние от вершины основания до боковой грани равно 3 √3. Найдите площадь боковой поверхности пирамиды.

20

20 √3

24 √3

12 √3

№ 7 Высота правильной четырехугольной усеченной пирамиды равна 7 см, стороны оснований равны 2 см и 10 см. Найдите боковое ребро пирамиды.

9см

12 см

10 см

7 √3 см

№ 8 В правильной четырехугольной усеченной пирамиде площадь диагонального сечения равна 4 √ 6 см 2 , а стороны оснований равны 5 см и 3 см. Найдите площадь всей поверхности пирамиды.

96 см 2

64см 2

66 см 2

32 см 2

№ 9 В правильной треугольной усеченной пирамиде боковые грани наклонены к плоскости основания под углом 30 0 , а стороны оснований равны 6 см и 3 см. Найдите площадь боковой поверхности пирамиды.

18 √3 см 2

27 см 2

36 см 2

12 см 2

№ 10 Дан тетраэдр АВСD.  BАD=  САD=  CBA=60 0 , AВ=АC=6 см, DА=10cм. Найдите стороны треугольника DСВ.

2

3

4

1

№ 11 Дан тетраэдр АВСD. Постройте его сечение плоскостью, проходящей через точки K,М и N , если K,М и N лежат соответственно на серединах ребер AD, ВD и ВC. Найдите площадь сечения, если все ребра тетраэдра равны а.

1

2

3

4