Презентация к уроку геометрии на тему "Пирамида"

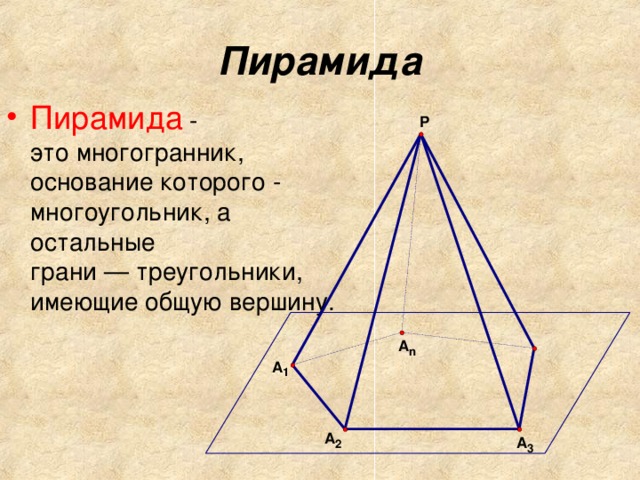
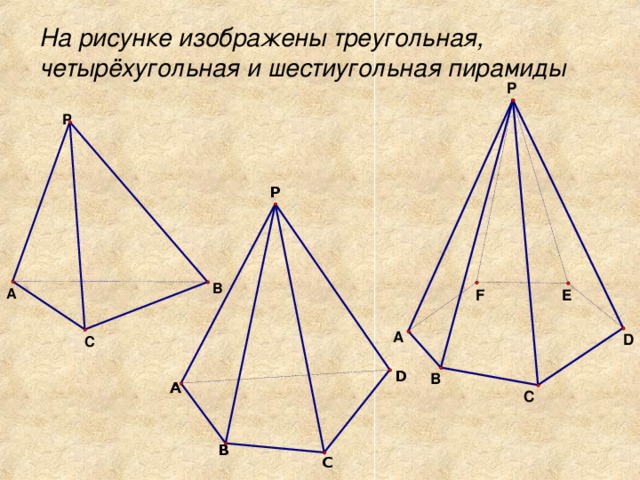
Пусть Q - плоский многоугольник в плоскости a и S - точка, не принадлежащая плоскости а. Соединим каждую точку М многоугольника Q с точкой S отрезком МS. Отрезки МS заполняют некоторый многогранник. Этот многогранник называется пирамидой.

Пирамида называется n-угольной, если Q - n-угольник.

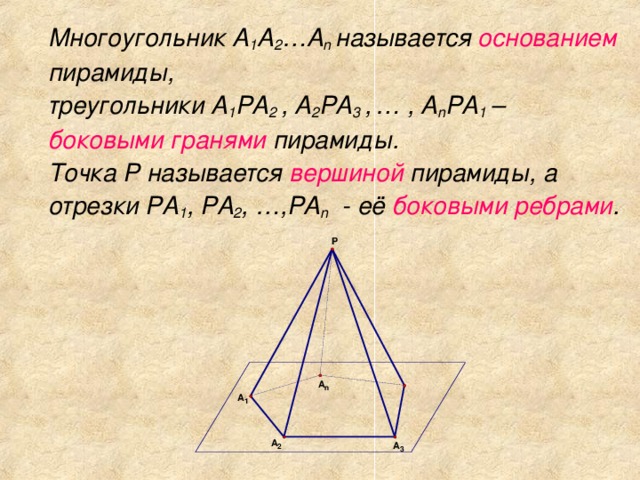
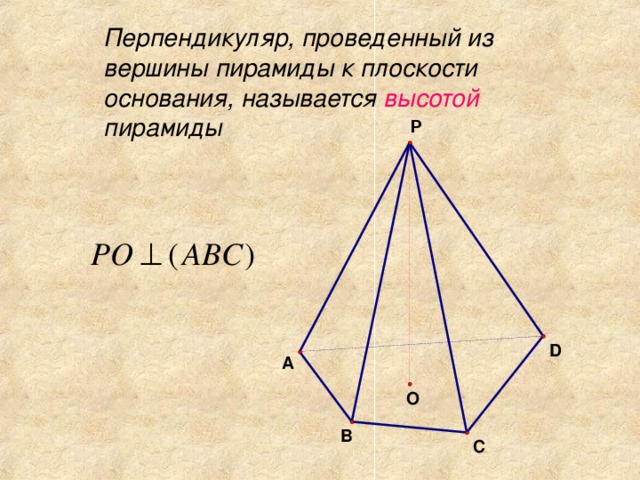
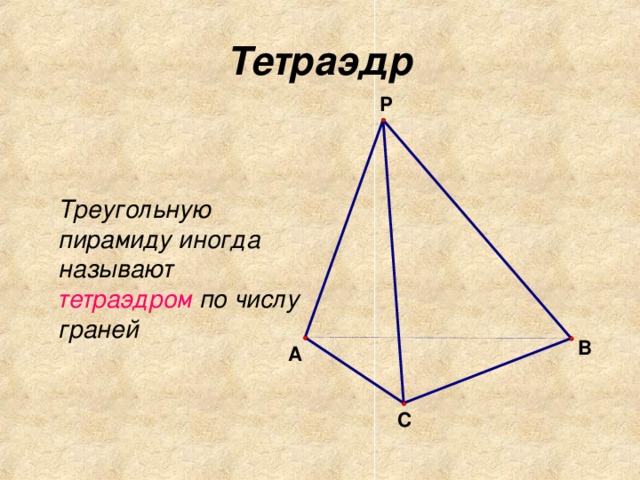
Треугольная пирамида называется также тетраэдром. Многоугольник Q называется основанием пирамиды, а точка S - вершиной пирамиды. Высотой пирамиды называется отрезок перпендикуляра, проведенного через вершину к плоскости ее основания; концами этого отрезка являются вершина пирамиды и основание перпендикуляра; на рисунке 1 SH - высота пирамиды.

(Высотой пирамиды называют длину этого отрезка.) Пусть A, B, C, …, K - вершины многоугольника Q, лежащего в основании пирамиды. Тогда треугольники ASB, BCS, …, KSA называются боковыми гранями пирамиды, а отрезки AS, BS, CS, …, KS боковыми ребрами.

Сечение пирамиды, проходящее через вершину и диагональ основания, называется диагональным сечением пирамиды. Например, треугольник ACS - диагональное сечение пирамиды.

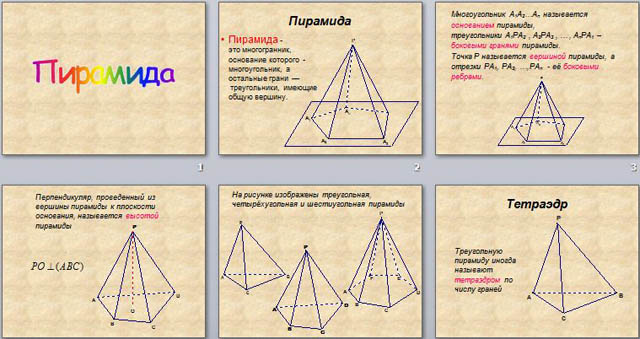
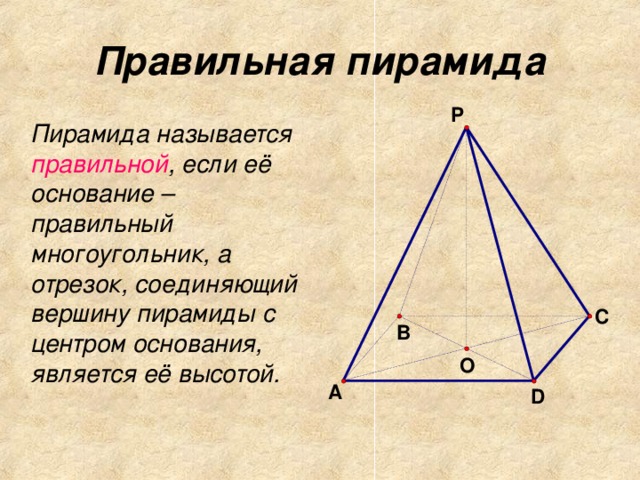
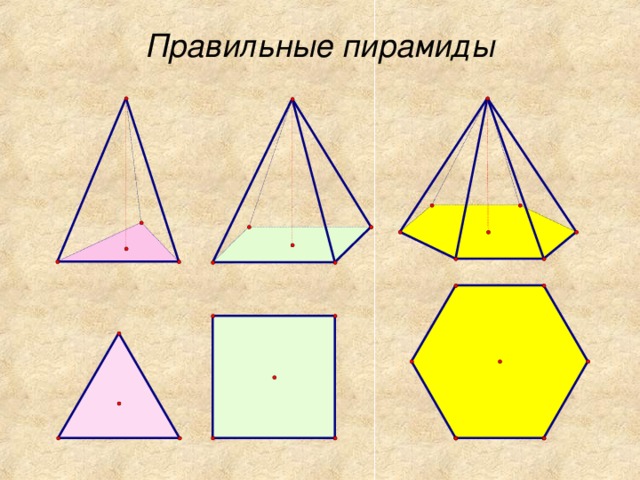
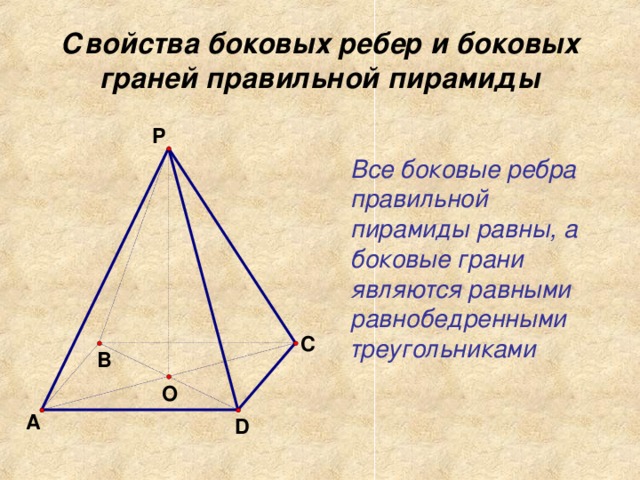
Пирамида называется правильной, если основанием ее является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника (центром основания). Осью правильной пирамиды называется прямая, содержащая ее высоту.

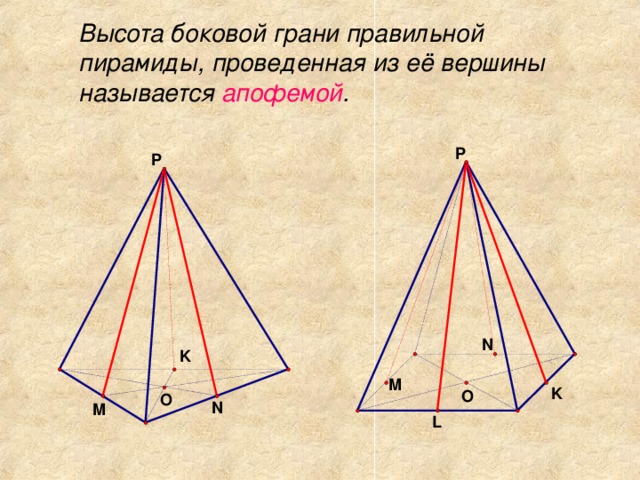
Высота боковой грани правильной пирамиды, проведенная из вершины пирамиды, называется апофемой пирамиды (обозначение hбок). Все апофемы правильной пирамиды равны между собой.

SO - высота, а SD - апофема.

Часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию, называется усеченной пирамидой. Параллельные грани ABC и A1B1C1 называются основаниями, а отрезок перпендикуляра ОО1, опущенного из какой-нибудь точки О1 верхнего основания на нижнее основание, - высотой усеченной пирамиды.

Усеченная пирамида называется правильной, если она составляет часть правильной пирамиды. Ее ось - прямая, проходящая через центры оснований. Боковые грани правильной усеченной пирамиды - равные равнобочные трапеции; их высоты называются апофемами.

Пирамида

• Пирамида - это многогранник, основание которого - многоугольник, а остальные грани — треугольники, имеющие общую вершину.

Многоугольник A 1 A 2 …A n называется основанием пирамиды,

треугольники A 1 PA 2 , A 2 PA 3 , … , A n PA 1 – боковыми гранями пирамиды.

Точка P называется вершиной пирамиды, а отрезки PA 1 , PA 2 , …,PA n - её боковыми ребрами .

Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды

На рисунке изображены треугольная, четырёхугольная и шестиугольная пирамиды

Тетраэдр

Треугольную пирамиду иногда называют тетраэдром по числу граней

Правильная пирамида

Пирамида называется правильной , если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.

Правильные пирамиды

Свойства боковых ребер и боковых граней правильной пирамиды

Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками

Высота боковой грани правильной пирамиды, проведенная из её вершины называется апофемой .

Боковая поверхность пирамиды равна сумме площадей боковых граней пирамиды.

Полная поверхность пирамиды равна сумме боковой поверхности пирамиды и площади основания пирамиды.

S( бок.) = S(SAB) +

+ S(SBC) + S(SCD)+

+S(SDE) + S(SEA)

Объем пирамиды равен произведению одной третьей площади основания пирамиды на ее высоту.

S( полн.) = S( бок.) +

+ S (осн.)

V = 1/3 S( осн.) * H