Цели:
Обучающая:
вывести формулу для вычисления площади параллелограмма и выработать умение применять ее при решении задач;
Развивающая:
развитие навыков на основе наблюдений делать выводы; развитие компьютерной грамотности, навыков использования компьютеров, развитие навыков самостоятельной работы;
Воспитательная:
воспитание интереса к предмету, повышение мотивации учащихся
Ход урока.
Оргмомент (слайд 1. «Добро пожаловать на урок»)
Проверка домашнего задания
№ 7 заранее на доске
№ 3 по ответам сверить решение № 7 с решением на доске и с решением на экране (слайд 2)

Опрос
карточки 2 шт.
Карточка 1.
Найти площадь прямоугольника.
Карточка 2.
Чему равны стороны прямоугольника, если его периметр равен 74 дм, а площадь 3 м2
у доски 1 чел.
Найти площадь прямоугольника
Работа устно.
Актуализация опорных знаний
Повторить основное свойство площадей (слайд 3).
Вспомнить признаки равенства прямоугольных треугольников (слайд 4)
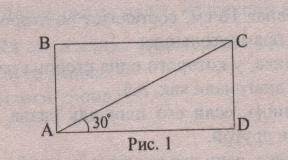
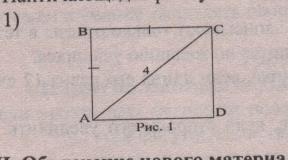
повторить свойство прямоугольного треугольника с углом 300, 450
Решение задач устно
Решить задачи (устно) (слайды 5, 6)
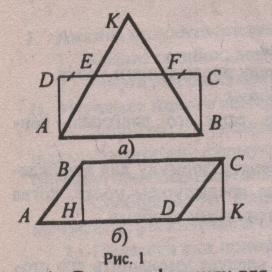
1. АВСД – прямоугольник, ДЕ = СF = ½ ЕF. докажите, что площадь треугольника КЕF в два раза больше площади треугольника ВСF.
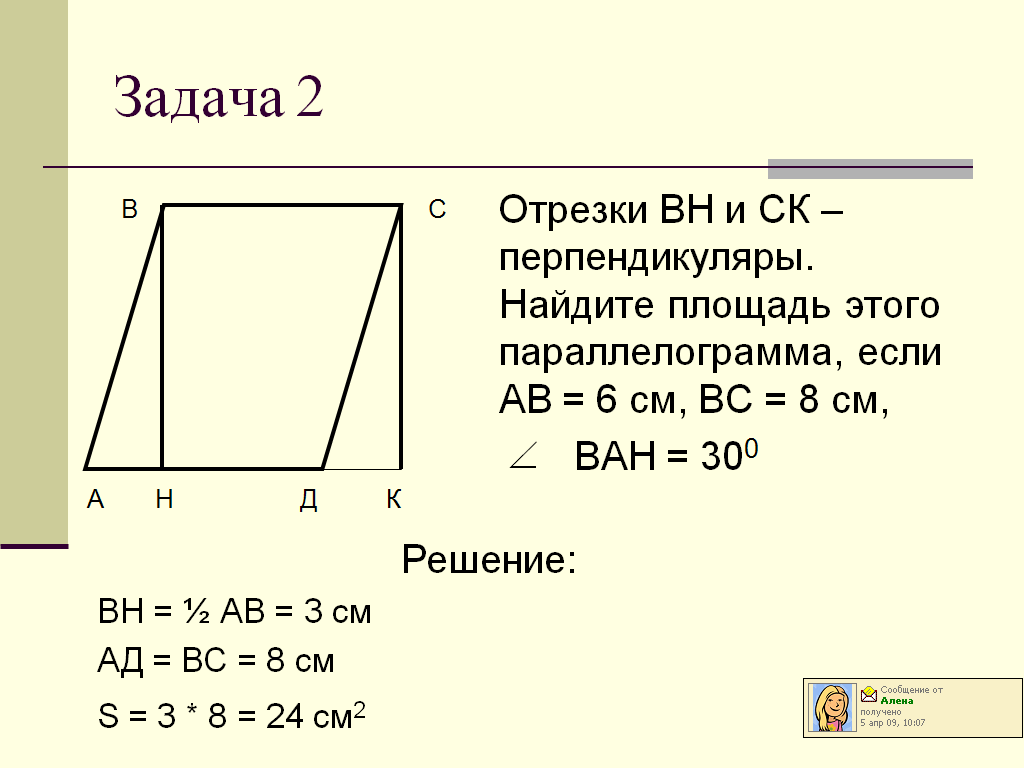
2. Отрезки ВН и СК – перпендикуляры. Найдите площадь этого параллелограмма, если АВ = 6 см, ВС = 8 см, ![]()
Анализ ответа у доски, сбор карточек, выставление оценок.
Изучение нового материала
На сегодняшнем уроке мы продолжим выводить формулы для вычисления площадей фигур. Рассмотрим параллелограмм и выведем формулу площади параллелограмма. Тема урока «Площадь параллелограмма» (слайд 7)
После сегодняшнего урока вы должны будете знать формулу площади параллелограмма, уметь применять ее для решения задач. (слайд 8)
выведем формулу.
А вы поможете мне в этом, отвечая на вопросы, наблюдая и делая выводы (слайд 9)
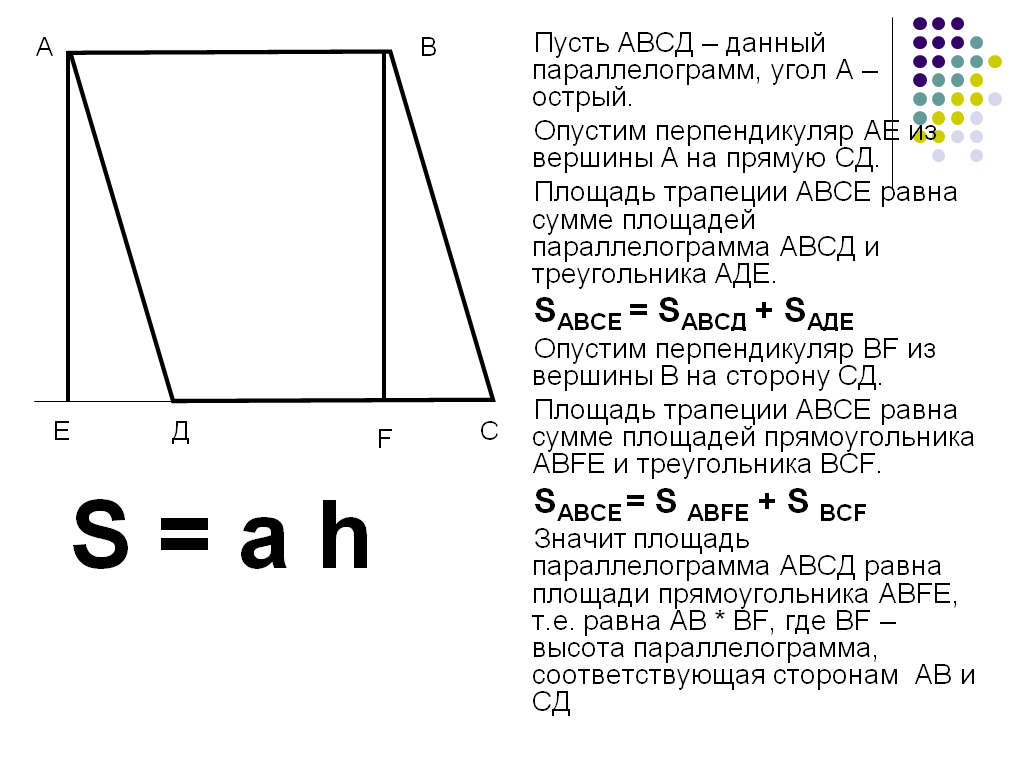
Пусть АВСД – данный параллелограмм, угол А – острый.
Опустим перпендикуляр АЕ из вершины А на прямую СД.
Как называется перпендикуляр в треугольнике, опущенный из вершины на сторону? (высота треугольника) Данный перпендикуляр АЕ мы тоже назовем высотой параллелограмма.
Площадь трапеции АВСЕ равна сумме площадей параллелограмма АВСД и треугольника АДЕ.
SАВСЕ = SABCД + SАДЕ
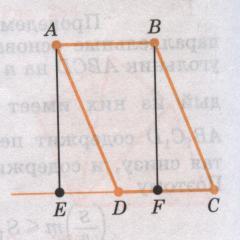
Опустим перпендикуляр ВF из вершины В на сторону СД. А этот перпендикуляр будет являться высотой?
Площадь трапеции АВСЕ равна сумме площадей прямоугольника АВFЕ и треугольника ВСF. SАВСЕ = S АВFЕ + S ВСF
Что можно сказать о треугольниках АДЕ и ВСF? Докажите, что они равны.
Что можно сказать о площадях этих равных треугольников?
Значит площадь параллелограмма АВСД равна площади прямоугольника АВFЕ, т.е. равна АВ * ВF, где ВF – высота параллелограмма, соответствующая сторонам АВ и СД.
Итак, площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
Текущее закрепление.
Решение задач по готовым чертежам
Постройте параллелограмм, произведите необходимые измерения и вычислите его площадь (Какие измерения необходимо произвести?)
Решение письменных задач.
На доске 2 человека одновременно решают задачи.
Найти площадь параллелограмма, если его основание равно 7 см, а высота равна 4 дм.
Найти высоту параллелограмма, площадь которого равна 280 см2, а основание 4 дм. (слайд 10)
Решить задачу у доски, подробно разобрать.
Большая сторона параллелограмма равна 8 см, а меньшая – 4 см; большая высота его равна 10 см. Найти меньшую высоту. (слайд 11)
Как провести большую высоту? меньшую высоту?
№ 11 из учебника на доске.
Проверка знаний учащихся.
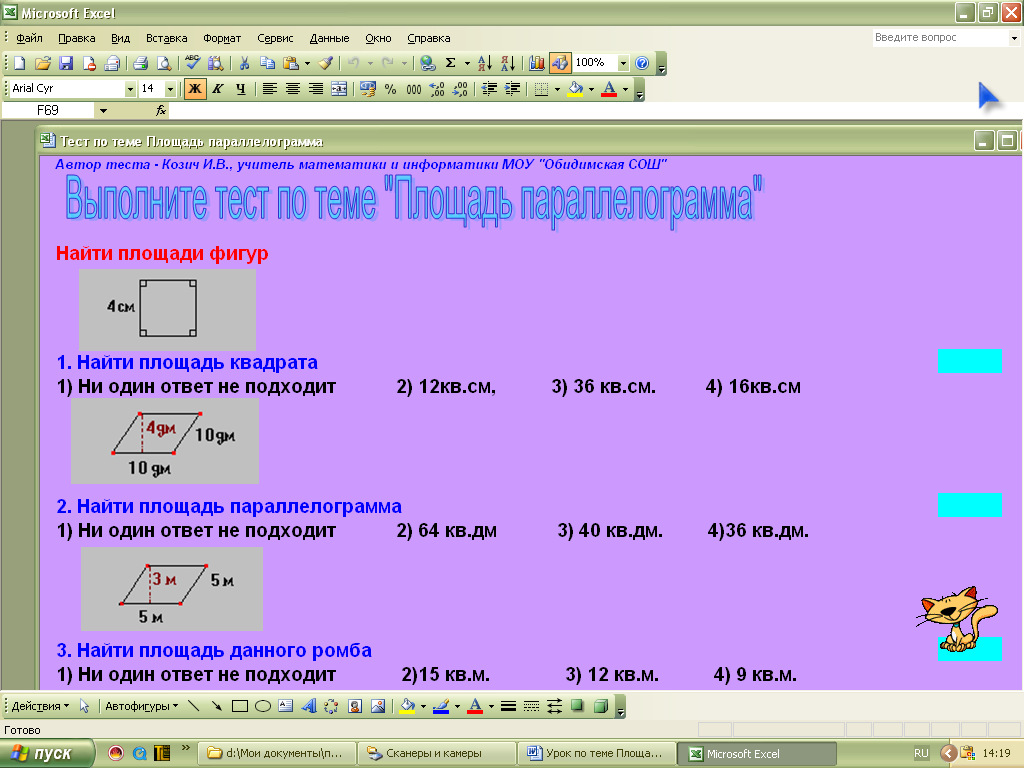
Электронное тестирование
За компьютер садятся все ученики и выполняют электронный тест по теме «Площадь параллелограмма»
Итог урока
Что нового вы узнали на сегодняшнем уроке?
Нравится ли вам электронное тестирование?
На следующем уроке мы узнаем с вами еще другие формулы для вычисления площади параллелограмма.
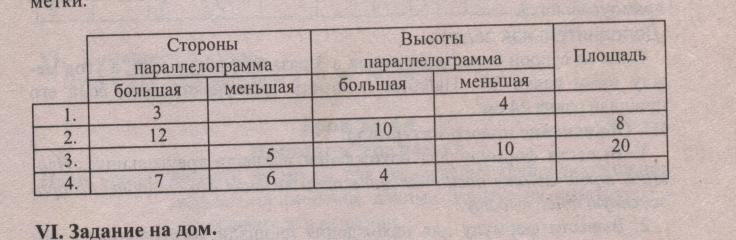
Домашнее задание п.123, № 10, 12, заполнить пустые клетки таблицы.

 Получите свидетельство
Получите свидетельство Вход
Вход








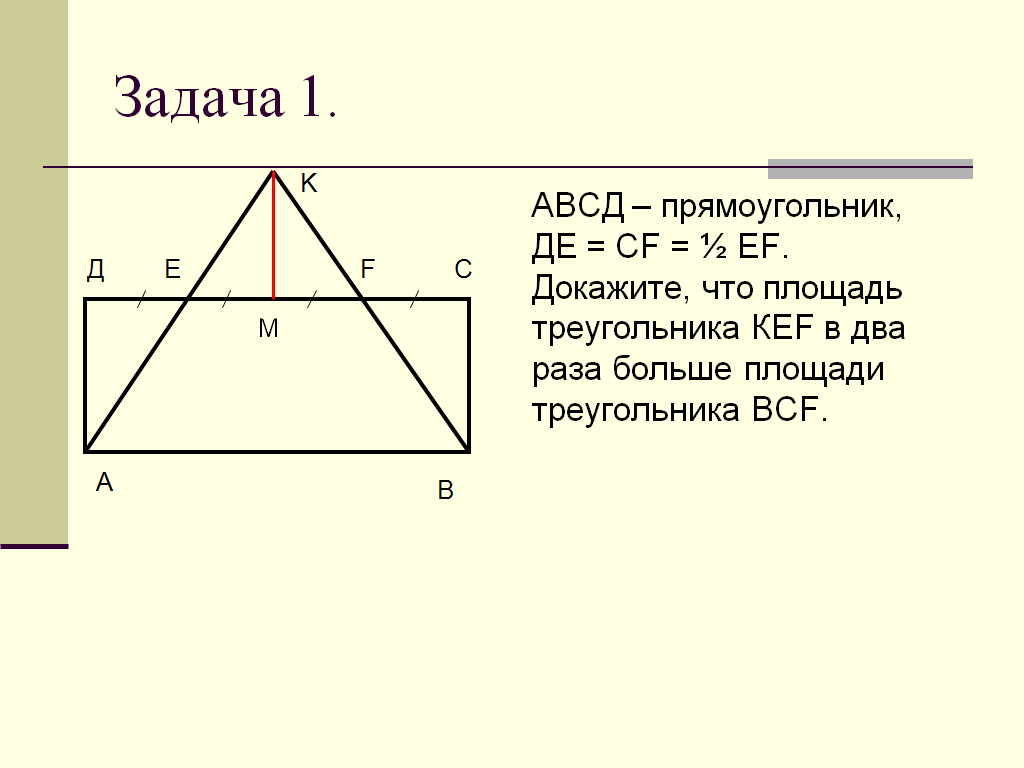
 . АВСД – прямоугольник, ДЕ = СF = ½ ЕF. докажите, что площадь треугольника КЕF в два раза больше площади треугольника ВСF.
. АВСД – прямоугольник, ДЕ = СF = ½ ЕF. докажите, что площадь треугольника КЕF в два раза больше площади треугольника ВСF.

 ак называется перпендикуляр в треугольнике, опущенный из вершины на сторону? (высота треугольника) Данный перпендикуляр АЕ мы тоже назовем высотой параллелограмма.
ак называется перпендикуляр в треугольнике, опущенный из вершины на сторону? (высота треугольника) Данный перпендикуляр АЕ мы тоже назовем высотой параллелограмма.











 Площадь параллелограмма (1.07 MB)
Площадь параллелограмма (1.07 MB)
 1
1 1442
1442 48
48 Нравится
0
Нравится
0


