Конспект урока по геометрии "Площадь параллелограмма"

Организационная структура урока

ЭТАП 1

Организационный момент, сообщение темы урока.

Цель

Сообщить учащимся цели и задачи урока, создать благоприятную атмосферу в классе.

Длительность этапа

2 минуты

Функции преподавателя на данном этапе

Организующая.

ЭТАП 2

Актуализация знаний учащихся

Длительность этапа

15 минут

Цель

Активизация логического мышления, подготовка учащихся к восприятию нового материала.

Функции преподавателя на данном этапе

Организующая, направляющая.

Содержание этапа

1.Проверка домашнего задания: к доске вызываются двое учащихся и готовят решение домашней задачи

№ 454 а). и б). , третий учащийся приглашается для доказательства формулы площади прямоугольника.

2.Индивидуальная работа: 4 человека работают по индивидуальным карточкам (приложение 1).

3.Теоретический опрос: пока вызванные учащиеся готовятся, проводится фронтальный опрос по теории

- в каких единицах измеряется площадь?

- назовите специальную единицу для измерения

площадей;

- перечислите основные свойства площадей;

- назовите формулу площади квадрата;

- дайте определение параллелограмма.

По окончании теоретического опроса проводится проверка задачи № 454 (домашняя), заслушивается вывод формулы площади прямоугольника. После ответа учащегося другой ученик, названный учителем, комментирует ответ и выставляет оценку за вывод формулы прямоугольника.

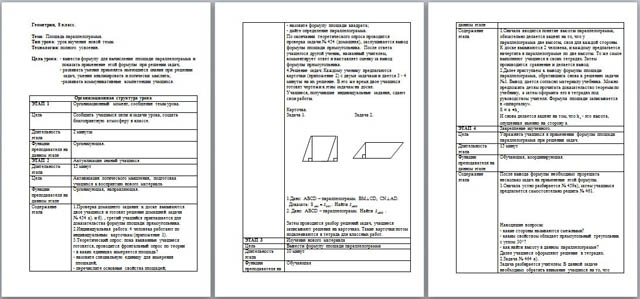
4.Решение задач: Каждому ученику предлагаются карточки (приложение 2) с двумя задачами и дается 3 - 4 минуты на их решение. В это же время двое учащихся готовят чертежи к этим задачам на доске.

Учащиеся, получившие индивидуальные задания, сдают свои работы.

Карточка.

Задача 1. Задача 2.

1.Дано: АВСD – параллелограмм. BMCD, CNAD.

Доказать: S. Найти

2. Дано: АВСD – параллелограмм. Найти .

Затем проводится разбор решений задач, учащиеся записывают решения на карточках. Такие карточки потом подклеиваются в тетрадь для классных работ.

ЭТАП 3

Изучение нового материала

Цель

Вывести формулу площади параллелограмма

Длительность этапа

10 минут

Функции преподавателя на данном этапе

Обучающая

Содержание этапа

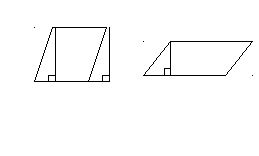
1.Сначала вводится понятие высоты параллелограмма, обязательно делается акцент на то, что у параллелограмма две высоты, своя для каждой стороны.

К доске вызываются 2 человека, и каждому предлагается начертить в параллелограмме по две высоты. То же самое выполняют учащиеся в своих тетрадях. Затем производится сравнение и делается вывод.

2.Далее приступаем к выводу формулы площади параллелограмма, обратившись снова к решению задачи №1. Вывод дается согласно материалу учебника. Можно предложить детям прочитать доказательство теоремы по учебнику, а затем оформить его в тетрадях под руководством учителя. Формула площади записывается

в «шпаргалку».

S = a h

И снова делается акцент на том, что h- это высота, опущенная именно на сторону a.

ЭТАП 4

Закрепление изученного.

Цель

Упражнять учащихся в применении формулы площади параллелограмма при решении задач.

Длительность этапа

15 минут

Функции преподавателя на данном этапе

Обучающая, координирующая.

Содержание этапа

После вывода формулы необходимо прорешать несколько задач на применение этой формулы.

1.Сначала устно разбирается № 459а), затем учащимся предлагается самостоятельно решить № 461.

Наводящие вопросы:

- какие стороны называются смежными?

- каким свойством обладает прямоугольный треугольник с углом 30?

- как найти высоту в данном параллелограмме?

Далее учащиеся оформляют решение в тетрадях.

2.Задача № 464 а).

Задача разбирается учителем. В данной задаче необходимо обратить внимание учащихся на то, что высота, проведенная к меньшей стороне, будет большей, и что площадь можно находить через любую из высот, связывая её с соответствующим основанием.

Далее учащимся предлагается решить задачу № 464 б). самостоятельно (с последующей проверкой).

ЭТАП 5

Подведение итогов урока, рефлексия, домашнее задание.

Длительность этапа

3 минуты

Цель

Подвести итоги работы на уроке, обсудить домашнее задание.

Функции преподавателя на данном этапе

Обобщающая

Содержание этапа

1.Подведение итогов урока.

На каждой парте имеется карточка №2, на которой предлагается две совсем простых одношаговых задачи на использование формулы площади параллелограмма и одна более сложная. Учащимся предлагается устно решить те задачи, которые они смогут решить.

Ответы озвучиваются.

Далее обсуждается вопрос о том, что нового узнали на уроке и где это можно применить.

Объявляются оценки.

2. Домашнее задание: Вывод формулы площади параллелограмма, задачи №№ 459 (б, в), 462, 463.

Для задач 462 и 463 еще раз напомнить, каким свойством обладает прямоугольный треугольник с углом 30.

3. Учитель благодарит детей за активную работу на уроке и желает удачного дня.

№1. Периметр квадрата равен 20 см. Прямоугольник имеет такую же площадь, что и квадрат, а одна из его сторон равна 10см. Найдите периметр прямоугольника.

№2. Периметр квадрата равен 40 см. Прямоугольник имеет такую же площадь, что и квадрат, а одна из его сторон равна 20см. Найдите периметр прямоугольника.

№3. Биссектриса угла А прямоугольника АВСD разбивает сторону ВC на отрезки, равные 4см и 5см. Найдите площадь прямоугольника.

№4. Найдите площадь прямоугольника с периметром 60см и отношением сторон 1:2.

1.Дано: АВСD – параллелограмм.

BMCD, CNAD.

Доказать: S. Найти

Решение: ________________________________
________________________________
________________________________
________________________________
________________________________
________________________________

2. Дано: АВСD – параллелограмм.

Найти .

Решение: ________________________________
________________________________
________________________________
________________________________
________________________________

________________________________

№ 1

№ 2

№ 3