Получите свидетельство
Вход
Первый признак равенства треугольников
Теорема:
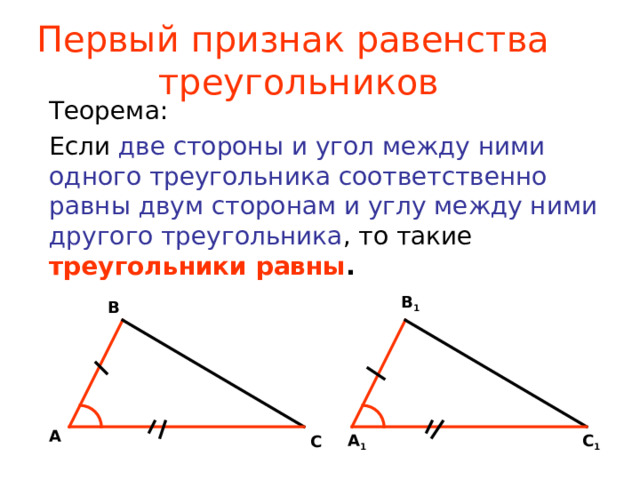
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника , то такие треугольники равны .
В 1
В
А
С 1
А 1
С
ДАНО:
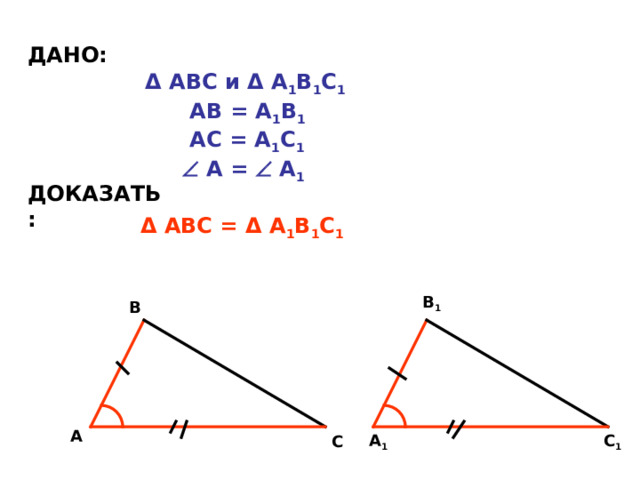
Δ АВС и Δ А 1 В 1 С 1 АВ = А 1 В 1 АС = А 1 С 1 А = А 1
ДОКАЗАТЬ:
Δ АВС = Δ А 1 В 1 С 1
В 1
В
А
С 1
А 1
С
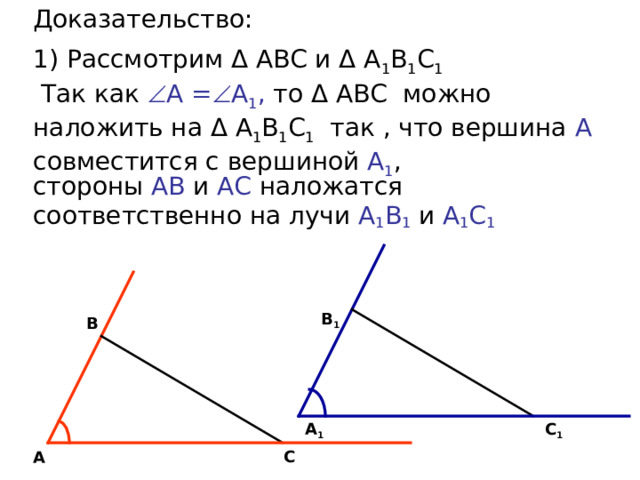
Доказательство: 1) Рассмотрим Δ АВС и Δ А 1 В 1 С 1 Так как А = А 1 , то Δ АВС можно наложить на Δ А 1 В 1 С 1 так , что вершина А совместится с вершиной А 1 ,
стороны АВ и АС наложатся соответственно на лучи А 1 В 1 и А 1 С 1
В 1
В
С 1
А 1
С
А
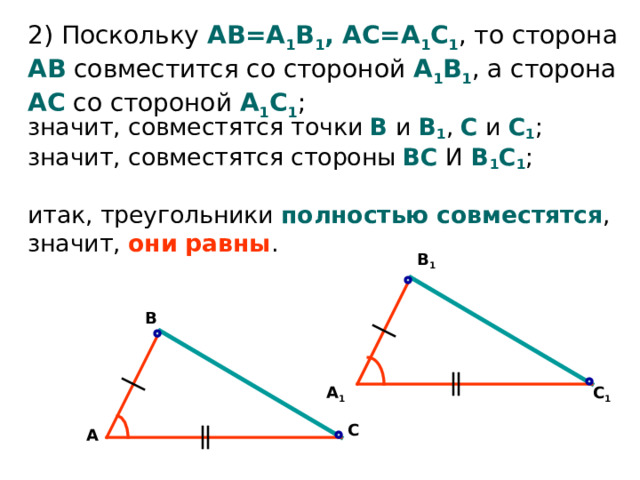
2 ) Поскольку АВ=А 1 В 1 , АС=А 1 С 1 , то сторона АВ совместится со стороной А 1 В 1 , а сторона АС со стороной А 1 С 1 ;
значит, совместятся точки В и В 1 , С и С 1 ; значит, совместятся стороны ВС И В 1 С 1 ; итак, треугольники полностью совместятся , значит, они равны .
В 1
В
С 1
А 1
С
А
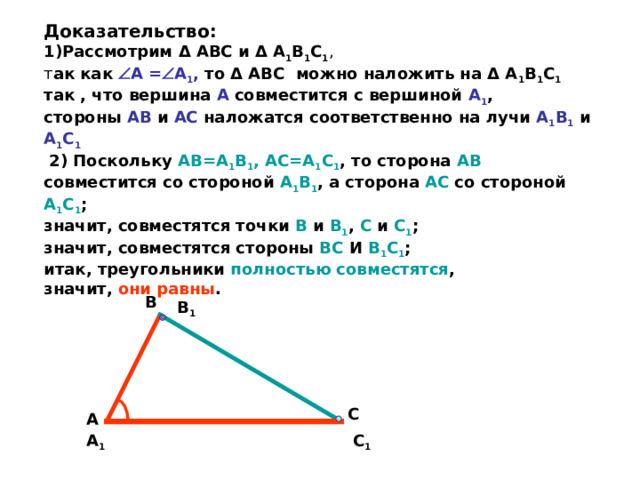
Доказательство: 1)Рассмотрим Δ АВС и Δ А 1 В 1 С 1 , т ак как А = А 1 , то Δ АВС можно наложить на Δ А 1 В 1 С 1 так , что вершина А совместится с вершиной А 1 , стороны АВ и АС наложатся соответственно на лучи А 1 В 1 и А 1 С 1 2) Поскольку АВ=А 1 В 1 , АС=А 1 С 1 , то сторона АВ совместится со стороной А 1 В 1 , а сторона АС со стороной А 1 С 1 ; значит, совместятся точки В и В 1 , С и С 1 ; значит, совместятся стороны ВС И В 1 С 1 ; итак, треугольники полностью совместятся , значит, они равны .
В
В 1
С
А
С 1
А 1
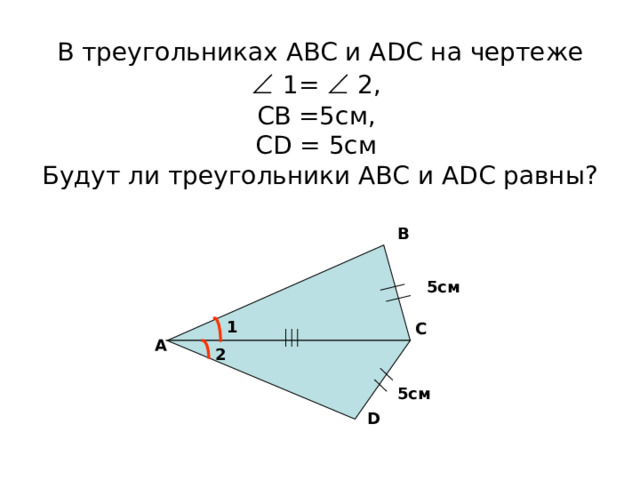
В треугольниках АВС и А D С на чертеже 1= 2, СВ =5см, С D = 5см Будут ли треугольники АВС и А D С равны?
В
5см
1
С
А
2
5см
D
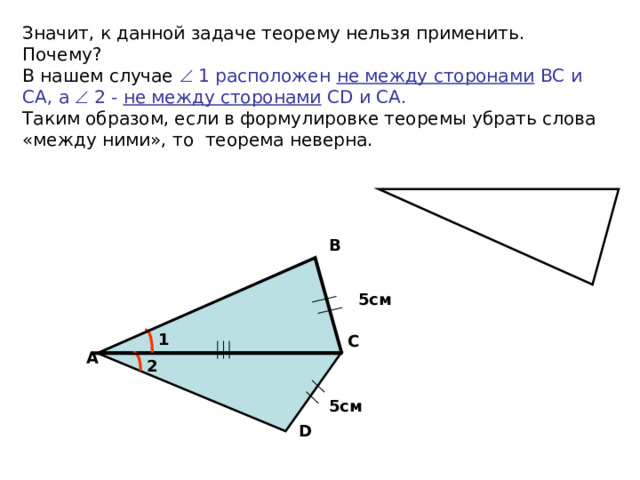
Значит, к данной задаче теорему нельзя применить. Почему? В нашем случае 1 расположен не между сторонами ВС и СА, а 2 - не между сторонами С D и СА. Таким образом, если в формулировке теоремы убрать слова «между ними», то теорема неверна.
В
5см
1
С
А
2
5см
D
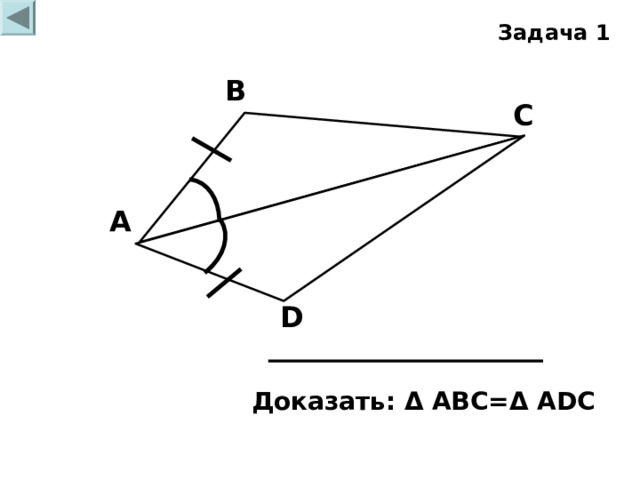
Задача 1
В
С
А
D
Доказать: Δ АВС= Δ А D С
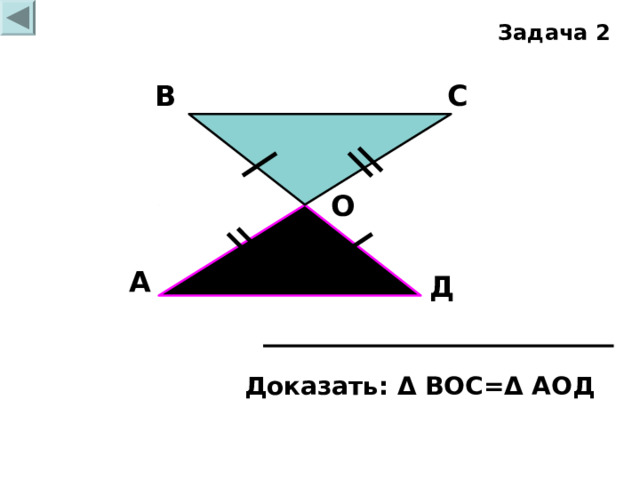
Задача 2
В
С
О
А
Д
Доказать: Δ ВОС= Δ АОД
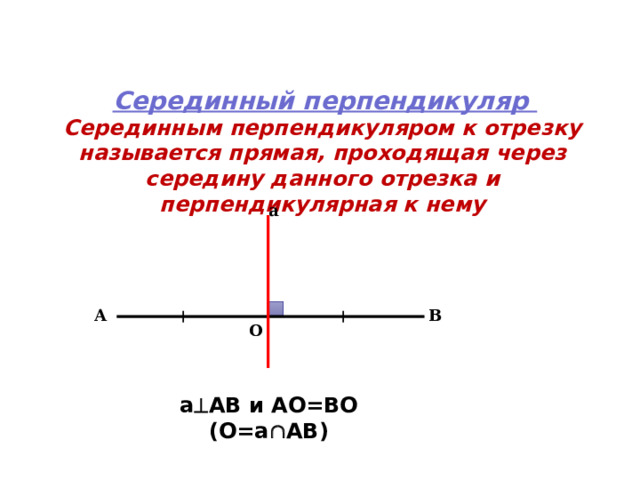
Серединный перпендикуляр
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему
a
A
B
O
а АВ и АО=ВО (О=а АВ)
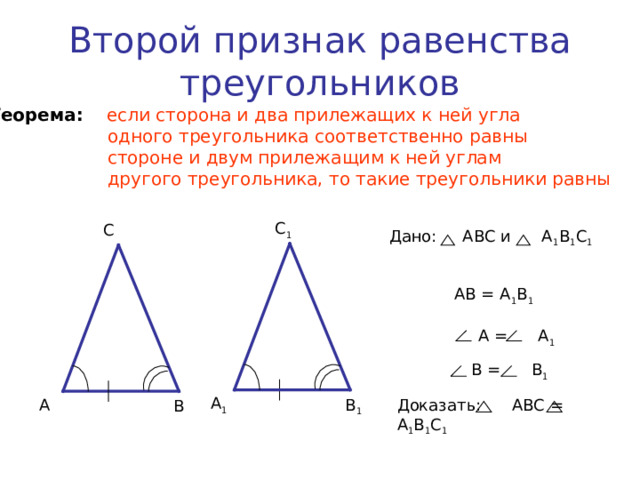
Второй признак равенства треугольников
Теорема: если сторона и два прилежащих к ней угла
одного треугольника соответственно равны
стороне и двум прилежащим к ней углам
другого треугольника, то такие треугольники равны
С 1
С
Дано: АВС и А 1 В 1 С 1
AB = A 1 B 1
A = A 1
B = B 1
А 1
В 1
А
Доказать: АВС = А 1 В 1 С 1
В
Доказательство ( методом наложения) :
Наложим АВС на А 1 В 1 С 1
так, чтобы
луч АВ совместился с лучом А 1 В 1
С 1
С
Значит, вершины А и А 1 совместятся.
Т. к. АВ = А 1 В 1 по условию, то
стороны АВ и А 1 В 1 совместятся.
Значит, вершины В и В 1 совместятся.
A
А 1
В
В 1
Т. к. А = А 1 по условию и лучи АВ, А 1 В 1 совмещены, то и лучи АС, А 1 С 1 совместятся.
Т. к. B = B 1 по условию и вершины В и В 1 совмещены, то и
лучи ВА, В 1 А 1 совместятся, также совместятся лучи ВС и В 1 С 1 .
Значит, точки пересечения С и С 1 совмещённых лучей также совместятся
Значит, стороны треугольников совместятся и, следовательно,
треугольники при наложении совпадают, значит, они равны.
Первый и второй признак равенства треугольников. (311 KB)
0
676
24
Нравится
0
