Первообразная и интеграл

Первообразная и интеграл

Автор: Кулиш Л.Н.

учитель математики

Пик знаний

«Исследуй всё, пусть для тебя на первом месте будет разум» Пифагор

Проверим «рюкзаки»

Ответ:

Проверка домашнего задания : Найдите площадь фигуры ограниченной линиями: y=-0,5x 2 +2x, y=-0,5x+2

Решение:

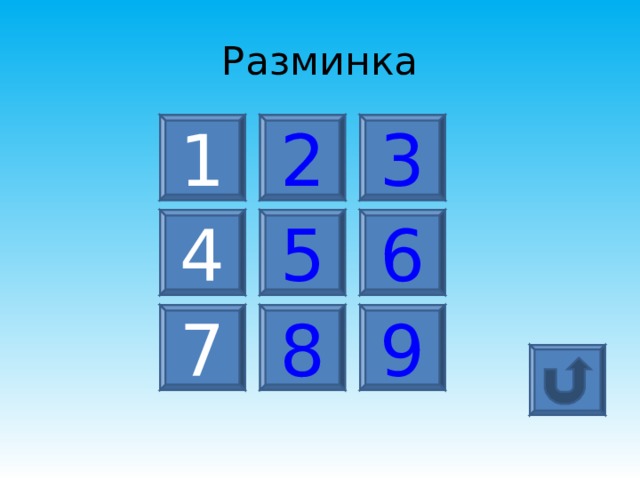
Разминка

2

3

1

4

5

6

8

9

7

• Какие из функций

у=2 , у=4 ,у=2х+3, у= -1 являются первообразными для функции у= ?

(1балл)

2. Сформулируйте основное свойство первообразной.

(1балл)

3. Сформулируйте три правила нахождения первообразных. (2балла)

4. Какую фигуру называют криволинейной трапецией?

(1балл)

5. В чем заключается геометрический смысл интеграла? (1балл)

6. В чем заключается физический смысл определенного интеграла? (1балл)

7. В чем заключается геометрический смысл основного свойства первообразной?

(1балл)

8. Выберите верное равенств о

а)

б)

в)

г)

Как называется эта формула?

(2 балла)

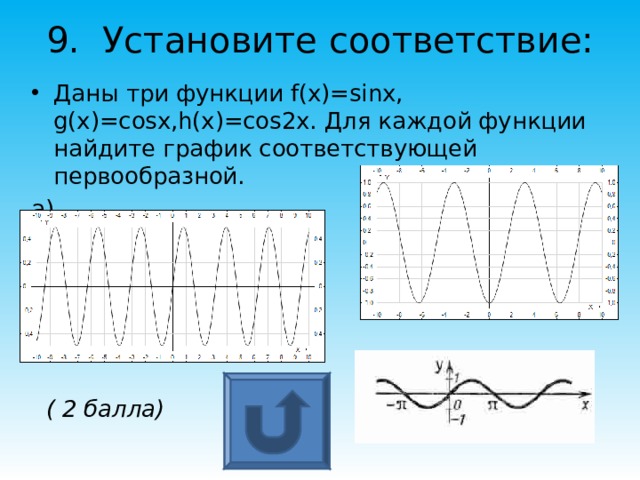
9. Установите соответствие:

• Даны три функции f(x)=sinx, g(x)=cosx,h(x)=cos2x. Для каждой функции найдите график соответствующей первообразной.

а) б)

( 2 балла) в)

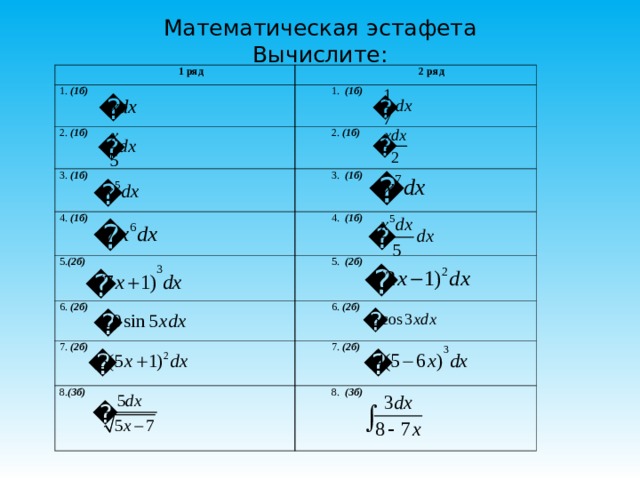
Математическая эстафета Вычислите:

1 ряд

2 ряд

1. (1б )

1. (1б)

2. (1б )

2. (1б)

3. (1б )

3. (1б)

4. (1б )

4. (1б)

5. (2б)

5. (2б)

6. (2б)

6. (2б)

7. (2б)

7. (2б)

8 . (3б)

8. (3б)

Ответы на математическую эстафету:

1 ряд

2 ряд

1.

1.

2.

2.

3.

3.

4.

4.

5.

5.

6.

6.

7.

7.

8 .

8 .

Привал

«Счастливая случайность выпадает лишь на долю хорошо подготовленных умов»

Луи Пастер

Из истории интегрального исчисления

История понятия интеграла уходит корнями к математикам Древней Греции и Древнего Рима. Известны работы учёного Древней Греции - Евдокса Книдского (ок.408—ок.355 до н.э.) на нахождение объёмов тел и вычисления площадей плоских фигур.

Большое распространение интегральное исчисление получило в XVII веке. Учёные: Г. Лейбниц (1646-1716) и И.Ньютон (1643-1727) открыли независимо друг от друга и практически одновременно формулу, названную в последствии формулой Ньютона - Лейбница, которой мы пользуемся. То, что математическую формулу вывели философ и физик никого не удивляет, ведь математика—язык, на котором говорит сама природа.

Символ интеграла был введён

Лейбницем (1675г.)

Этот знак является изменением

формы латинской буквы S .

Из истории интегрального исчисления

Слово «интеграл» было введено Я. Бернулли

(1690). Пределы интегрирования указал уже

Л.Эйлер (1707-1783). В 1697 году появилось

название новой ветви математики

• интегральное исчисление. Его ввёл Бернулли.

Я. Бернулл и

  Если первообразную найти нельзя, то используют

приближенные методы вычисления

определенного интеграла. К приближенным методам

Л.Эйлер вычисления определенного интеграла относятся метод прямоугольников, метод трапеций,

метод Симпсона, метод Монте-Карло.

Самое трудное восхождение

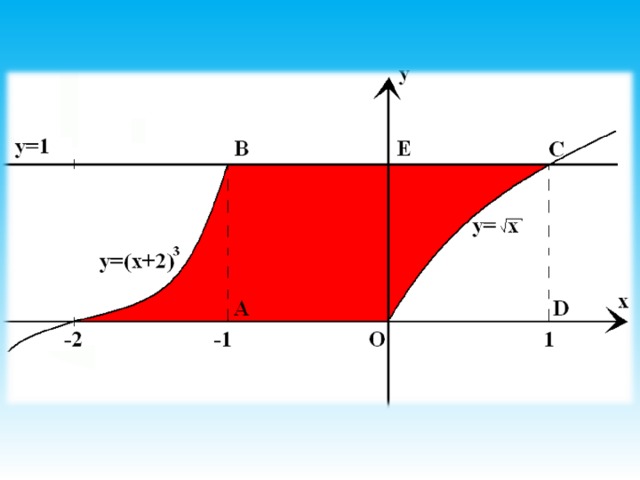
Сколькими способами можно найти площадь фигуры, ограниченной линиями

у= ,

у=(х+2) 3 ,

у=0, у=1.

Последний подъем

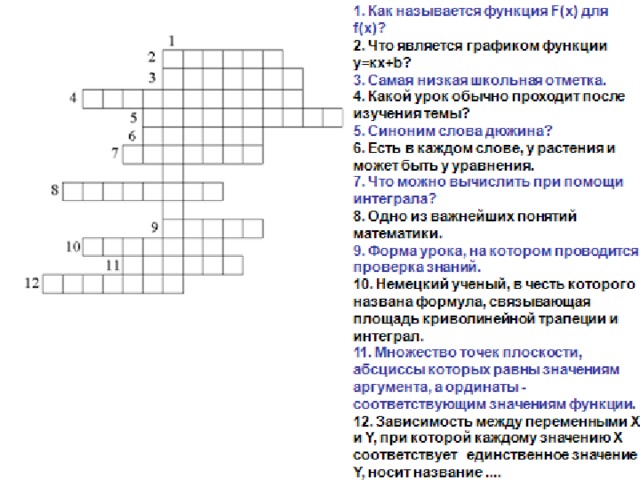
Кроссворд

«Мышление начинается с удивления»,

заметил 2 500 лет назад Аристотель.

Наш соотечественник Сухомлинский считал, что «чувство удивления – могучий источник желания знать; от удивления к знаниям – один шаг».

А математика замечательный предмет для

удивления.

Интегральное исчисление применяется при:

• решении задач из области физики;
• решении экономических задач (на оптимизацию работы фирмы в условиях конкуренции, расчет доходности потребительского кредита);
• решении социально - демографических задач (математическая модель народонаселения Земли и др.).

1. Придумать еще один способ нахождения

площади фигуры.

2. Составить и решить 2 задания:

• вычислить F(x) для f(x)
• вычислить интеграл.

Спасибо за урок!

Домашнее задание на выбор