Первый признак равенства треугольников

Математический диктант

Выпишите углы треугольника DEK, прилежащие к стороне EK.

Выпишите углы треугольника MNP, прилежащие к стороне MN.

Назовите угол треугольника DEK, заключенный между сторонами   DE  и DK;

Назовите угол треугольника MNP, заключенный между сторонами РN и РМ.

Между какими сторонами треугольника DEK заключен угол К;

Между какими сторонами треугольника MNP, заключен угол N;

∆ABC = ∆PSK. Выпишите соответственно равные элементы этих треугольников.

Дано: AB = AC = BC, AD = DC.

P∆ABC =  36 см, Р∆ADC = 40 см.

Найдите стороны  ∆ADC.

ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ

Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Далее в презентации даны задачи и упражнения.

ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ

Теорема

Учитель Козина Н.А.

• Выпишите углы треугольника DEK, прилежащие к стороне EK .

E

D

K

• Выпишите углы треугольника MNP, прилежащие к стороне MN .

N

P

M

• Назовите угол треугольника DEK, заключенный между сторонами DE и DK ;

E

D

K

• Назовите угол треугольника MNP, заключенный между сторонами Р N и РМ.

N

P

M

• Между какими сторонами треугольника DEK заключен угол К;

E

D

K

• Между какими сторонами треугольника MNP, заключен угол N;

N

P

M

• ∆ ABC = ∆PSK . Выпишите соответственно равные элементы этих треугольников.

S

B

K

A

C

P

• Дано: AB = AC = BC, AD = DC.
• P ∆ABC = 36 см, Р ∆ADC = 40 см.
• Найдите стороны ∆ADC.

D

B

A

C

ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ

Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Учебник стр.30.

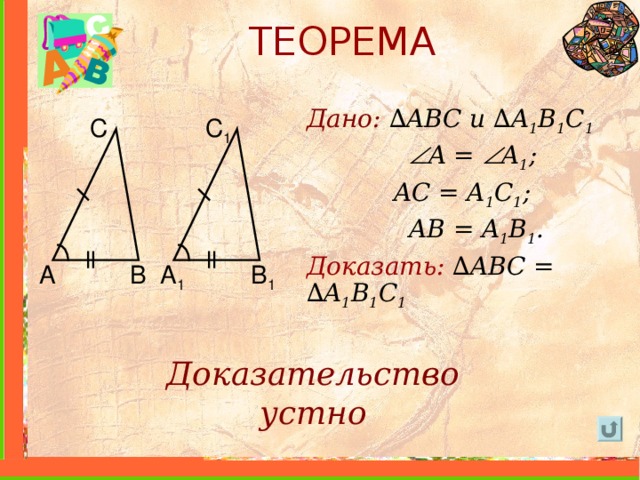
ТЕОРЕМА

Дано: ∆ ABC и ∆ A 1 B 1 C 1

 A =  A 1 ;

AC = A 1 C 1 ;

AB = A 1 B 1 .

Доказать: ∆ ABC = ∆ A 1 B 1 C 1

C 1

С

B 1

A 1

B

A

Доказательство устно

РЕШЕНИЕ ЗАДАЧ

P

K

E

F

T

M

• Что известно о треугольниках MKT и EPF ?
• Какой вывод можно сделать?

РЕШЕНИЕ ЗАДАЧ

D

B

O

A

C

• Что известно о треугольниках ABO и DCO ?
• Чего не хватает для того чтобы сделать вывод о равенстве треугольников?

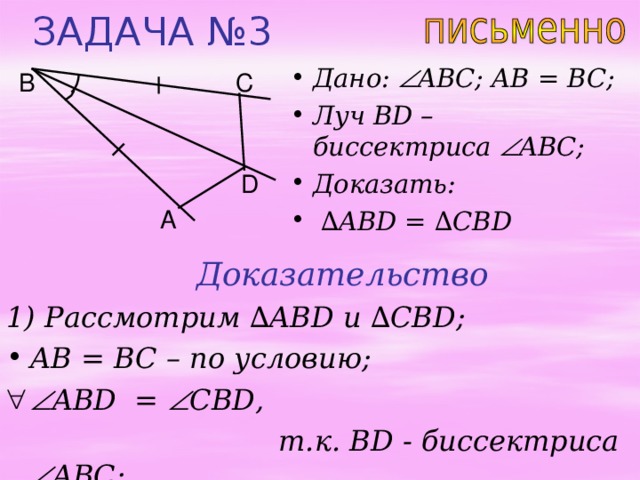
ЗАДАЧА №3

• Дано:  AB С; AB = BC;
• Луч BD – биссектриса  AB С;
• Доказать:
• ∆ ABD = ∆ CBD

C

B

D

A

Доказательство

1) Рассмотрим ∆ ABD и ∆ CBD;

• AB = BC – по условию;

•  ABD =  CBD ,

т.к. BD - биссектриса  AB С;

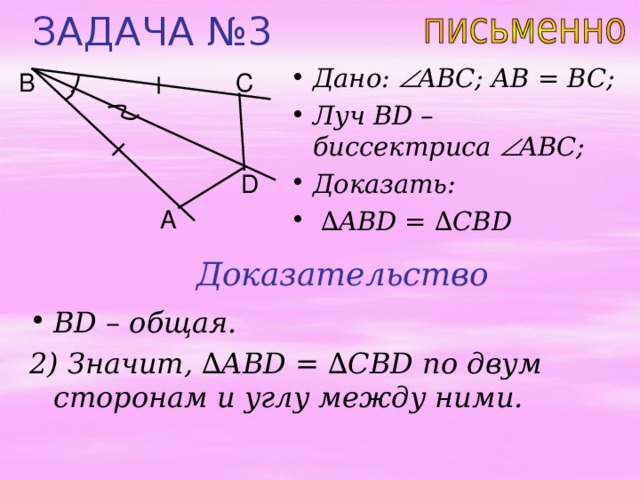
ЗАДАЧА №3

• Дано:  AB С; AB = BC;
• Луч BD – биссектриса  AB С;
• Доказать:
• ∆ ABD = ∆ CBD

C

B

D

A

Доказательство

• BD – общая.

2) Значит, ∆ ABD = ∆ CBD по двум сторонам и углу между ними.

ЗАДАЧА №4

B

C

• Дано: AD = BC;

•  С AD =  B С A ;

• Доказать:
• ∆ ACD = ∆ CAB.

D

A

Доказательство

1) Рассмотрим ∆ ACD и ∆ CAB;

• AD = BC по условию;

•  ACB =  CAD по условию,

• AC – общая.

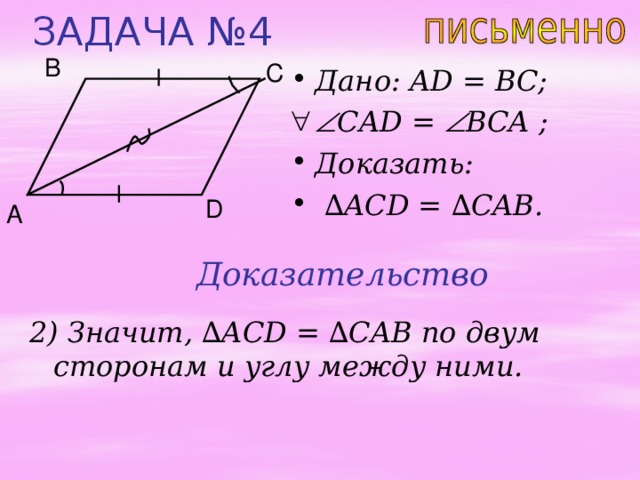
ЗАДАЧА №4

B

C

• Дано: AD = BC;

•  С AD =  B С A ;

• Доказать:
• ∆ ACD = ∆ CAB.

D

A

Доказательство

2) Значит, ∆ ACD = ∆ CAB по двум сторонам и углу между ними.

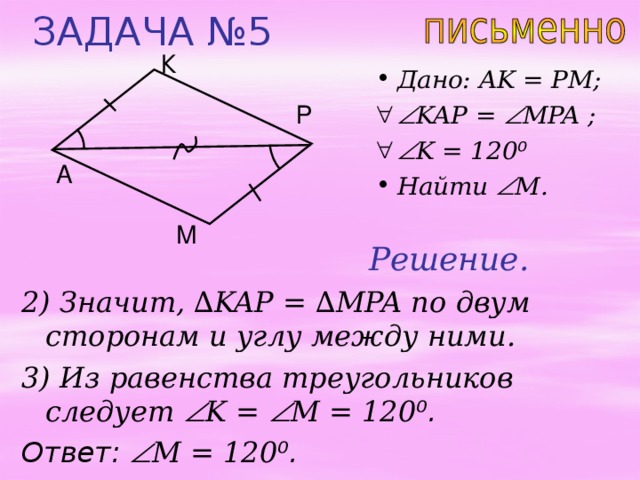
ЗАДАЧА №5

К

• Дано: AK = PM;

•  KAP =  MPA ;
•  K = 120 ⁰

• Найти  M .

Р

A

М

Решение.

1) Рассмотрим ∆ KAP и ∆ MPA;

• AK = MP по условию;

•  KAP =  MPA по условию,

• AP – общая.

ЗАДАЧА №5

К

• Дано: AK = PM;

•  KAP =  MPA ;
•  K = 120 ⁰

• Найти  M .

Р

A

М

Решение.

2) Значит, ∆ KAP = ∆ MPA по двум сторонам и углу между ними.

3) Из равенства треугольников следует  K =  M = 120 ⁰ .

Ответ:  M = 120 ⁰ .

ЗАДАЧА № 6

• Дано: AM = CN;
• AB = BC; MB = 7 см;

•  1 =  2 ;

• Найти NB .
• Доказать MB = NB.

М

N

1

2

C

В

A

Решение.

1) Рассмотрим ∆ AMB и ∆ CNB;

• AM = CN по условию
• AB = BC по условию;

•  1 =  2 по условию,

ЗАДАЧА № 6

• Дано: AM = CN;
• AB = BC; MB = 7 см;

•  1 =  2 ;

• Найти NB .
• Доказать MB = NB.

М

N

1

2

C

В

A

Решение.

1) Рассмотрим ∆ AMB и ∆ CNB;

• AM = CN по условию
• AB = BC по условию;

•  1 =  2 по условию,

ДОМАШНЕЕ ЗАДАНИЕ

П15 вопросы 3,4 Теорему учить формулировку и доказательство по учебнику;

№ 93, 94, 95.

№ 1а

Закончить предложение

∆ ABC = ∆ KPS по первому признаку, если

а) AB = KP, AC = KS и ____=____

б) BC = PS, ∠ B = ∠ P и ___=___

в) ∠ С = ∠ S, ___=___и___=___.

B

C

A

P

S

K

№ 1б

Закончить предложение

∆ ABC = ∆ EFM по первому признаку, если

а) AB = EF , AC = EM и ___=___

б) BC = FM , ∠ B = ∠ F и ___=___

в) ∠ С = ∠ M , ___=___, ___=___.

B

F

M

E

C

A

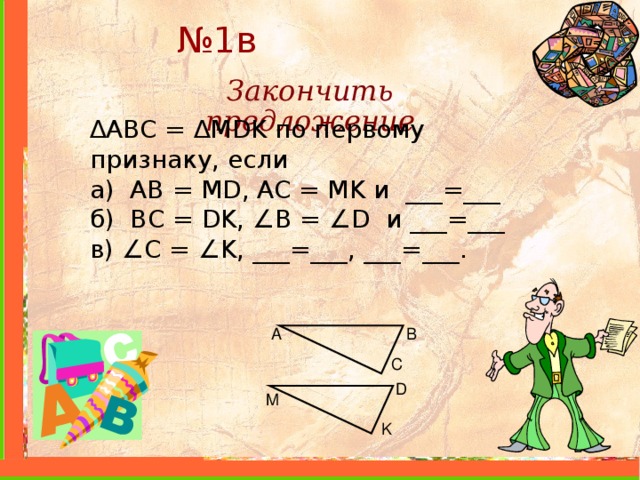
№ 1в

Закончить предложение

∆ ABC = ∆ MDK по первому признаку, если

а) AB = MD , AC = MK и ___=___

б) BC = DK , ∠ B = ∠ D и ___=___

в) ∠ С = ∠ K , ___=___, ___=___.

A

B

C

D

M

K

№ 1г

Закончить предложение

∆ ABC = ∆ NRE по первому признаку, если

а) AB = NR , AC = NE и ___=___

б) BC = RE , ∠ B = ∠ R и ___=___

в) ∠ С = ∠ E , ___=___, ___=___.

N

A

R

B

C

E

• № 1
• Начертите прямую a и отметьте точку М не лежащую на прямой.
• Начертите перпендикуляр MH к прямой а

• № 2
• Начертите треугольник EFK.
• Проведите в нём медиану FM.

• № 3
• Начертите тупоугольный треугольник ABC.
• Проведите в нём высоту BH. (на глаз)

• № 4
• Начертите равнобедренный треугольник KMN с основанием KN.
• Проведите в нём биссектрису ME. (на глаз)

• № 5
• Решете задачу действиями. Без чертежа и краткой записи.
• Периметр равнобедренного треугольника 24см. Основание 10см. Найти боковую сторону.