Тема урока: «Первообразная и интеграл» 11 класс (повторение)
Тип урока: урок оценки и коррекции знаний; повторения, обобщения, формирования знаний, умений, навыков.
Девиз урока: Не стыдно не знать, стыдно не учиться.
Цели урока:
Обучающие: повторить теоретический материал; отработать навыки нахождения первообразных, вычисления интегралов и площадей криволинейных трапеций.
Развивающие: развивать навыки самостоятельного мышления, интеллектуальные навыки (анализ, синтез, сравнение, сопоставление), внимание, память.
Воспитательные: воспитание математической культуры учащихся, повышение интереса к изучаемому материалу, осуществление подготовки к ЕНТ.
План конспект урока.
Организационный момент
Актуализация опорных знаний учащихся.
1.Устная работа с классом на повторение определений и свойств:
1. Что называется криволинейной трапецией?
2. Чему равна первообразная для функции f(х)=х2.
3. В чем заключается признак постоянства функции?
4. Что называется первообразной F(х) для функции f(х) на х I?
I?
5. Чему равна первообразная для функции f(х)=sinx.
6. Верно ли высказывание: «Первообразная суммы функций равна сумме их первообразных»?
7. В чем заключается основное свойство первообразной?
8. Чему равна первообразная для функции f(х)=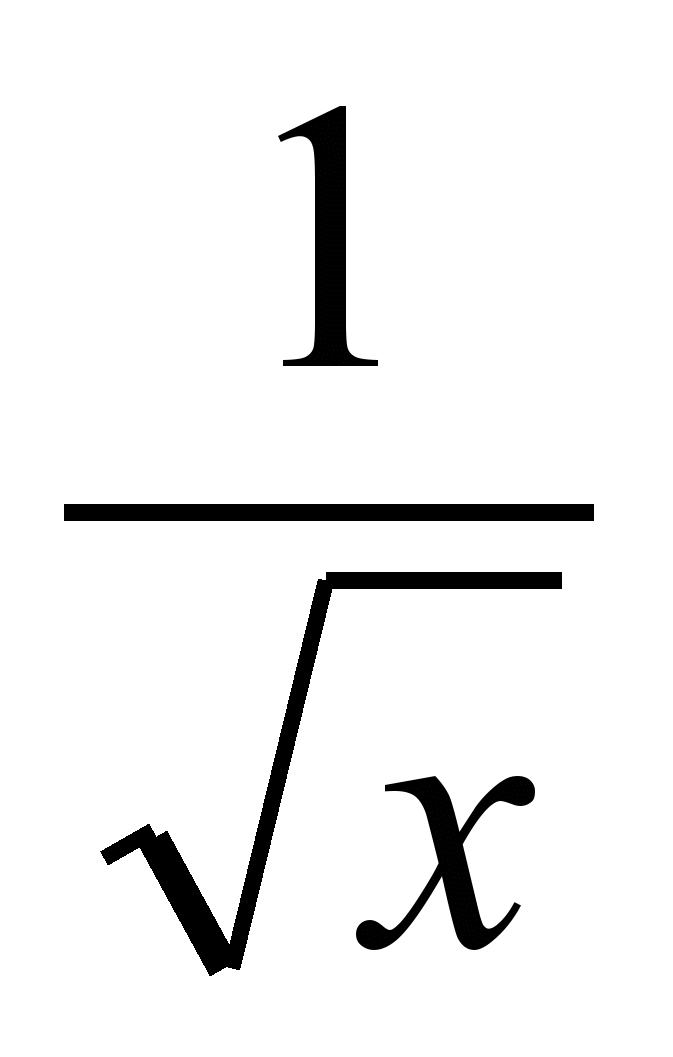 .
.
9. Верно ли высказывание: «Первообразная произведения функций равна произведению их
первообразных»?
10. Что называется неопределенным интегралом?
11.Что называется определенным интегралом?
12.Назовите несколько примеров применения определенного интеграла в геометрии и физике.
Ответы
1. Фигуру, ограниченную графиками функций y=f(x), у=0, х=а, х=b, называют криволинейной трапецией.
2. F(x)=x3/3+С.
3. Если F`(x0)=0 на некотором промежутке, то функция F(x) – постоянная на этом промежутке.
4. Функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для всех х из этого промежутка F`(x)=f(x).
5. F(x)= - cosx+C.
6. Да, верно. Это одно из свойств первообразных.
7. Любая первообразная для функции f на заданном промежутке может быть записана в виде
F(x)+C, где F(x) – одна из первообразных для функции f(x) на заданном промежутке, а С –
произвольная постоянная.
8. F(x)=2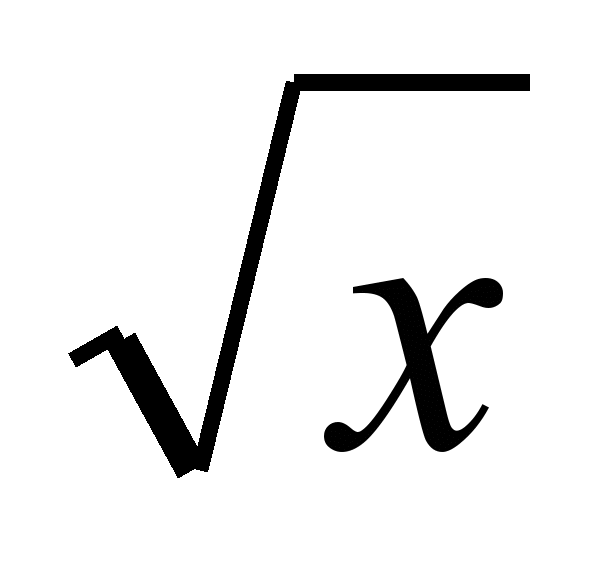 +C.
+C.
9. Нет, не верно. Нет такого свойства первообразных.
10. Если функция у=f(x) имеет на заданном промежутке первообразную у= F(x), то множество всех первообразных у= F(x)+С называют неопределенным интегралом от функции у=f(x).
11. Разность значений первообразной функции в точках b и a для функции у = f (x) на промежутке [a; b] называется определенным интегралом функции f(x) на промежутке [a; b] .
12..Вычисление площади криволинейной трапеции, объемов тел и вычисление скорости тела в определенный промежуток времени.
Применение интеграла. (дополнительно записать в тетрадях)
|
Величины
|
Вычисление производной
|
Вычисление интеграла
|
|
s – перемещение,
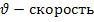 , ,
А – ускорение
|
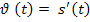
a(t) = 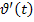
|
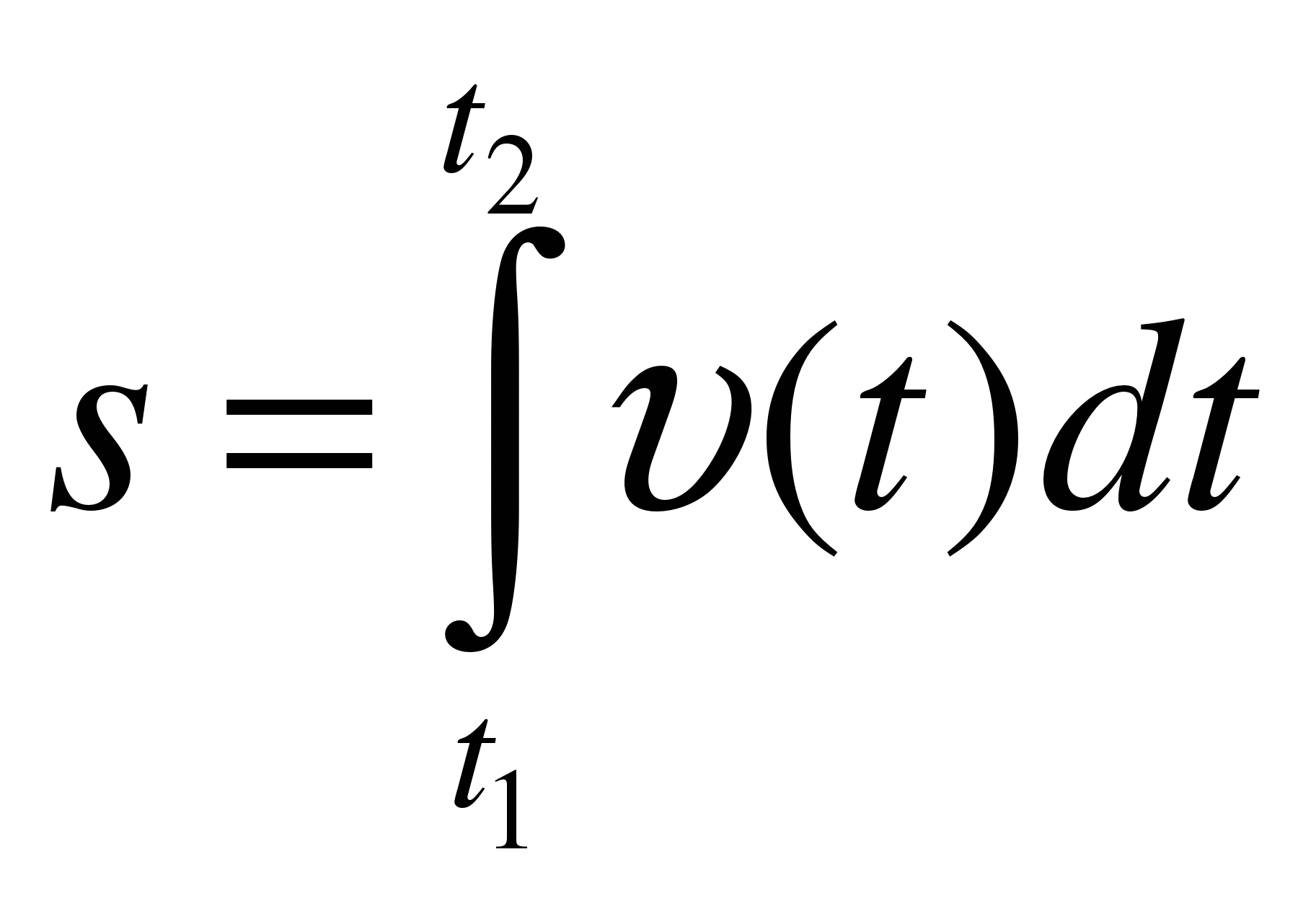
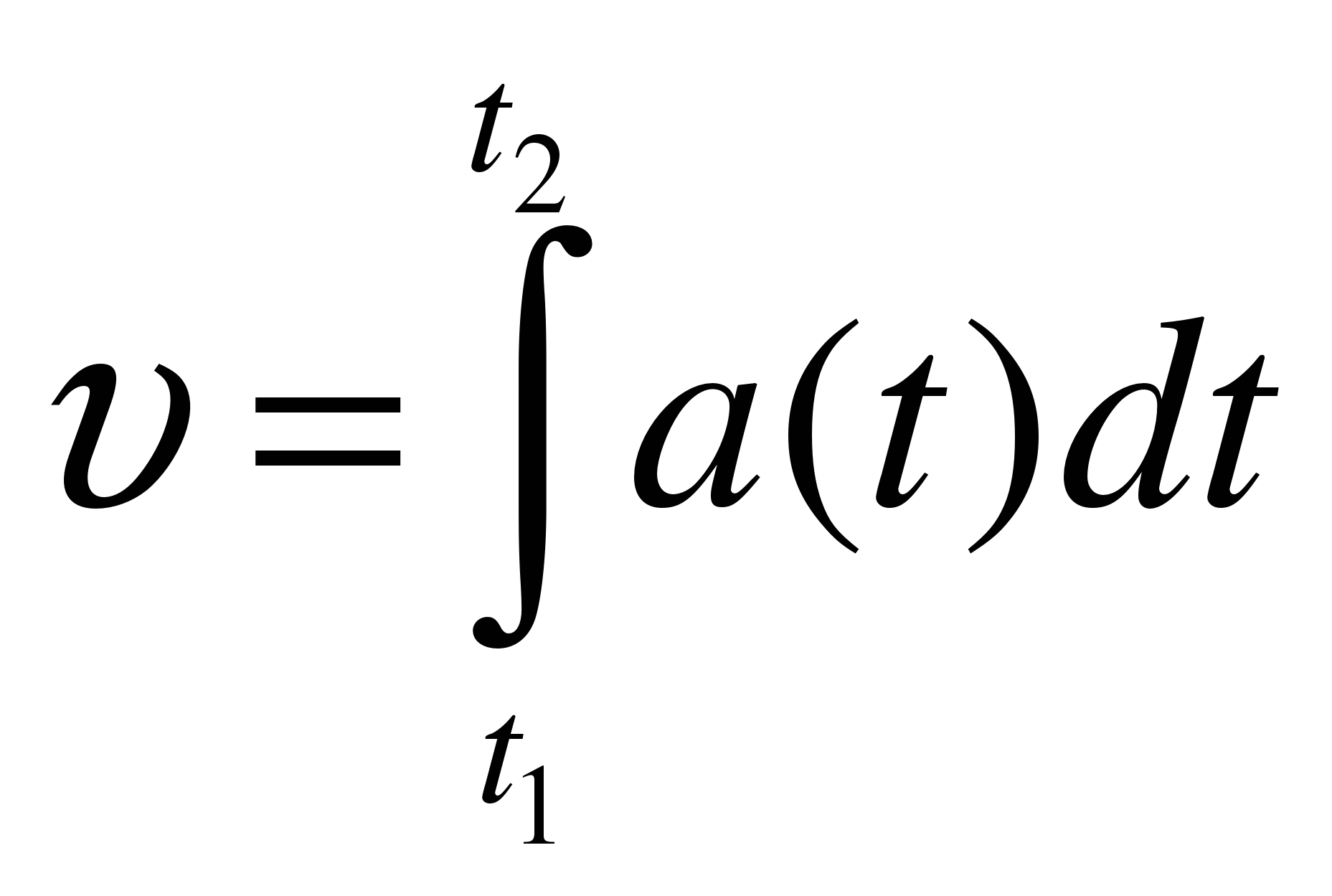
|
|
A - работа,
F – сила,
N - мощность
|
F(x) = A'(x)
N(t) = A'(t)
|
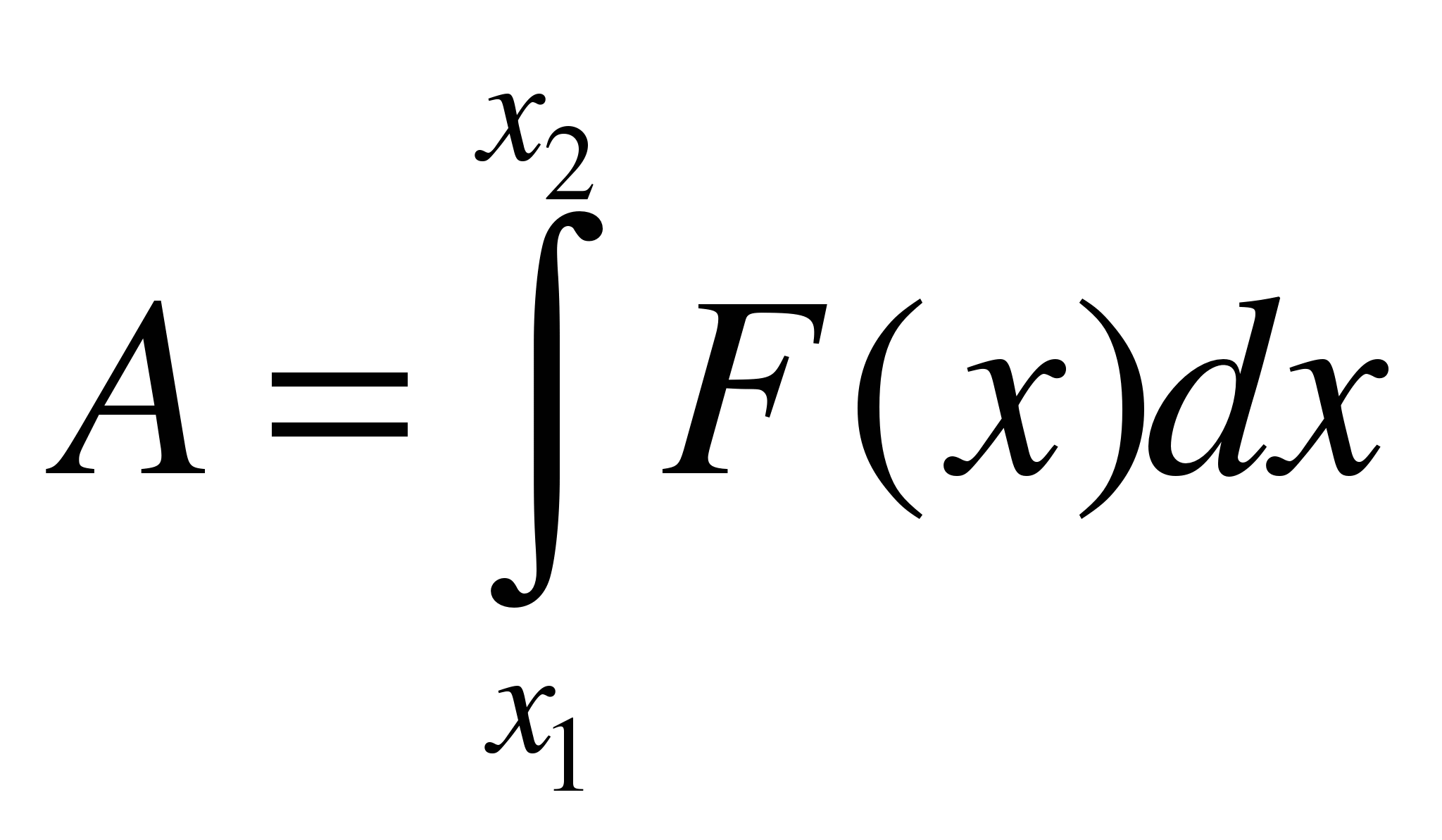
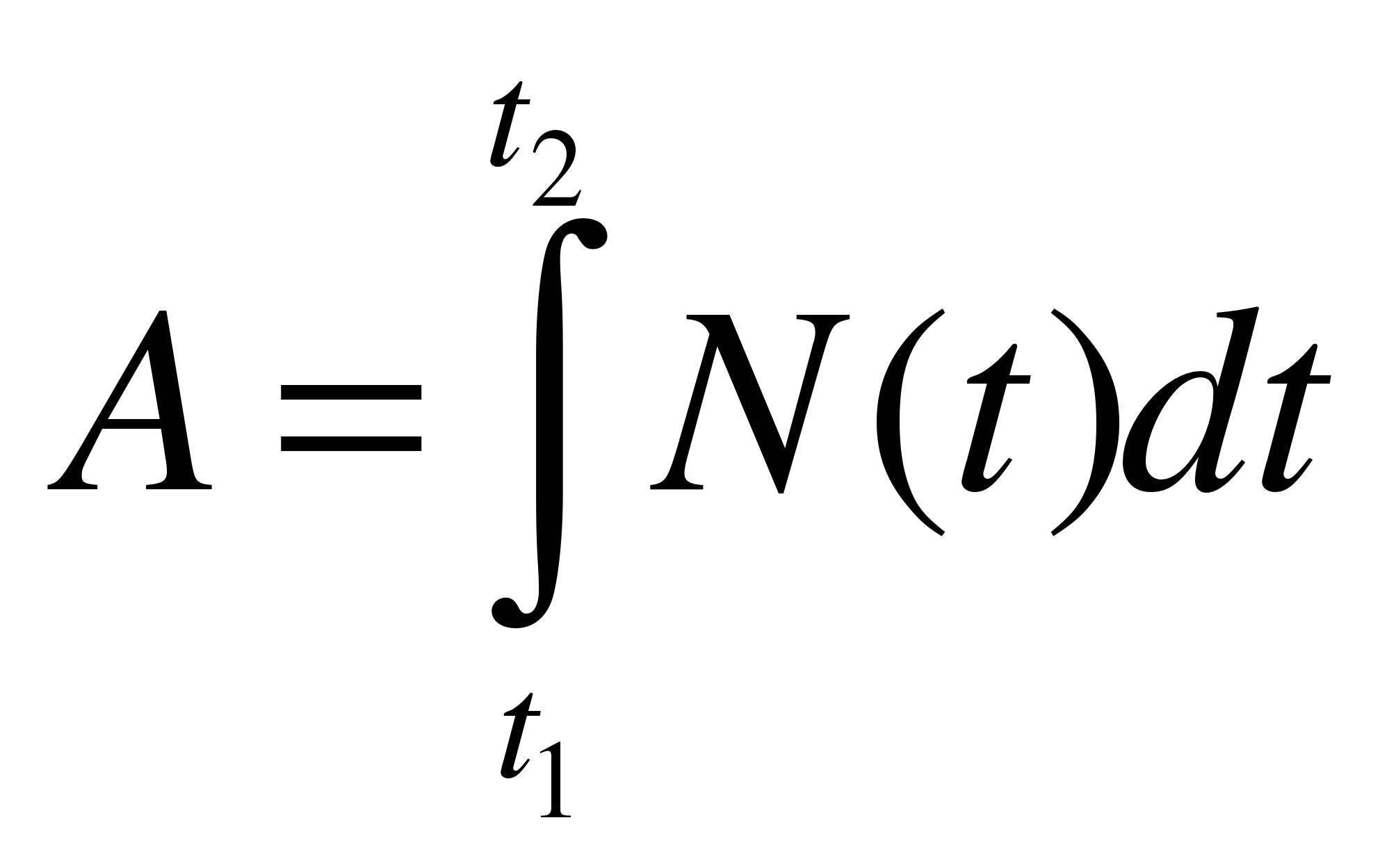
|
|
m – масса тонкого стержня,
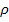 - линейная плотность - линейная плотность
|
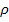 (x) = m'(x) (x) = m'(x)
|
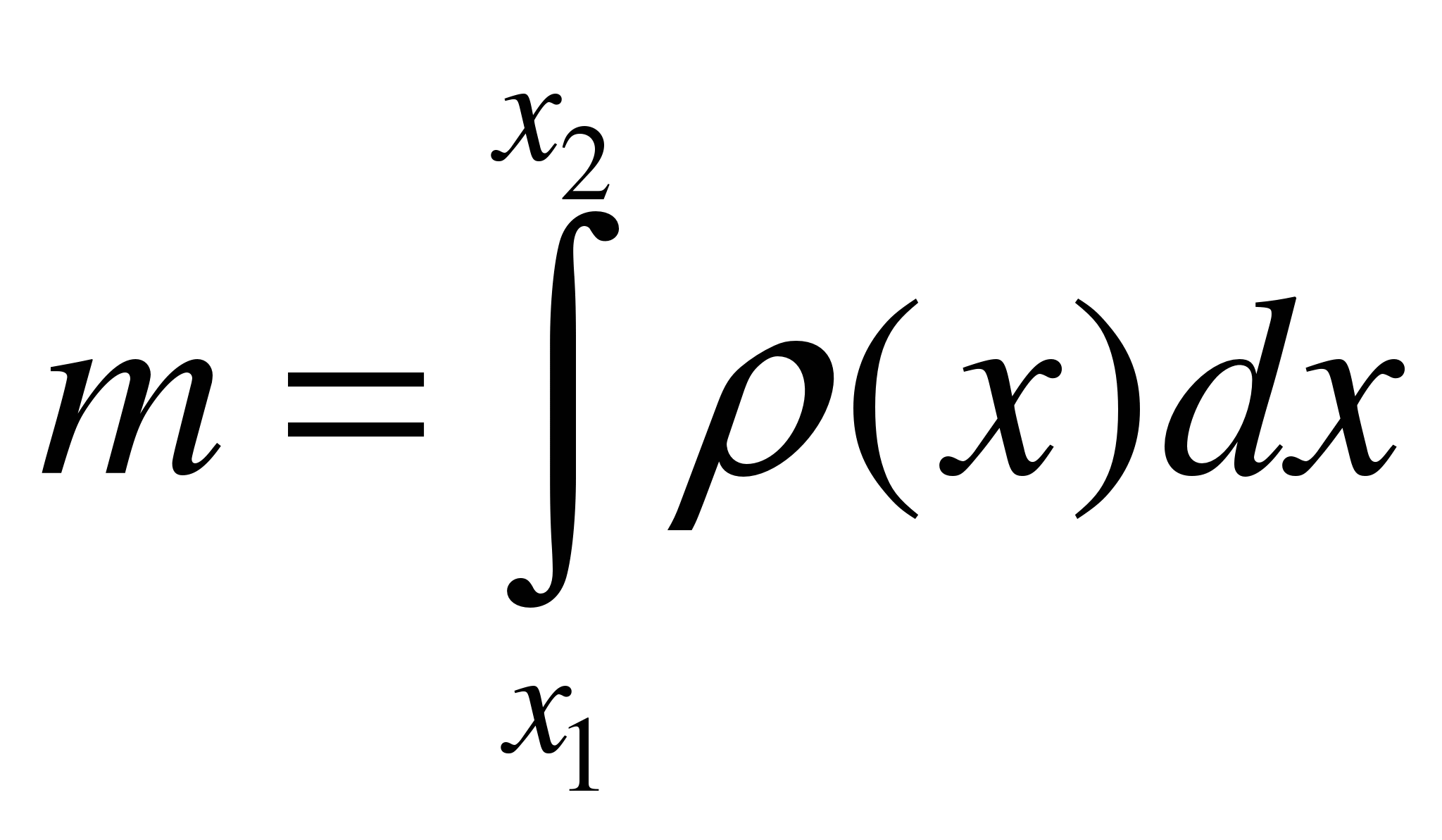
|
|
q – электрический заряд,
I –сила тока
|
I(t) = q (t) (t)
|
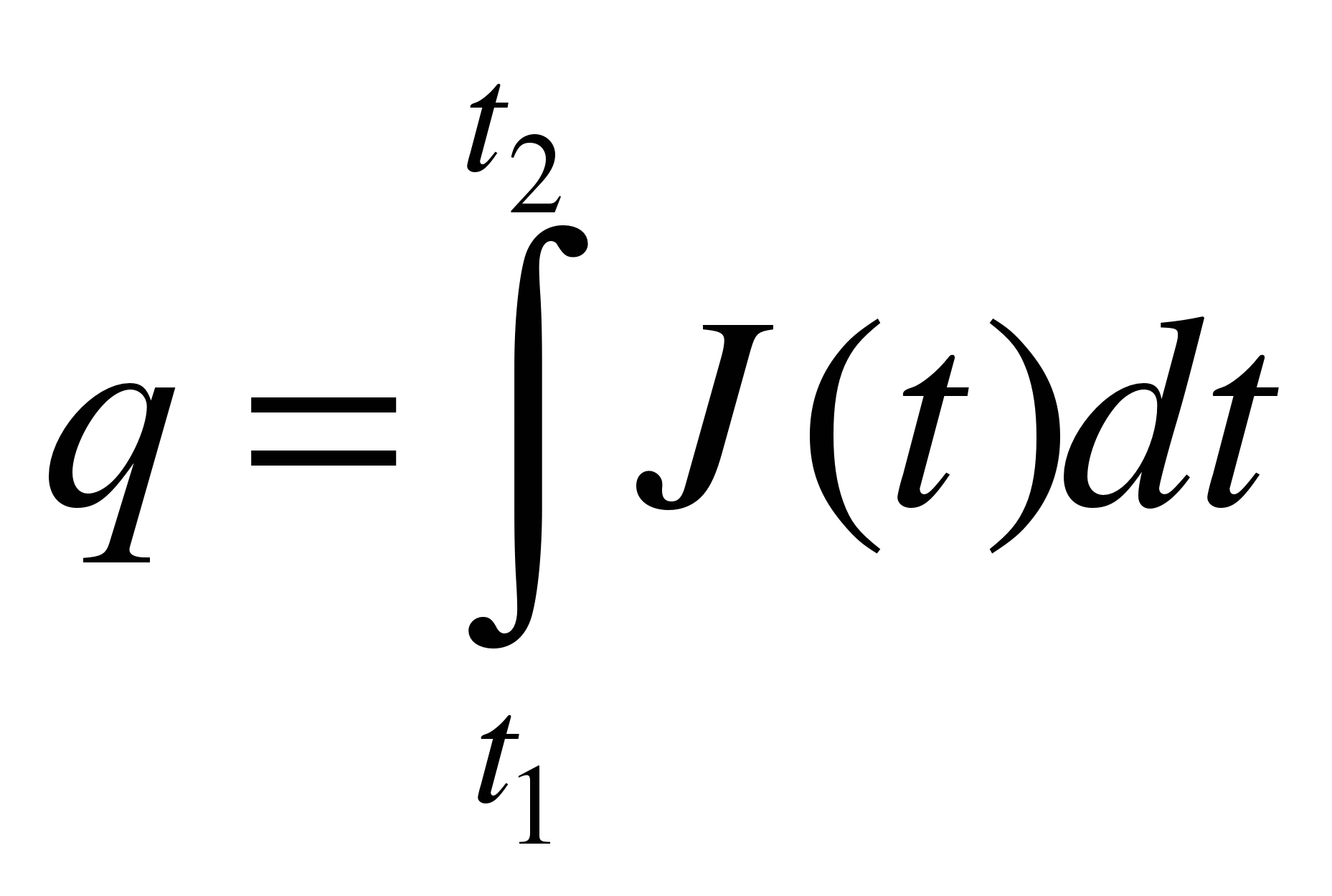
|
|
Q – количество теплоты
с - теплоемкость
|
c(t) = Q'(t)
|
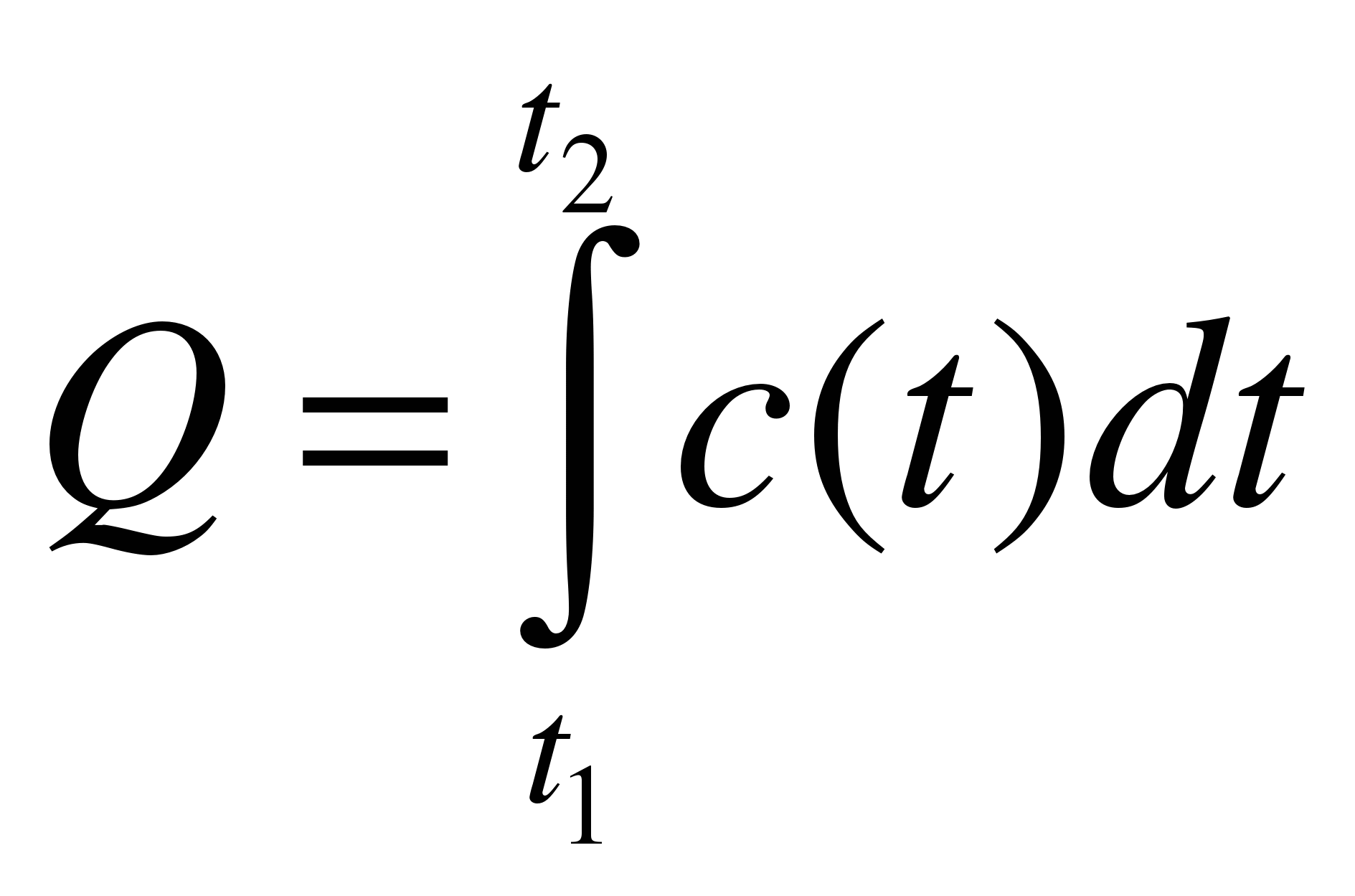
|
Правила вычисления первообразных
- Если F – первообразная для f, a G - первообразная для g, то F+G есть первообразная для f+g.
-Если F – первообразная для f, a k – постоянная, то kF есть первообразная для kf.
-Если F(x) –первообразная для f(x), ak, b – постоянные, причем k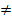 0, то есть
0, то есть 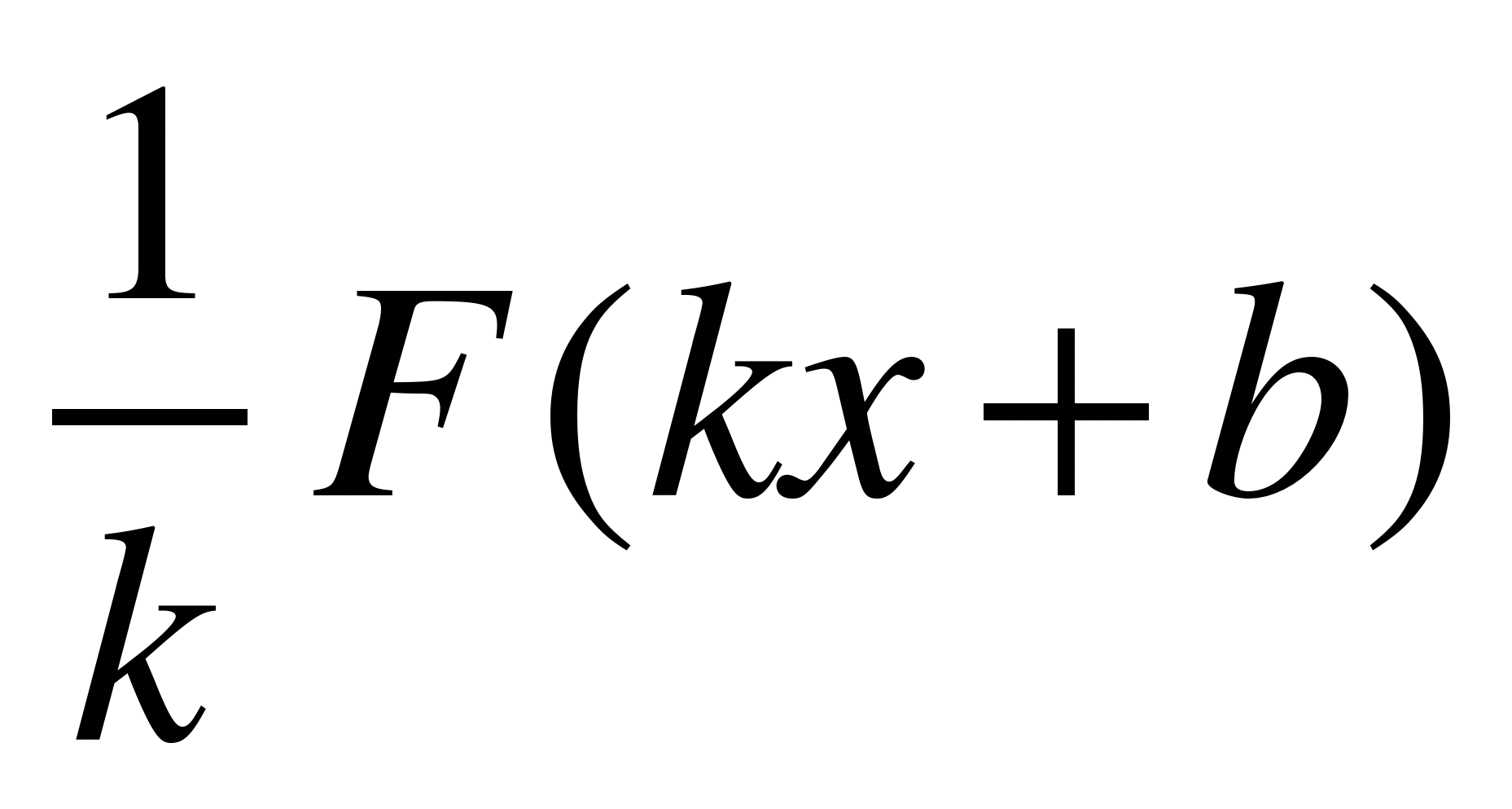 есть первообразная для f(kx+b).
есть первообразная для f(kx+b).
^ 4)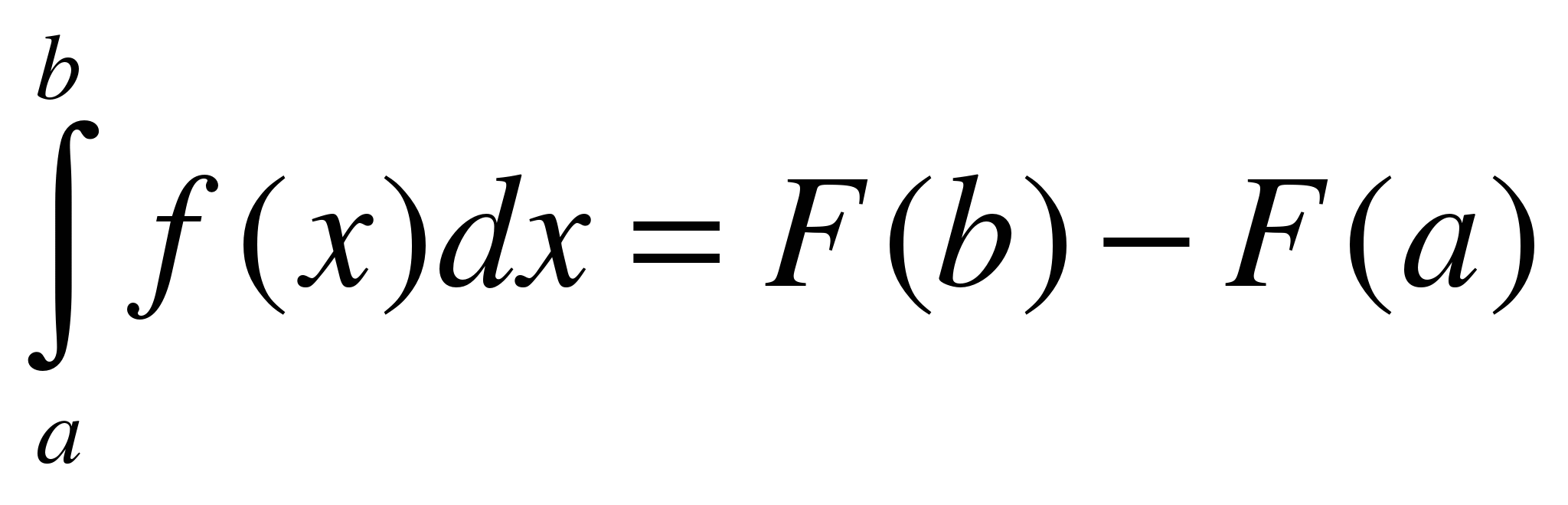 - формула Ньютона-Лейбница.
- формула Ньютона-Лейбница.
5) Площадь S фигуры, ограниченной прямыми x-a,x=b и графиками непрерывных на промежутке [a;b] функций 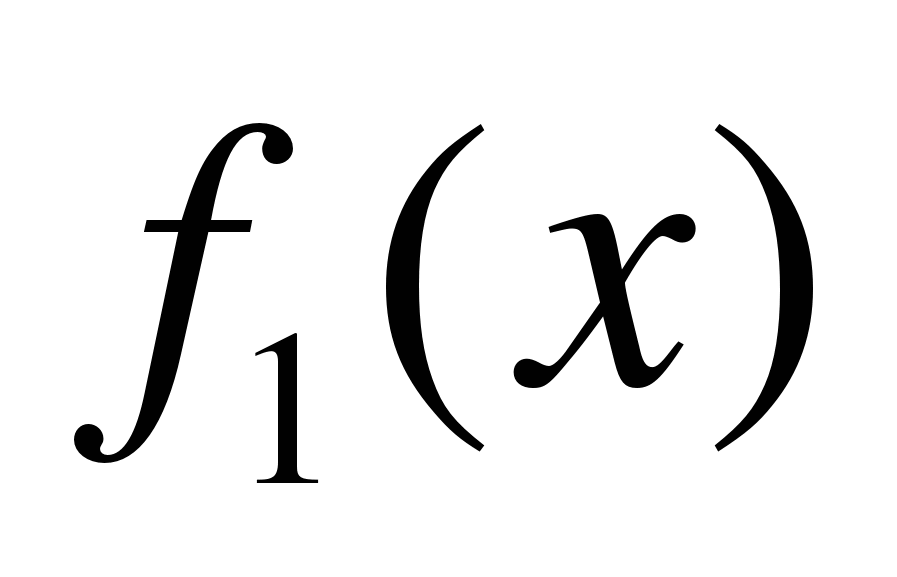 и
и 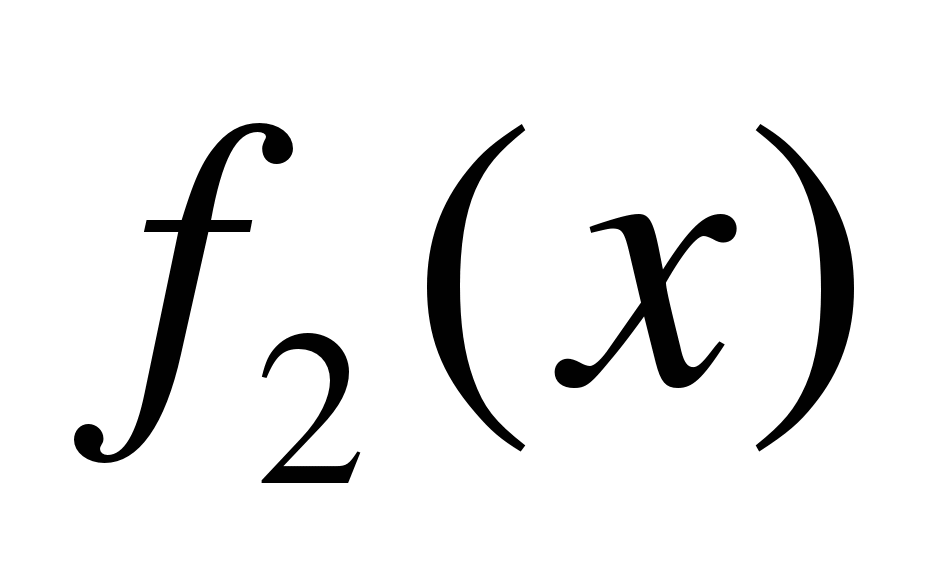 таких, что
таких, что 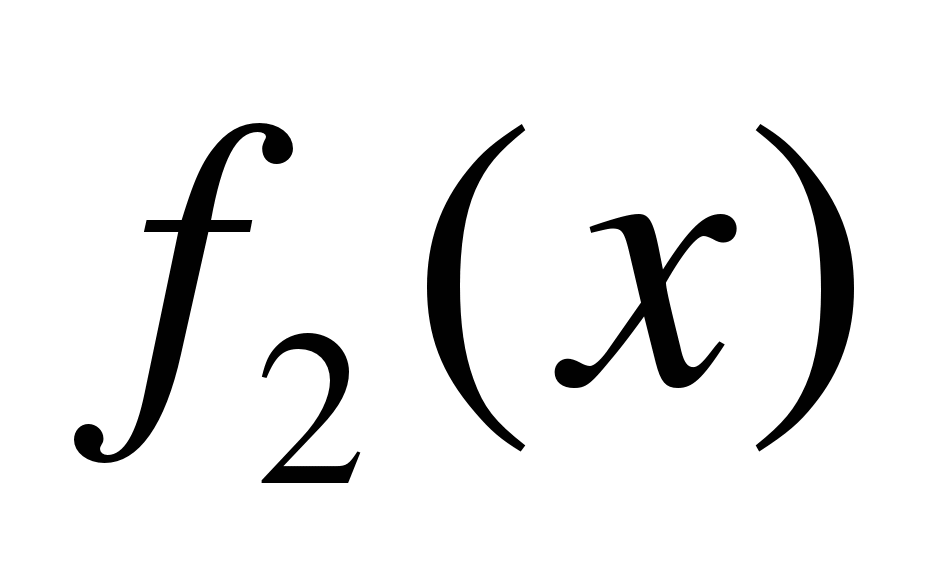
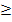
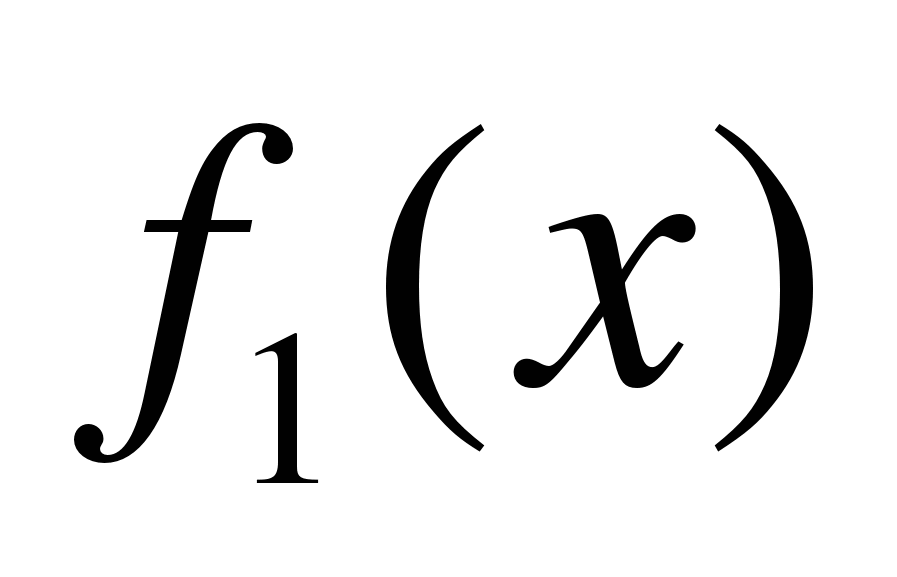 для всех x
для всех x 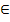 [a;b] вычисляется по формуле
[a;b] вычисляется по формуле
6) Объемы тел, образованных вращением криволинейной трапеции, ограниченной кривой y = f(x), осью Ox и двумя прямыми x = a и x = b вокруг осей Ох и Оу, вычисляются соответственно по формулам:
или
Найдите неопределенный интеграл: (устно)
|
1.
|
|
2.
|
|
3.
|
|
4.
|
|
5.
|
|
6.
|
|
7.
Ответы: |
|
1.
|
|
2.
|
|
3.
|
|
4.
|
|
5.
|
|
6.
|
|
7.
|
III Решение заданий с классом
|
1. Вычислите определенный интеграл: ( в тетрадях, один учащийся на доске)
|
|
1) ;
2); 3) .
|
Задачи по рисункам с решениями:
№ 1. Найти площадь криволинейной трапеции, ограниченной линиями y= x3, y=0, x=-3, x=1.
Решение.
0 1 0 1
-∫ х3 dx + ∫ x3 dx = - (x4/4) | + (x4 /4) | = (-3)4 /4 + 1/4 = 82/4 = 20,5
-3 0 -3 0
№3. Вычислите площадь фигуры, ограниченной линиями у=x3+1, у=0, x=0
Решение.
(3/4)
№ 5. Вычислите площадь фигуры, ограниченной линиями у= 4 -х2, у=0,
Решение. Сначала построим график, чтобы определить пределы интегрирования. Фигура состоит из двух одинаковых кусочков. Вычисляем площадь той части, что справа от оси у, и удваиваем.
(10 2/3)
№ 4. Вычислите площадь фигуры, ограниченной линиями у=1+2sin x, у=0, x=0, x=п/2
Решение.
F(x) = x - 2cosx; S = F(п/2) - F(0) = п/2 -2cosп/2 - (0 - 2cos0) = п/2 + 2
Вычислите площадь криволинейных трапеций, ограниченных графиками известных вам линий.
д)
3. Вычислите по рисункам площади заштрихованных фигур ( самостоятельная работа в парах ) Задание: вычислите площадь заштрихованной фигуры
Задание: Вычислите площадь заштрихованной фигуры
Задание: Вычислите площадь заштрихованной фигуры
III Итоги урока.
а) рефлексия: -Какие выводы от урока вы сделали для себя?
- Есть ли каждому над чем поработать самостоятельно?
- Полезен ли был для вас урок?
б) анализ работы учащихся
в) Дома: повторить, свойства все формулы первообразных, формулы нахождения площади криволинейной трапеции, объемов тел вращения. № 136 (Шыныбеков)


 Получите свидетельство
Получите свидетельство Вход
Вход


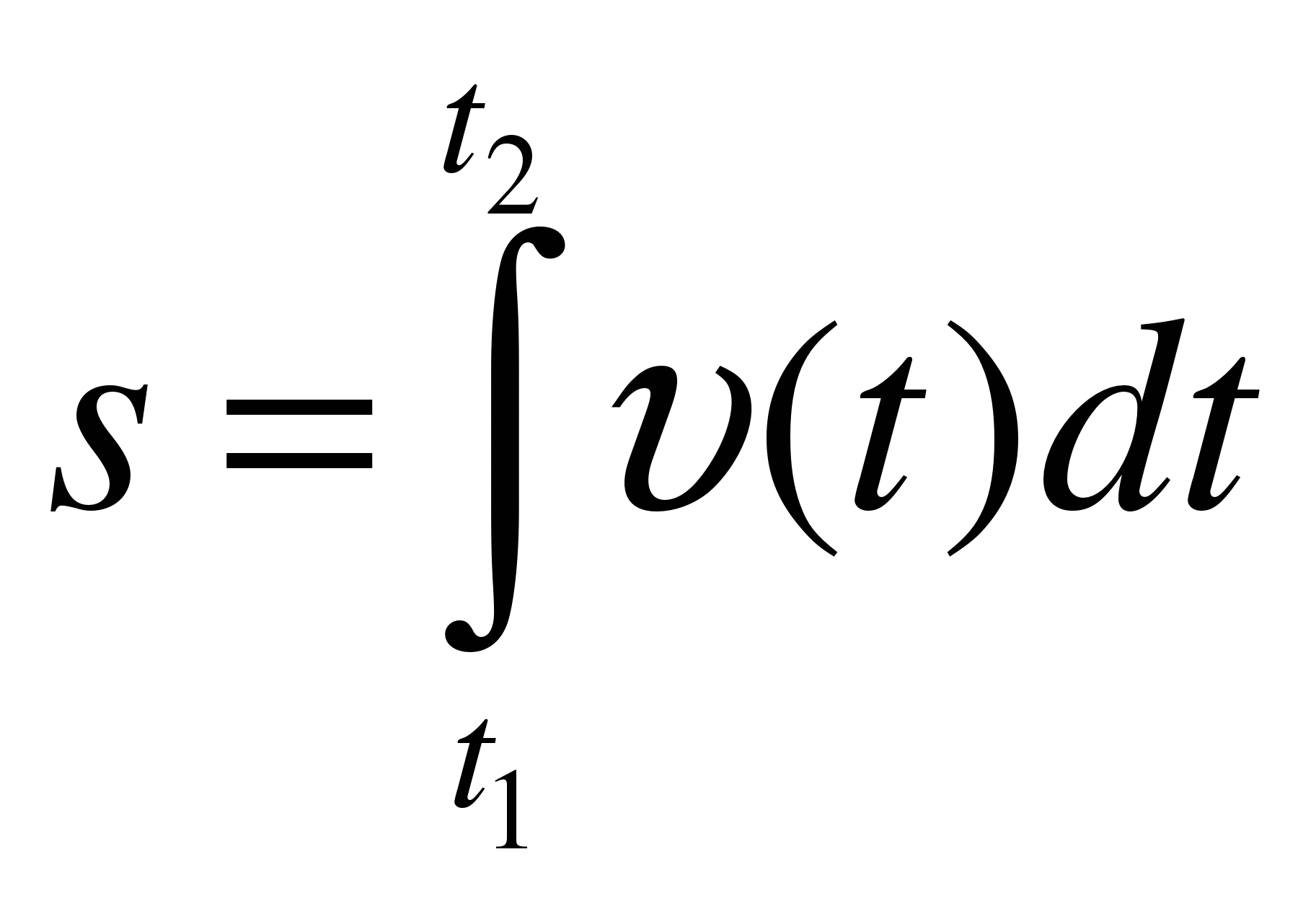
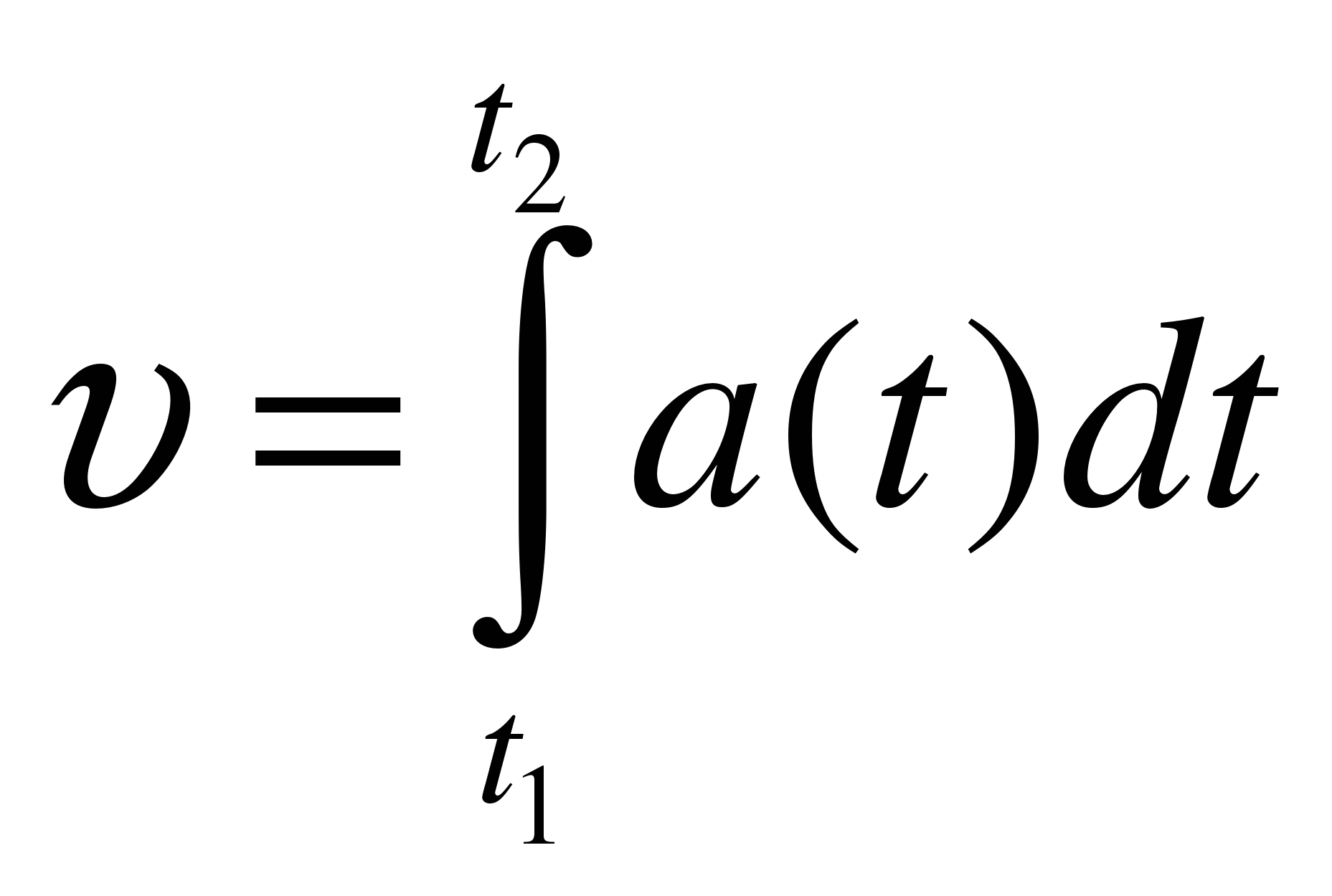
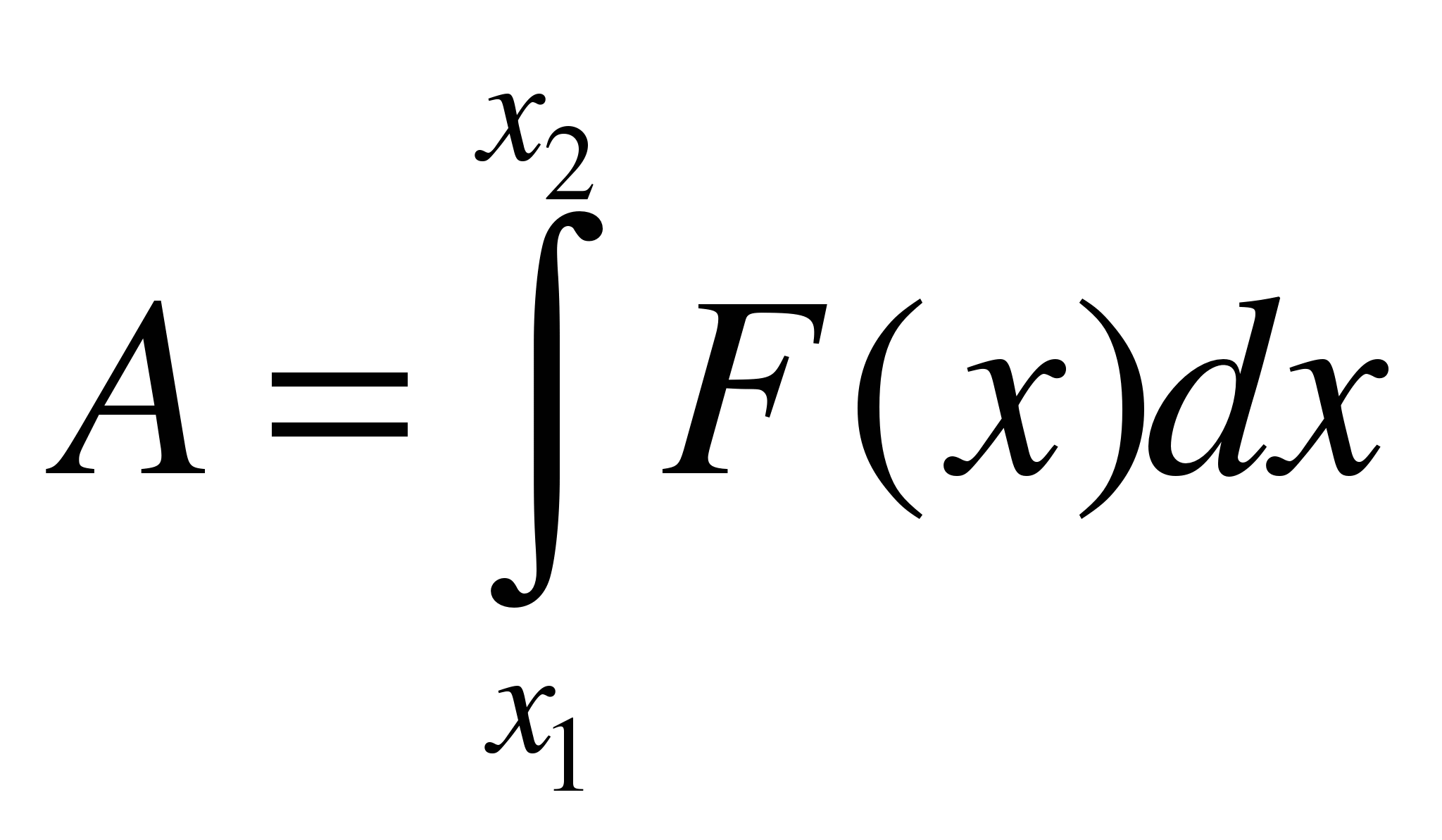
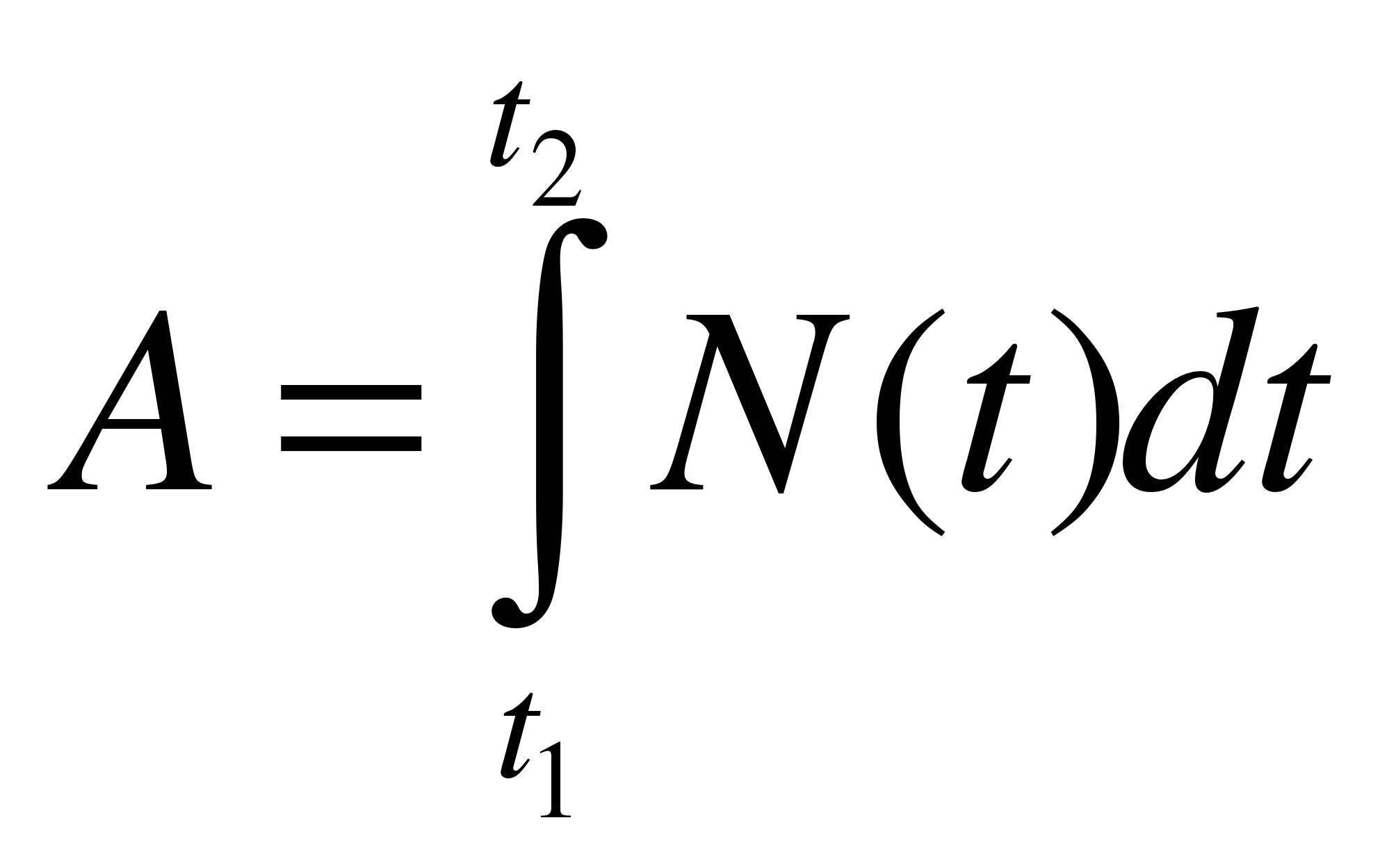
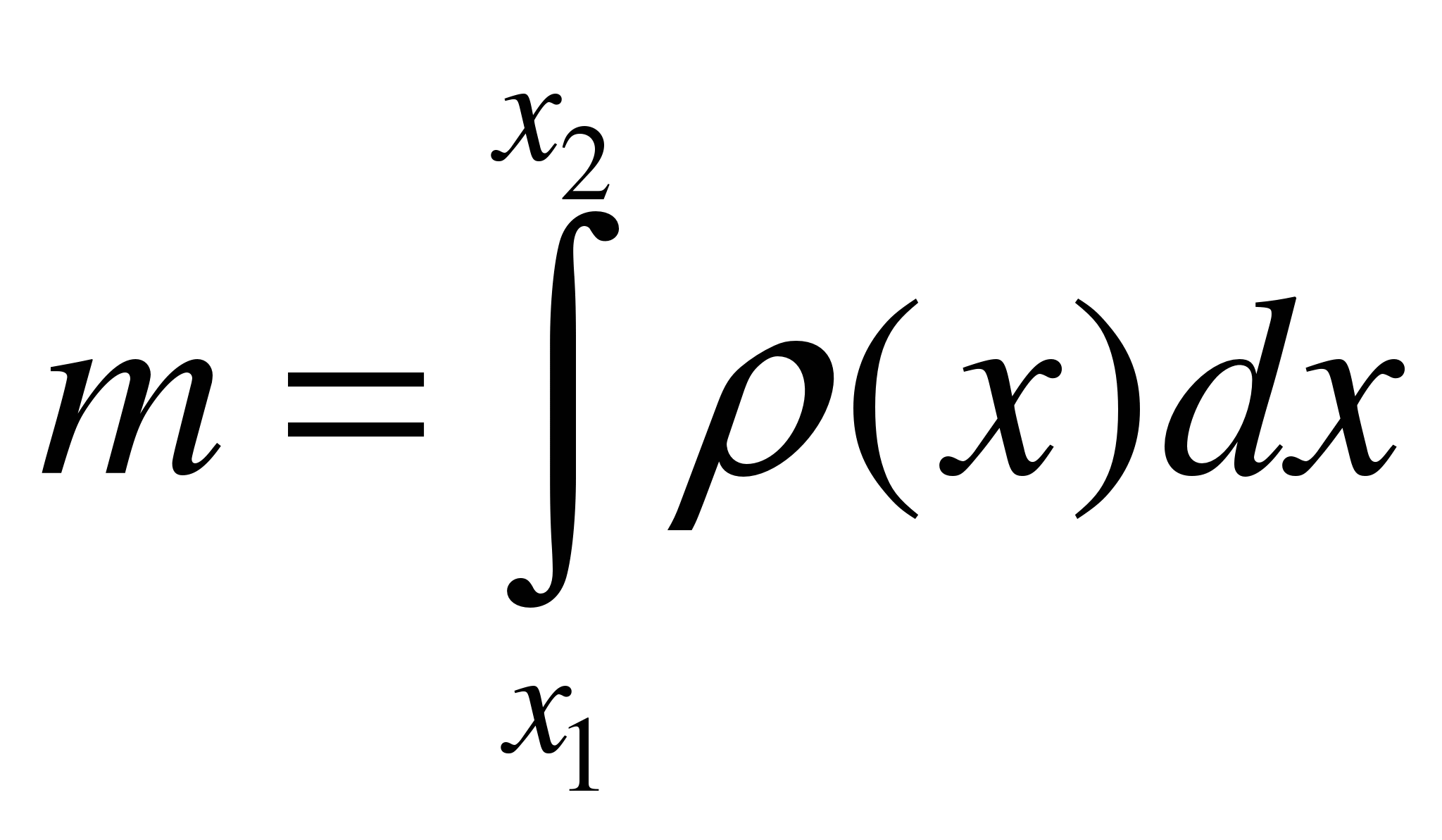
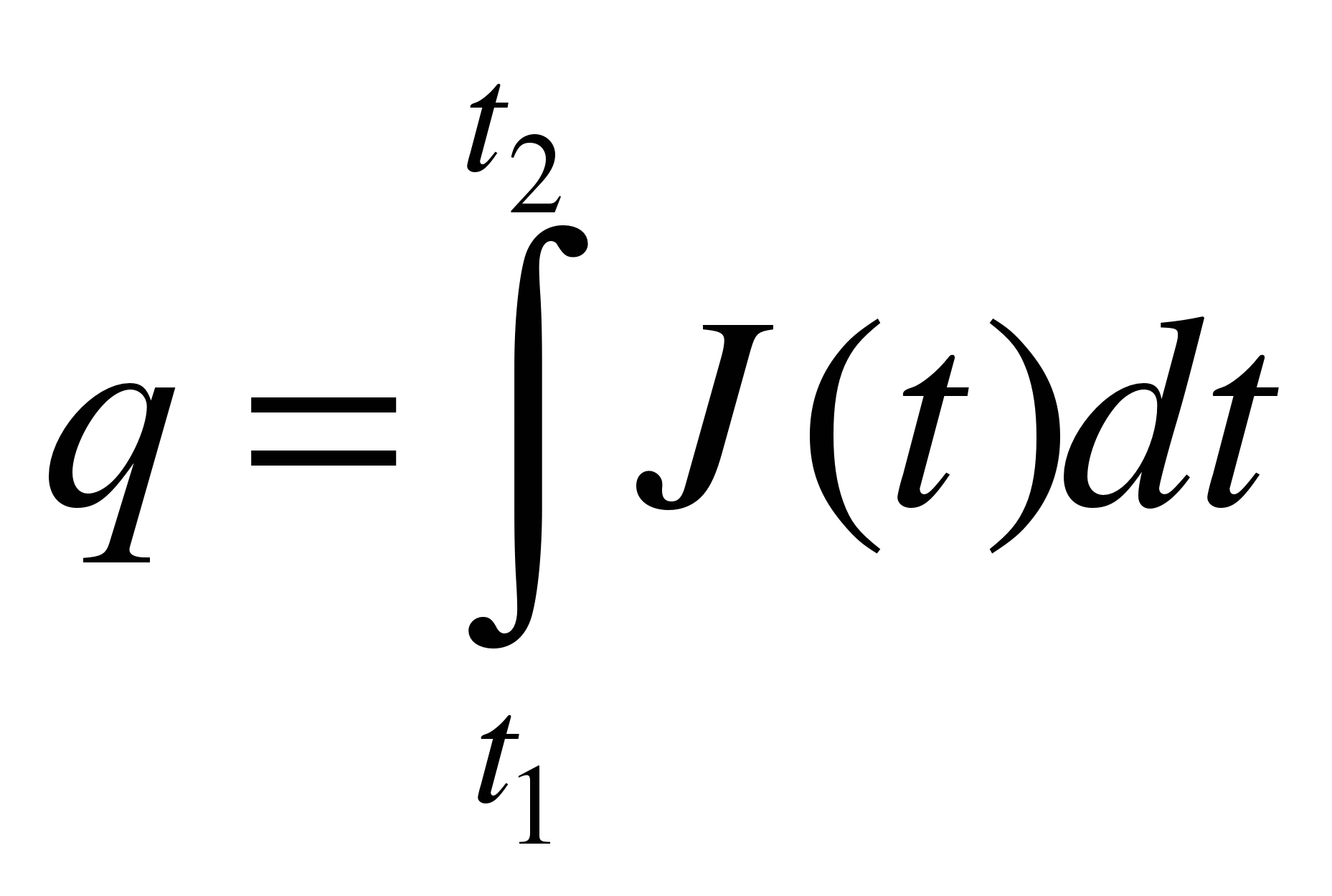
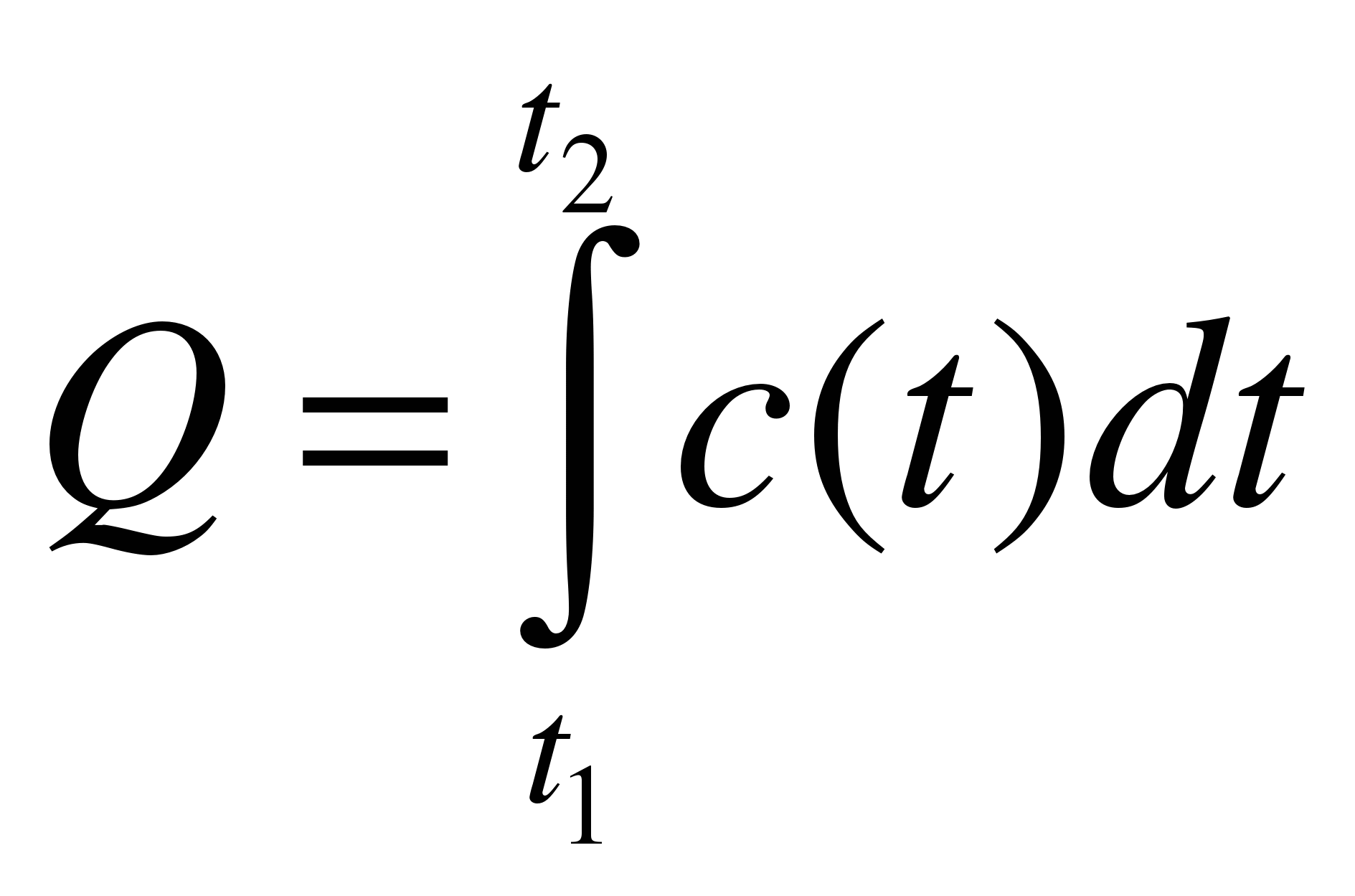









 Первообразная и интеграл (0.74 MB)
Первообразная и интеграл (0.74 MB)
 2
2 1110
1110 129
129 Нравится
0
Нравится
0





