Конспект урока
Тема: Параллельные прямые. Параллельность в пространстве.
Цели урока:
Образовательная: повторить теоретический материал; обобщить навыки решения задач по данной теме.
Развивающая: формировать умение анализировать; развитие пространственного воображения.
Воспитательная: формировать у учеников наблюдательность.
Оборудование: таблицы, карточки.
План урока
Организационный момент.
Математический диктант.
Актуализация опорных знаний.
Повторение теоретического материала.
Задачи для устной работы.
Закрепление материала.
Итоги урока.
Домашнее задание.
Ход урока
Организационный момент.
Математический диктант.
| Планиметрия | Стереометрия |
| Вариант 1 |
Какое из следующих утверждений верно? если две прямые параллельны одной и той же прямой, то они параллельны между собой (верно); через точку 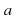 можно провести более одной прямой параллельной данной (не верно); можно провести более одной прямой параллельной данной (не верно); если две параллельные прямые пересечь третьей, то образованные при этом: внутренние накрест лежащие углы равны; соответственные углы равны; внутренние односторонние углы в сумме составляют 180° (верно).  , , 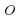 - центр пересечения. Верны ли утверждения: - центр пересечения. Верны ли утверждения:
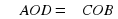 (верно); (верно);
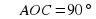 (верно); (верно);
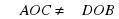 (не верно). (не верно).
| Какое из следующих утверждений верно? если прямая а параллельна некоторой прямой плоскости  , то прямая а параллельна плоскости , то прямая а параллельна плоскости  (верно); (верно); через точку  можно провести более одной плоскости параллельной данной (не верно); можно провести более одной плоскости параллельной данной (не верно); если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны (верно). Дана прямая и плоскость. Если общих точек более одной, то: прямая лежит в плоскости (верно); пряма и плоскость пересекаются (не верно); прямая параллельна плоскости (не верно). |
| Вариант 2 |
Какое из следующих утверждений верно? две прямые, не перпендикулярные одной и той же прямой, параллельны (не верно); через точку  можно провести не более одной прямой параллельной данной (верно); можно провести не более одной прямой параллельной данной (верно); если при пересечении двух прямых третьей образуются равные соответственные углы, то прямые параллельны (верно). Прямые параллельны, если: при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180° (верно); они параллельны одной и той же прямой (верно); две прямые не параллельны третьей прямой (не верно). | Какое из следующих утверждений верно? если через прямую а, параллельную плоскости  , провести плоскость, не пересекающую плоскость , провести плоскость, не пересекающую плоскость  по прямой b, то прямые a и b параллельны (не верно); по прямой b, то прямые a и b параллельны (не верно); через точку  можно провести не более одной плоскости параллельной данной (верно); можно провести не более одной плоскости параллельной данной (верно); если две параллельные плоскости пересечены третьей, то прямые пересечения параллельны (верно). Дана прямая и плоскость. Если общих точек нет, то: Прямая параллельна плоскости (верно); Прямая и плоскость пересекаются (не верно); Прямая лежит в плоскости (не верно). |
Актуализация опорных знаний.
Индивидуальная работа.
| Карточка 1 |
| В кубе 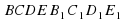 укажите прямые: укажите прямые: Параллельные ребру 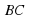 ; ; Пересекающие ребро 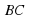 ; ; Скрещивающиеся с ребром 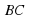 . . Через середину 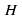 ребра ребра 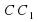 проведите прямую, параллельную проведите прямую, параллельную 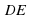 . Обоснуйте построение. . Обоснуйте построение. |
| Карточка 2 |
| Дан тетраэдр 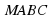 , каждое ребро которого равно 6 см. , каждое ребро которого равно 6 см.  . . 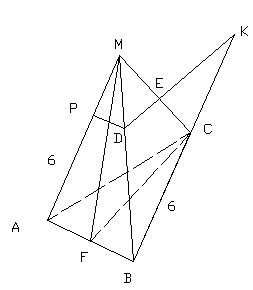
Назовите прямую, по которой пересекаются плоскости:  ; ;
MCF и  . . Найдите длину отрезка  и площадь треугольника и площадь треугольника  . ( . ( .) .) Объясните, как построена точка пересечения прямой 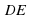 с плоскостью с плоскостью  . . Постройте точку пересечения прямой  с плоскостью с плоскостью  . . |
| Карточка 3 |
| Дано:  - куб. - куб.  . . Объясните, как построена точка пересечения прямой  с плоскостью с плоскостью  . . Объясните, как построена линия пересечения плоскостей  . . Объясните, как построить линию пересечения плоскостей  . . Вычислите длины отрезков  , если , если  . ( . ( .) .) |
| Карточка 4 |
| Даны две непересекающиеся плоскости. Докажите, что прямая, пересекающая одну из этих плоскостей, пересекает и другую. |
Повторение теоретического материала.
Вопросы:
Какие прямые в плоскости называются параллельными?
Какие параллельные в пространстве называются параллельными?
Сформулируйте теорему о существовании и единственности прямой, параллельной данной.
Сформулируйте признак параллельности прямых.
Какие прямые называются скрещивающимися?
Что значит: прямая и плоскость параллельны?
Сформулируйте признак параллельности прямой и плоскости.
Какие плоскости называются параллельными?
Сформулируйте признак параллельности плоскостей.
Докажите, что отрезки параллельных прямых, заключенные между параллельными прямыми равны.
Использование тематических таблиц «Параллельные прямые» и «Параллельность в пространстве» облегчит повторение.
Параллельные прямые
| Признаки параллельности (прямая теорема) | Рисунок |
| Если  , то , то  . . Следствие: если  . . | 

|
| Если  , то , то  . . | 
|
| Если  , то , то  . . | 
|
Параллельность в пространстве
| Взаимное расположение |
| прямых |
| 
| 
| 
|
| 
 | 
 |   скрещиваются скрещиваются
|
| Прямой и плоскости |
| Общих точек более одной  прямая лежит в плоскости (плоскость проходит через прямую) прямая лежит в плоскости (плоскость проходит через прямую) | Общая точка только одна  Прямая и плоскость пересекаются Прямая и плоскость пересекаются | Общих точек нет  Прямая параллельна плоскости Прямая параллельна плоскости |
| Плоскостей |
| Общие точки есть  Плоскости пересекаются Плоскости пересекаются | Общих точек нет  Плоскости параллельны Плоскости параллельны |
| Признаки параллельности |
| 

| 


| 




|
| Свойства |
| прямых | Прямой и плоскости | плоскостей |
| 


| 

| 





|
Задачи для устной работы.
Прямая не параллельна плоскости. Каким может быть их взаимное расположение?
Параллельны ли прямая и плоскость:
Если они не пересекаются;
Прямая не лежит в данной плоскости?
Найдется ли в плоскости  прямая, параллельная прямой
прямая, параллельная прямой 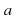 :
:
Если прямая ;
Прямая 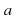 не параллельна плоскости
не параллельна плоскости  ?
?
Плоскость  проходит через прямую
проходит через прямую  и пересекает плоскость
и пересекает плоскость  по прямой
по прямой  так, что прямые
так, что прямые  не пересекаются. Выясните взаимное расположение прямой
не пересекаются. Выясните взаимное расположение прямой  и плоскости
и плоскости  .
.
Две плоскости пересекаются по прямой  . Прямая
. Прямая  лежит в одной из плоскостей и не параллельна другой плоскости. Параллельны ли прямые
лежит в одной из плоскостей и не параллельна другой плоскости. Параллельны ли прямые  ?
?
Две плоскости пересекаются по прямой а. Прямая b лежит в одной из плоскостей и параллельна прямой а. Параллельна ли прямая b другой плоскости?
Прямая а лежит в плоскости  и параллельна плоскости
и параллельна плоскости  . Прямая b лежит в плоскости
. Прямая b лежит в плоскости  и параллельна плоскости
и параллельна плоскости  . Плоскости
. Плоскости  и
и  пересекаются по прямой с. Выясните взаимное расположение прямых а и b.
пересекаются по прямой с. Выясните взаимное расположение прямых а и b.
Верно ли утверждение:
а) если одна из двух параллельных прямых параллельна плоскости, то вторая прямая не пересекает эту плоскость;
б) если одна из двух прямых параллельна плоскости, а вторая пересекает эту плоскость, то прямые параллельны?
9. Прямые с и b параллельны. Прямая с имеет общую точку с плоскостью  , а прямая b не имеет общих точек с этой плоскостью. Выясните взаимное расположение прямой с и плоскости
, а прямая b не имеет общих точек с этой плоскостью. Выясните взаимное расположение прямой с и плоскости  .
.
10. Каково взаимное расположение двух плоскостей, если третья плоскость пересекает их по прямым:
а) имеющим общую точку; б) не имеющим общих точек?
Две стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть ее боковыми сторонами?
Каким может быть взаимное расположение двух прямых, если эти прямые пересекают две параллельные плоскости и их отрезки, заключенные между плоскостями, не равны?
Две плоскости пересечены двумя параллельными прямыми. Выясните взаимное расположение плоскостей, если отрезки данных прямых, заключенные между этими плоскостями, не равны.
Закрепление материала.
Математический диктант
Выясните взаимное расположение прямых  . (Пересекаются.)
. (Пересекаются.)
 - куб. Каково взаимное расположение прямых
- куб. Каково взаимное расположение прямых  ? (Скрещиваются.)
? (Скрещиваются.)
 - куб. чему равен угол между
- куб. чему равен угол между  ?
?
 ;
;
 ;
;
 ;
;
 ;
;
Определить нельзя.
Прямые a и b скрещиваются с прямой c. Что можно сказать о прямых a и b?
Точка  не лежит в плоскости треугольника
не лежит в плоскости треугольника  ,
,  - середина
- середина  . Каково взаимное расположение прямых
. Каково взаимное расположение прямых  ? (Скрещиваются.)
? (Скрещиваются.)
Каким может быть взаимное расположение прямых a и b, если через прямую a можно провести плоскость, параллельную прямой b?
Параллелограммы  лежат в разных плоскостях, какую фигуру представляет собой
лежат в разных плоскостях, какую фигуру представляет собой  . (Параллелограмм.)
. (Параллелограмм.)
Отрезки  и
и  лежат соответственно в параллельных плоскостях
лежат соответственно в параллельных плоскостях  . Что можно сказать о взаимном расположении прямых
. Что можно сказать о взаимном расположении прямых  ?
?
Итоги урока.
Домашнее задание.
Повторить теорию, выполнить тест по теме: «Параллельность в пространстве».
Понятия, не требующие доказательства:
1. Перпендикулярные прямые в пространстве. Примеры двух перпендикулярных прямых в пространстве, содержащих ребра правильной треугольной пирамиды. Вычисление расстояния между двумя скрещивающимися перпендикулярными прямыми. Пример вычисления расстояния между скрещивающимися прямыми, содержащими боковое ребро правильной треугольной призмы и ребро ее основания.
Перпендикулярные прямые. Перпендикулярность прямой и плоскости в пространстве. Теорема о трех перпендикулярах (формулировка и пояснение рисунком).
Перпендикуляр и наклонная, Расстояние точки до плоскости: Примеры перпендикуляра к плоскости основания призмы; пирамиды. Высоты призмы и пирамиды.
4.Перпендикулярность прямой и плоскости в пространстве, Признак перпендикулярности прямой и плоскости (формулировка).
5. Перпендикулярность прямой и плоскости в пространстве. Свойство прямых, перпендикулярных одной плоскости (формулировка).
6.Перпендикулярность прямой и плоскости в пространстве. Свойство плоскости, перпендикулярной одной из двух параллельных прямых (формулировка).
7.Взаимное расположение двух прямых в пространстве. Угол между прямыми в пространстве. Пример нахождения величины угла между скрещивающимися прямыми на модели правильной треугольной призмы.
8.Взаимное расположение прямой и плоскости. Угол между прямой и плоскостью. Пример нахождения величины угла между прямой и плоскостью на модели правильной четырехугольной призмы.
9. Взаимное расположение двух плоскостей. Угол между двумя плоскостями. Пример нахождения величины угла между двумя плоскостями на модели куба.
Понятия, требующие доказательства:
1. Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах (с доказательством).
Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости (с доказательством).
Перпендикулярность плоскостей. Признак перпендикулярности двух плоскостей (с доказательством).
Тест «Параллельность в пространстве».
1. Через вершины параллелограмма ABCD, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пресекающие вторую плоскость в точках  , тогда
, тогда  представляет собой:
представляет собой:
параллелограмм;
трапецию;
произвольный четырехугольник;
прямоугольник;
ромб.
Точка  лежит между параллельными плоскостями
лежит между параллельными плоскостями  . прямые a и b, проходящие через точку К, пересекают плоскость
. прямые a и b, проходящие через точку К, пересекают плоскость  в точках
в точках  , а плоскость
, а плоскость  - в точках
- в точках  соответственно. Найдите
соответственно. Найдите  , если
, если  : .
: .
3,75 см;
5 см;
7,5 см;
10 см;
12,5 см.
Сторона  треугольника ABC лежит в плоскости
треугольника ABC лежит в плоскости  . Через середину стороны
. Через середину стороны  - точку
- точку  - проведена плоскость
- проведена плоскость , параллельная плоскости
, параллельная плоскости  , она пересекает
, она пересекает 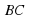 в точке
в точке  . Найдите
. Найдите  , если PE
, если PE .
.
3,5 см;
7 см;
10,5 см;
14 см;
Определить нельзя.
Через концы отрезка  , не пересекающего плоскость
, не пересекающего плоскость  и точку
и точку  - середину этого отрезка, проведены параллельные прямые, пересекающие плоскость
- середину этого отрезка, проведены параллельные прямые, пересекающие плоскость  в точках
в точках  соответственно. Найдите длину отрезка
соответственно. Найдите длину отрезка 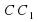 , если
, если  .
.
6;
9;
 ;
;
 ;
;
В параллелограмме ABCD точки  принадлежат сторонам
принадлежат сторонам  , причем
, причем  . Через эти точки проведена плоскость
. Через эти точки проведена плоскость  так, что
так, что  , тогда:
, тогда:
 ;
;
 ;
;
 ;
;
;
Плоскость  совпадает с плоскостью параллелограмма.
совпадает с плоскостью параллелограмма.
На рисунке точки  - середины соответственно сторон
- середины соответственно сторон  .
.  . Найдите периметр четырехугольника
. Найдите периметр четырехугольника  , если
, если  .
.
18;
36;
28;
26;
Определить нельзя.
На сторонах  треугольника
треугольника  взяли соответственно точки
взяли соответственно точки  так, что , провели плоскость через точки
так, что , провели плоскость через точки  параллельно к отрезку
параллельно к отрезку 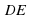 . Найдите длину отрезка
. Найдите длину отрезка 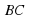 .
.
7,5 см;
 см;
см;

Определить нельзя;
4,6 см.
На рисунке плоскость параллельна стороне  треугольника
треугольника  , пересекает его стороны в точках
, пересекает его стороны в точках  . Найдите длину
. Найдите длину  , если точка
, если точка  - середина
- середина  .
.

определить нельзя;
10;
5;
 ;
;
 .
.
На рисунке плоскость, параллельная основаниям трапеции  , пересекает стороны
, пересекает стороны  в точках
в точках  соответственно. Найдите длину
соответственно. Найдите длину  , если точка
, если точка  - середина .
- середина .
определить нельзя;
16;
11;
13;
8.
На рисунке точки  - середины соответственно сторон
- середины соответственно сторон  .
.  . Найдите периметр четырехугольника .
. Найдите периметр четырехугольника .
18;
26;
28;
36;
определить нельзя.
На сторонах  треугольника
треугольника  взяли соответственно точки
взяли соответственно точки  так, что , провели плоскость через точки
так, что , провели плоскость через точки  параллельно к отрезку
параллельно к отрезку  . Найдите длину отрезка
. Найдите длину отрезка  .
.
9 см;
10 см;
4 см;
определить нельзя;
3,6 см.
Сторона  треугольника
треугольника  лежит в плоскости
лежит в плоскости  . Через середину стороны
. Через середину стороны  – точку
– точку  – проедена плоскость
– проедена плоскость  , параллельная плоскости
, параллельная плоскости  и пересекающая
и пересекающая 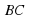 в точке
в точке  . Найдите
. Найдите  , если
, если  см.
см.
10 см;
5 см;
2,5 см;
20 см;
Определить нельзя.
Параллельные плоскости  пересекают стороны угла
пересекают стороны угла  в точках
в точках  соответственно. Найдите
соответственно. Найдите
 см.
см.
1,5 см;
3 см;
6см;
9 см;
4 см.
Точка  не лежит в плоскости треугольника
не лежит в плоскости треугольника  , точки
, точки  - середины отрезков
- середины отрезков  соответственно. Найдите площадь треугольника
соответственно. Найдите площадь треугольника  , если площадь треугольника
, если площадь треугольника  равна
равна  .
.
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
:
| Задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Ответы | b | a | b | e | b | D | d |
| Задания | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Ответы | e | e | d | b | b | b | c |
Литература:
Атанасян, Л.С. Геометрия. 7-9 классы: учеб. для общеобразовательных учреждений/Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др. – 19-е изд. – М. : Просвещение, 2009 – 384 с.: ил.
Атанасян, Л.С. Геометрия. 10-11 классы: учеб. для общеобразовательных учреждений: базовый и профильный уровни/Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др. – 18-е изд. – М. : Просвещение, 2009 – 255 с. : ил.
Беденко, Н.К. Уроки геометрии на втором курсе средних профтехучилищ: Методическое пособие для средних проф.-тех. училищ. – М.: Высш. шк., 1988 – 96 с.: ил.
Далингер, В.Ф. Методика реализации внутрипредметных связей при обучении математике: Кн. для учителя/В.Ф. Далингер. – М.: Просвещение, 1991 – 80 с.: ил.
Ершова, А.П. устные проверочные и зачетные работы по геометрии для 10-11 класса. – М.: Илекса, - 2005, - 112 с.
Крутова, И.А. Математика в таблицах и схемах. Для школьников и абитуриентов/Крутова И.А. – «Полиграфуслуги», 2006. – 224 с.
Лысенко, Ф.Ф. Математика. Подготовка к ЕГЭ-2010/Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону: Легион-М., 2009. – 480 с.
Лященко, Е.И. Лабораторные и практические работы по методике преподавания математики: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов/Е.И. Лященко, К.В. Зобкова, Т.Ф. Кириченко и др.; Под ред. Е.И. Лященко. – М.: Просвещение, 1988. – 223 с.: ил.


 Получите свидетельство
Получите свидетельство Вход
Вход


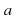 можно провести более одной прямой параллельной данной (не верно);
можно провести более одной прямой параллельной данной (не верно); ,
, 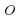 - центр пересечения. Верны ли утверждения:
- центр пересечения. Верны ли утверждения: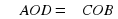 (верно);
(верно);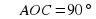 (верно);
(верно);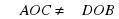 (не верно).
(не верно). , то прямая а параллельна плоскости
, то прямая а параллельна плоскости 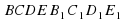 укажите прямые:
укажите прямые: ;
; ребра
ребра 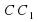 проведите прямую, параллельную
проведите прямую, параллельную 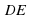 . Обоснуйте построение.
. Обоснуйте построение.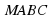 , каждое ребро которого равно 6 см.
, каждое ребро которого равно 6 см. 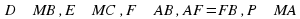 .
.
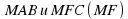 ;
;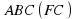 .
.








 Параллельные прямые. Параллельность в пространстве (97.14 КB)
Параллельные прямые. Параллельность в пространстве (97.14 КB)
 0
0 1750
1750 101
101 Нравится
0
Нравится
0




