| Предмет | Математика |
| Ф.И.О. учителя |
|
| Учебник | Математика 6 кл. Алматы «Мектеп» 2018 |
| Тема урока | Отношение двух чисел. Процентное отношение двух чисел |
| Цели обучения (кратко) | 6.1.2.1 усвоить понятие отношения чисел 6.1.2.2 находить отношение, обратное данному отношению 6.1.1.1 понимать, что показывает отношение двух чисел 6.5.2.1 читать и записывать отношения двух чисел |
| Порядок действий | Ресурсы |
| Изучи
Ответь
Выполни | Просмотрите видео, запишите примеры в тетрадь https://yandex.ru/search/?text=освобождение%20от%20иррациональности%20в%20знаменателе%20дроби%208%20класс%20конспект%20урока&clid=2337486-33&win=391&lr=189326 Изучи параграф 1 стр. 18-20 учебника Частное двух чисел называется отношением этих чисел. Отношение двух чисел показывает, во сколько раз одно число больше или меньше другого, или какую часть от большего числа составляет меньшее число Отношение чисел.
Как уже отмечалось, частное от деления одного числа на другое называется также их отношением. Таким образом, частное и отношение обозначают одно и то же понятие. Однако, когда говорят , имеют в виду одно число, полученное в результате деления двух данных чисел. Когда же говорят , имеют в виду пару чисел, соединённых знаком деления.
ПРИМЕР:
Если разделить 10 на 2, получим:
10 : 2 = 5.
В данном случае говорят, что частное от деления 10 на 2 равно 5, говорят также, что отношение 10 к 2 равно 5. Но само отношение данных чисел записывают в виде 10 : 2, или 10/2. Понятно, что числа 10 : 2 и 5 равны, поэтому и говорят, что отношение – то же самое, что и частное.
Отношением называется число, которое показывает, во сколько раз одна величина больше другой, или какую часть одна величина составляет от другой.
Числа a і b называются членами отношения. Первый член a называется предыдущим, а второй член b – последующим.
ПРИМЕР:
В отношении
4 : 5,
число 4 есть предыдущий член, 5 – последующий.
Так как отношение двух чисел с помощью деления, то для него справедливы все свойства частного.
Основное свойство отношения.
Значение отношения не изменится, если его члены умножить или разделить на одно и то же число, отличное от нуля.
Членами отношения могут быть любые числа, только последующий член не может быть равен нулю. Поэтому возможны и такие отношения:
Чтобы найти отношение одноименных величин (длин, масс и т. д.), необходимо выразить их в одной и той же единице измерения – в противном случае полученный результат для сравнения величин использовать нельзя.
ПРИМЕР:
Найти отношения 73 см к 2,92 м:
Сокращение членов отношения и замена отношения дробных чисел отношением целых чисел.
Используя основное свойство отношения, выполняем два преобразования:
– сокращение членов отношения; – замену отношения дробных чисел отношением целых чисел.
Как это выполняется, видно из следующих примеров.
ПРИМЕР:
Сократить члены отношения:
48 : 32 = 3 : 2.
ПРИМЕР:
Заменить отношение дробных чисел отношением целых чисел:
11/2 : 2/3 = 3/2 : 2/3 = 9/6 : 4/6 = 9 : 4.
Мы привели дроби к общему знаменателю, а затем умножили предыдущий и последующий члены отношения на их общий знаменатель (на 6).
При сравнении величин мы можем найти два таких отношения, в которых предыдущий член одного будет следующим членом другого и наоборот. Такие два отношения называются обратными. Произведение обратных отношений равно единицы.
Отношение величин.
Отношение однородных величин равно отношению чисел, получающихся при измерении этих величин одной и той же единицей; оно не зависит от выбора единицы измерения.
Иногда говорят об отношении разнородных величин. Например, говорят об отношении пути ко времени, массы к объёму и т. д. отношение разнородных величин есть величина. Так, отношение пути ко времени есть скорость, отношение массы к объёму – плотность и т. д. значение отношения разнородных величин зависит от выбора единицы измерения.
ПРИМЕР:
Если путь равен 20 м, а время, затраченное на его прохождение, равно 5 сек, то отношение пути ко времени равно 4 м/сек. Оно выражает скорость движения в м/сек. Если тот же путь измерить в километрах, а время – в часах, то отношение пути ко времени будет равно:
0,02 : 1/720 = 14,4 (км/час).
Оно выражает ту же скорость в км/час:
4 м/сек = 14,4 км/час.
Задача—рассказ. Всем нам приходилось пить чай из чашек разного размера, при этом сахар каждый добавляет по своему вкусу, добиваясь привычного ощущения сладости независимо от емкости посуды. Например, если ты каждое утро выпиваешь250г чая, в котором растворено3 ложки сахара, то есть 30г, то отношение 30/250, которое равно 3/25, и будет характеризовать твой ,,сахарный вкус”. Число 3/25 показывает какую часть от массы напитка составляет масса сахара. А если ты захочешь выпить 400г чая, то, чтобы он был привычного вкуса, в нем должно быть растворено 400*3/25=48(г) сахара. Запишем в процентах: 3/25=0,12=121%. Число 12 показывает, сколько процентов в выпитом чае составляет сахар. Это число называют процентным отношением массы сахара к массе чая. Процентное отношение двух чисел — это их отношение, выраженное в процентах. Оно показывает, сколько процентов одно число составляет от другого.
Чтобы выразить отношение (частное) в процентах, надо значение частного умножить на 100 и к полученному значению произведения приписать знак процента Чтобы найти, сколько процентов составляет одно число от другого, нужго: 1)первое число разделить на второе; 2)полученное значение частного выразить в процентах
Внимательно изучи задачи с решением и запиши в тетрадь
Реши задачи 1. Какой процент жирности молока, если из 250 кг молока получили 15 кг жиру ?
а) 9%;
2. Сколько процентов от часа составляют 24 мин. ?
а) 40%;
3. Какой процентный состав соли в растворе, если 400 г раствора содержит 36 г соли ?
а) 12%;
По учебнику № 101, 102
Все задания старайся сделать сам. Если возникнут трудности, можешь обратиться ко мне за помощью. Удачи! |

 Получите свидетельство
Получите свидетельство Вход
Вход



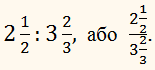
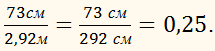









 Отношение двух чисел. Процентное отношение двух чисел (27.7 KB)
Отношение двух чисел. Процентное отношение двух чисел (27.7 KB)
 0
0 442
442 13
13 Нравится
0
Нравится
0


