ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»
МЕТОДИЧЕСКОЕ ПОСОБИЕ
Для самостоятельной работы студентов
По дисциплине: МАТЕМАТИКА
Тема: «ПРОЦЕНТЫ И ВСЁ О НИХ»
Специальность: 34.02.01 Сестринское дело Курс: 2
(базовой подготовки)
Купино
2015
Рассмотрено на заседании предметной цикловой
Методической комиссии по общеобразовательным дисциплинам,
общему гуманитарному и социально-экономическому, математическому и
естественно-научному циклу
Протокол № _____ от «_____» _________20____г.
Председатель ПЦМК: _____________
Автор – составитель: преподаватель математики первой категории Тюменцева О.Н.
Купино
2015 г
Пояснительная записка к методическому пособию
Методическое пособие предназначено повторения теоретических и практических знаний по теме.
Цель пособия – повторить понятия: процент, отношения и пропорция, пропорциональность и подготовиться к занятию по теме «Основные математические методы решения прикладных задач в области профессиональной деятельности».
Данное пособие рекомендовано для студентов второго курса специальности 34.02.01 Сестринское дело. Пособие содержит определение и правило нахождения процентов, примеры задач с подробным решением, вопросы для самоконтроля, тест для самоконтроля и ключи к тесту.
Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.
Краткое содержание темы.
Процент – это сотая часть единицы. Запись 1% означает 0.01. Существует три основных типа задач на проценты:
Правило 1.Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь
Правило 2.Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.
Правило 3.Чтобы найти процентное отношение двух чисел А и В, надо отношение этих чисел умножить на 100%, то есть вычислить (а/в)*100%. Правило 4.Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби, а затем значение процентов разделить на эту дробь. Процентное содержание вещества в растворе (например, 15%), иногда называют %-м раствором, например, 15%-й раствор соли. Если концентрация вещества в соединении по массе составляет р%, то это означает, что масса этого вещества составляет р% от массы всего соединения. Если известно процентное содержание вещества, то его концентрация находится по формуле: К=р/100% к - концентрация вещества; р - процентное содержание вещества (в процентах). Чтобы увеличить положительное число а на р процентов, следует умножить число а на коэффициент увеличения к=(1+0,01р). Чтобы уменьшить положительное число а на р процентов, следует умножить число а на коэффициент уменьшения к= (1-0,01р). Правило 5.Чтобы найти, на сколько % положительное число у отличается от положительного числа а, следует вычислить, сколько % у составляет от а, а затем от полученного числа отнять а. Примеры:
1. Найдите 30 % от 60.
Решение:60·0,3 = 18.
2. Найдите число, если3 % числа его составляют 150.
Решение: х= 150: 0,03; х=5000.
3. Сколько процентов составляет 150 от 600?
Решение: 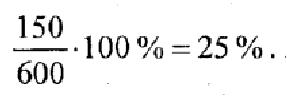
4. Увеличить число 60 на 20 %.
Решение:60 + 60·0,2 =72 или 60(1 + 0,2) = 72.
5. Число 72 уменьшили на 20 %.
Решение:72 — 72·0,2 = 57,6 или 72(1 —0,2) =57,6.
Процентное содержание. Процентный раствор.
6. Сколько кг соли в 10 кг соленой воды, если процентное содержание соли 15%.
Решение: 10 . 0,15 = 1,5 (кг) соли. Процентное содержание вещества в растворе (например, 15%), иногда называют %-м раствором, например, 15%-й раствор соли.
7. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?
Решение: Процентное содержание вещества в сплаве - это часть, которую составляет вес данного вещества от веса всего сплава.
1) 10 + 15 = 25 (кг) - сплав;
2) 10/25 . 100% = 40% - процентное содержание олова в сплаве;
3) 15/25 . 100% = 60% - процентное содержание цинка в сплаве; Концентрация. Если концентрация вещества в соединении по массе составляет р%, то это означает, что масса этого вещества составляет р% от массы всего соединения.
8. Концентрация серебра в сплаве 300 г составляет 87%.
Решение:300 . 0,87 = 261 (г). В этом примере концентрация вещества выражена в процентах. Отношения объема чистой компоненты в растворе ко всему объему смеси называется объемной концентрацией этой компоненты. Сумма концентраций всех компонент, составляющих смесь, равна 1. В этом случае концентрация - безразмерная величина. Если известно процентное содержание вещества, то его концентрация находится по формуле: к = р /100% к - концентрация вещества; р - процентное содержание вещества (в процентах).
9. Слиток сплава серебра с цинком весом в 3.5 кг содержал 76% серебра. Его сплавили с другим слитком и получили слиток весом в 10.5 кг, содержание серебра в котором было 84%. Сколько процентов серебра содержалось во втором слитке?
Решение:
1) 3.5-0.76 = 2.66 (кг) серебра в первом слитке.
2) 10.5-0.84 = 8.82 (кг) серебра в 10.5 кг сплава.
3) 8.82 - 2.66 = 6.16 (кг) серебра во втором слитке.
4) 10.5 - 3.5 = 7 (кг) вес второго слитка.
5) 6.16: 7 = 0.88 = 88% серебра содержалось во втором слитке.
Вопросы для самоподготовки:
1. Как найти данное число процентов от числа.
2. Как найти, сколько процентов одно число составляет от другого
3. Как найти процентное отношение двух чисел А и В
4. Как найти число по данным его процентам
5. Как найти концентрацию раствора
6. Что следует делать, чтобы увеличить положительное число а на р процентов.
Тест для самоконтроля:
1. Из 100 куколок при благоприятных условиях на свет появляются 70 % бабочек. Сколько бабочек появится из 2100 куколок?
а) 1470 бабочек
б) 3 бабочек
в) 14700 бабочек
2. Содержание эфирного масла в лепестках розы составляет в среднем 4 %. Сколько эфирного масла можно получить из лепестков розы?
а) 3 г
б) 4 г
в) 0,1 г
3. Средний рост девочек того же возраста, что и Наташа, равен 150 см. Рост Наташи на 8 % выше среднего. Какой рост у Наташи?
а) 150 см
б) 158 см
в) 162 см
4. В цветочном магазине цена непроданной розы каждый день снижается на 15 %. Сколько будет стоить роза на третий день, если в первый день ее продали по 80 рублей?
а) 68 рублей
б) 57 рублей 8 копеек
в) 80 рублей
5. Найти число, если 15% его равны 30.
а) 200
б) 150
в) 100
6. Сколько кг соли в 10 кг соленой воды, если процентное содержание соли 15%.
а) 1,5
б) 1,2
в) 150
7. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?
а) 40% - содержание олова в сплаве, 60% - содержание цинка в сплаве.
б) 25% - содержание олова в сплаве, 60% - содержание цинка в сплаве.
в) 40% - содержание олова в сплаве, 25% - содержание цинка в сплаве.
8. К 120 г раствора, содержащего 80% соли, добавили 480 г раствора, содержащего 20 % той же соли. Сколько процентов соли содержится в получившемся растворе?
а) 96%
б) 32%
в) 52%
9. Концентрация серебра в сплаве 300 г составляет 87%. Сколько чистого серебра в сплаве?
а) 344
б) 26100
в) 261
10. Матроскин продает молоко через магазин и хочет получать за него 25 рублей за литр. Магазин удерживает 20% стоимости проданного товара. По какой цене будет продаваться молоко в магазине?
а) 30 рублей
б) 33 рубля
в) 31 рубль 25 копеек
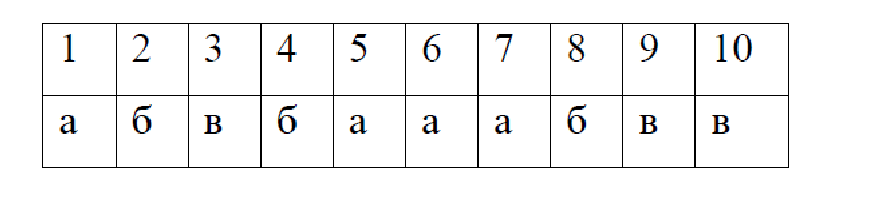
Ключ для самопроверки теста:


 Получите свидетельство
Получите свидетельство Вход
Вход



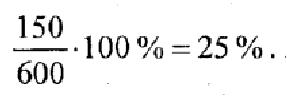










 Методическое пособие для самостоятельной работы студентов по теме "Проценты и все о них" (66 КB)
Методическое пособие для самостоятельной работы студентов по теме "Проценты и все о них" (66 КB)
 0
0 529
529 17
17 Нравится
0
Нравится
0


