Основные понятия систем счисления

СИСТЕМЫ СЧИСЛЕНИЯ

Основные понятия

Подготовил преподаватель Бурдин А.Б.

Компьютер имеет дело с различными видами информации, которая, как правило, кодируется числами. Компьютер обрабатывает числовую информацию не только при выполнении расчетов, но и при представлении компьютерной графики, текста и т.д.

Представление различных видов информации определяет не только способ записи данных, но и набор допустимых операций над ними. В связи с этим встает вопрос о выборе оптимального представления чисел в компьютере.

Числа могут быть представлены в различных системах счисления.

Число обладает двумя свойствами:

• Значением ;
• Формой представления .

Значение числа – сравнение с другими числами («больше», «меньше», «равно»). Числа можно расположить в определенном порядке на числовой оси.

Форма представления числа определяет порядок его записи с помощью предназначенных для этого знаков.

Значение числа остается неизменным при любой форме его представления. Это означает, что число с одним и тем же значением может быть записано по-разному.

Например, числу 12 в десятичной системе соответствует запись XII римскими цифрами . Способ представления числа определяется системой счисления.

Система счисления – это правило записи чисел с помощью заданного набора специальных знаков – цифр.

Люди создали различные способы записи чисел, а следовательно, и различные системы счисления. Но все их можно разделить на позиционные и непозиционные .

Непозиционные – это системы счисления, в которых «весовое» значение цифры не зависит от ее позиции в записи числа.

Из непозиционных систем счисления наиболее распространенной или известной можно считать римскую систему счисления. В ней числа обозначаются латинскими буквами: 1 – I; 5 – V; 10 – X; 50 – L; 100 – C, 500 – D.

Все другие числа строятся из базовых в соответствии со следующими правилами:

• Если цифра меньшего значения стоит справа от большей цифры, то их значение суммируются, если слева – то меньшее вычитается из большего;
• Цифры I, X, C, могут следовать подряд не более трех раз каждая;
• Цифры V, L, D могут использоваться в записи числа не более одного раза.

Например,

XXIV = 10 + 10+ 5 – 1 = 24

Запись чисел в такой системе громоздка и неудобна. В этой системе трудно выполнять простые арифметические операции.

Отсутствие нуля и знаков для чисел больше М (1000) не позволяет записать римскими цифрами любое число.

Такие системы счисления называют аддитивными , т.к. значение числа определяется посредством операций сложения и вычитания базисных цифр.

В настоящее время для представления чисел применяются в основном позиционные системы счисления .

Позиционные – это системы счисления, в которых значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.

Любая позиционная система счисления характеризуется основанием .

Основание позиционной с/с – это количество различных цифр, используемых для записи числа.

Если для записи числа используются две цифры, то с/с – двоичная, три – троичная.

В десятичной с/с используется 10 цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

В этом ряду цифры упорядочены по своим значениям. Например, цифра 7 имеет большее значение, чем цифра 5. но весовое значение цифры определяется еще и ее местоположением в числе – позицией .

Позиции цифр, отсчитываемые от какой-то начальной точки, называются разрядами .

В десятичной с/с цифры 1-го разряда – единицы, 2-го разряда – десятки, 3-го – сотни:

325 = 3 × 100 + 2 × 10 + 5 × 1

Историческое развитие вычислительной техники сложилось таким образом, что цифровые компьютеры строятся на базе двоичных цифровых устройств.

ОСНОВА-НИЕ

НАЗВАНИЕ

2

АЛФАВИТ

двоичная

8

восьмеричная

0 1

10

0 1 2 3 4 5 6 7

десятеричная

16

шестнадцатеричная

0 1 2 3 4 5 6 7 8 9

0 1 2 3 4 5 6 7 8 9 А B C D E F

Основной системой счисления, применяемой в компьютере, является двоичная система, т.к. она имеет ряд преимуществ :

• Для её реализации нужны технические устройства с двумя устойчивыми состояниями ;
• Представление информации с помощью только двух состояний надежно и помехоустойчиво ;
• Возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
• Двоичная арифметика проще десятичной .

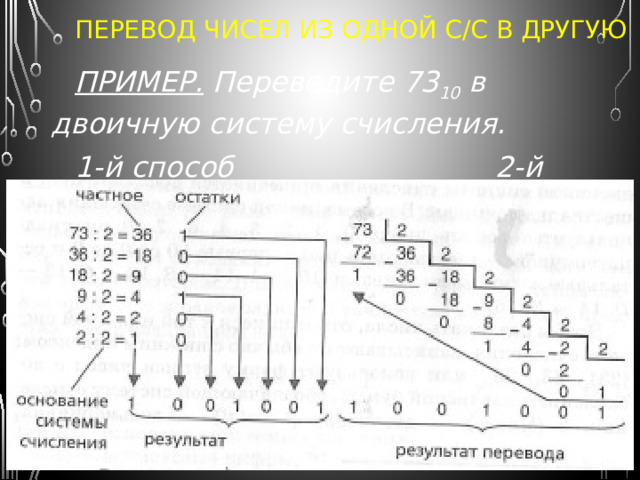
ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ С/С В ДРУГУЮ

Перевод целых чисел из десятичной с/с в недесятичную осуществляется последовательным делением десятичного числа на основание той системы, в которую переводится, до тех пор, пока не получится частное меньше этого основания.

Число в новой системе записывается в виде полученных остатков деления, начиная с последнего частного, которое меньше основания.

ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ С/С В ДРУГУЮ

ПРИМЕР. Переведите 73 10 в двоичную систему счисления.

1-й способ 2-й способ

ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ С/С В ДРУГУЮ

Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы, из которой переводится число. Затем подсчитывается общая сумма.

ПРИМЕР. 10011 2

10011 2 =

4 3 2 1 0

1×2 4 +0×2 3 +0×2 2 +1×2 1 +1×2 0

16+0+0+2+1 = 19 10

ДЗ

Перевести из десятичной с/с в двоичную числа: 12, 45, 63

Перевести из двоичной с/с в десятичную числа: 101110, 10101, 11100

Использованная литература:

Л-5, стр. 98-102

Фиошин М.Е. Информатика и ИКТ.10-11 кл.