4
Практическая РАБОТА по Теме: «Системы счисления. Перевод чисел из одной системы счисления в другую»
Цель работы – приобретение навыков выполнения операций в различных системах счисления.
Основные понятия систем счисления
Система счисления — это совокупность правил и приемов записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления.
Основание системы записывается в справа числа в нижнем индексе: 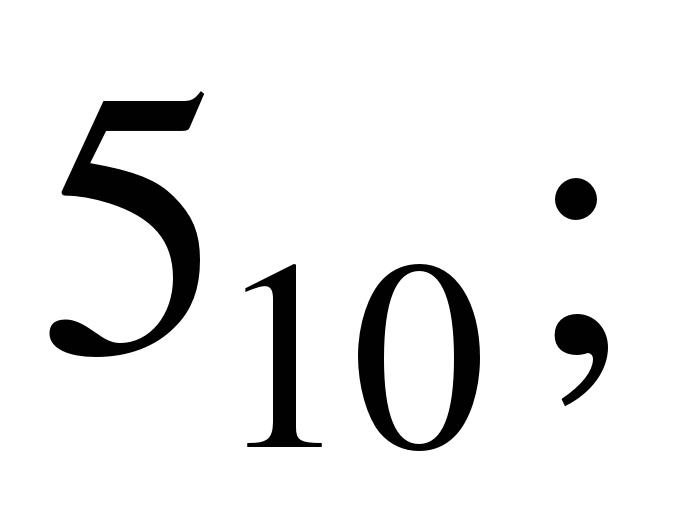
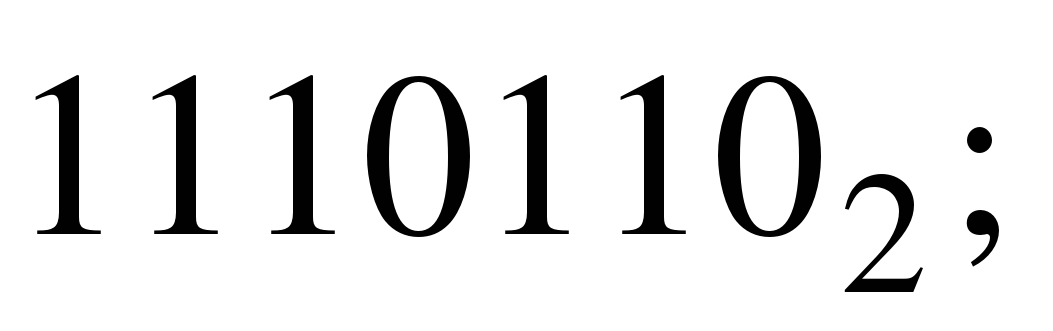
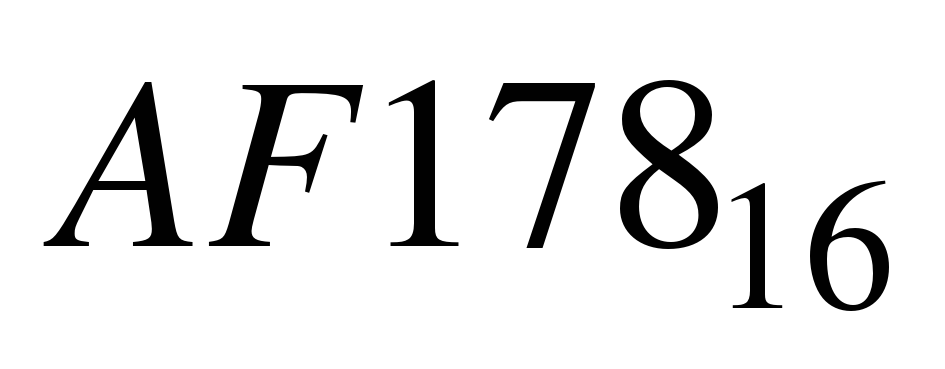 .
.
Различают два типа систем счисления:
позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.
Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.д. Примером позиционной системы счисления является десятичная система, используемая повседневно.
Любое целое число в позиционной системе можно записать в форме многочлена:
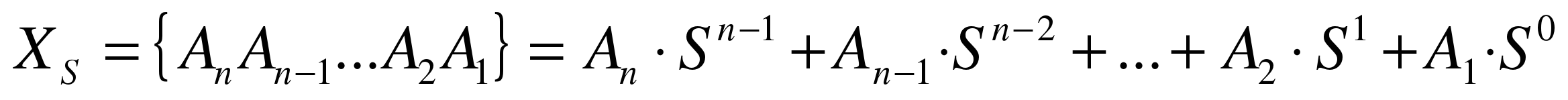 ,
,
где  — основание системы счисления;
— основание системы счисления;
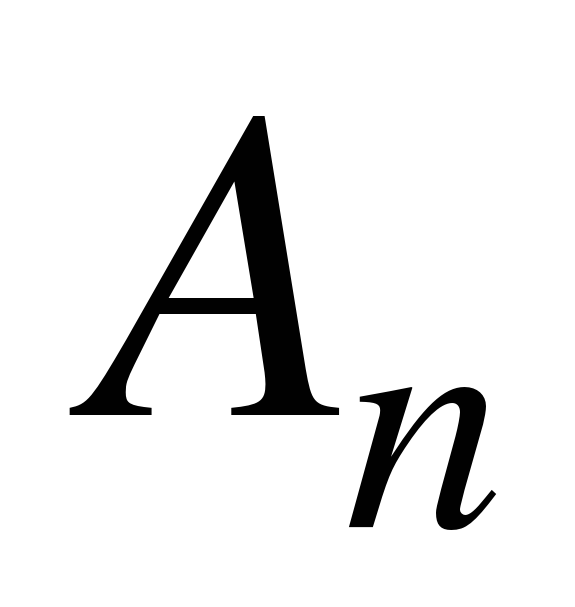 — цифры числа, записанного в данной системе счисления;
— цифры числа, записанного в данной системе счисления;
n — количество разрядов числа.
Пример. Число 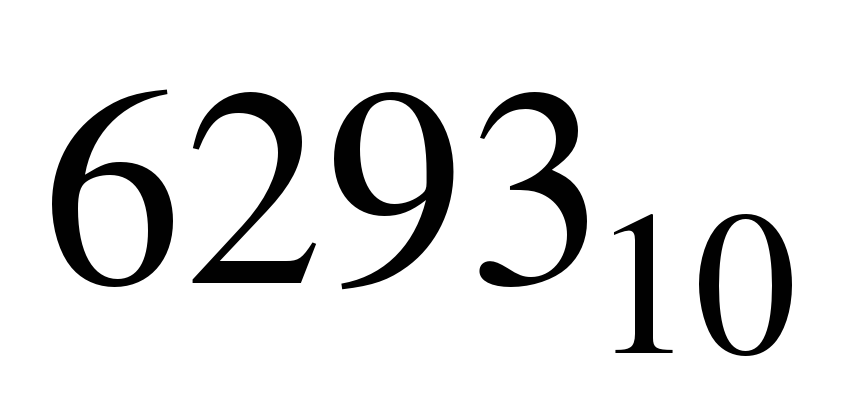 запишется в форме многочлена следующим образом:
запишется в форме многочлена следующим образом:
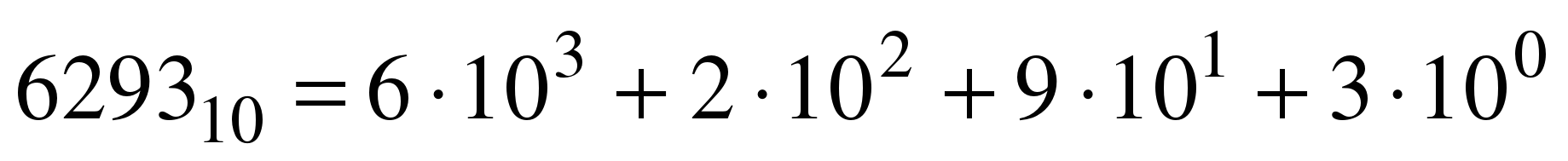
В вычислительных машинах используется двоичная система счисления, её основание — число 2. Для записи чисел в этой системе используют только две цифры — 0 и 1.
Таблица 1. Соответствие чисел, записанных в различных системах счисления
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| 1 | 001 | 1 | 1 |
| 2 | 010 | 2 | 2 |
| 3 | 011 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
Правила перевода чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
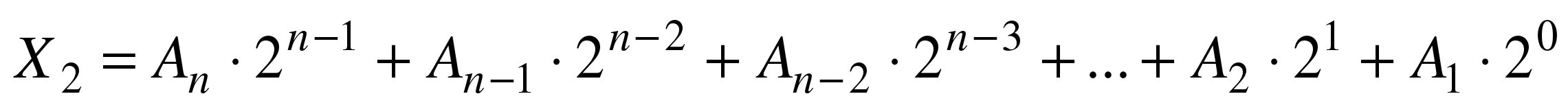
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 2. Степени числа 2
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 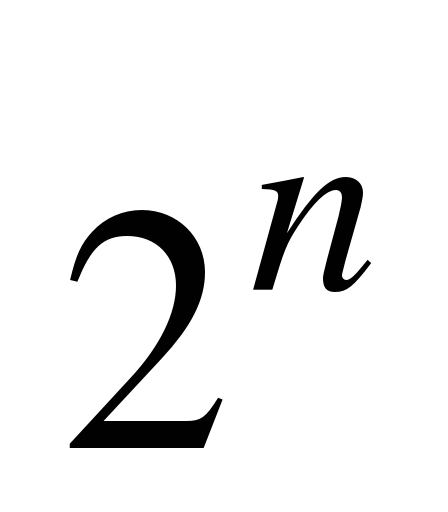
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
Пример. Число 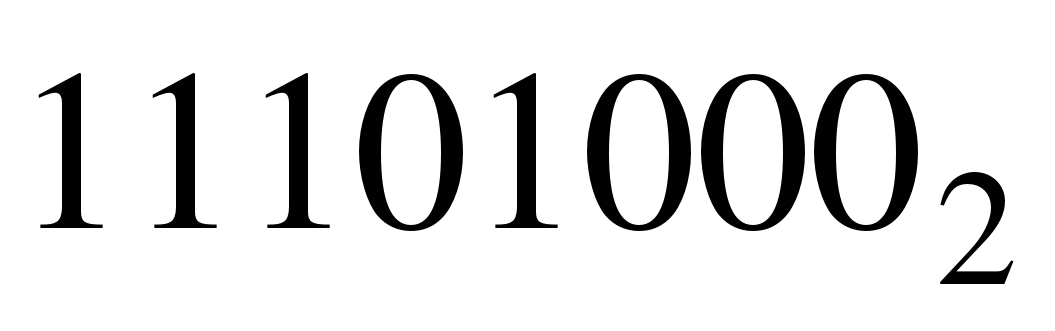 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
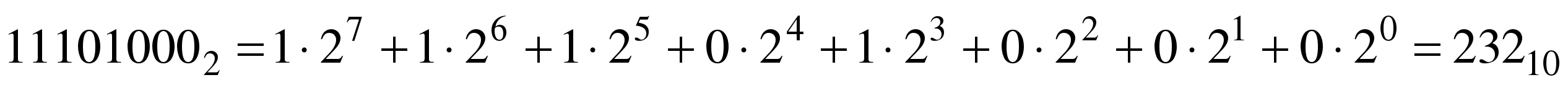
Переведите самостоятельно: 110111012; 1100010112.
Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
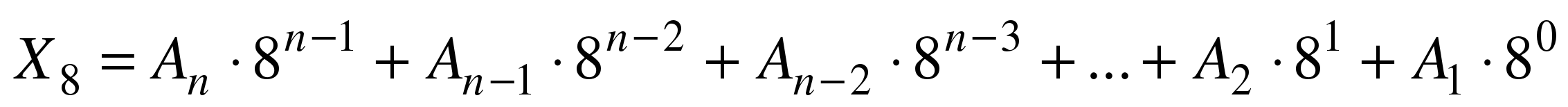
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 3.4. Степени числа 8
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 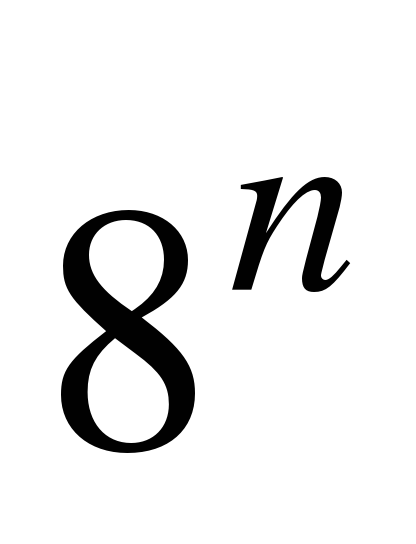
| 1 | 8 | 64 | 512 | 4096 | 32768 | 262144 |
Пример. Число 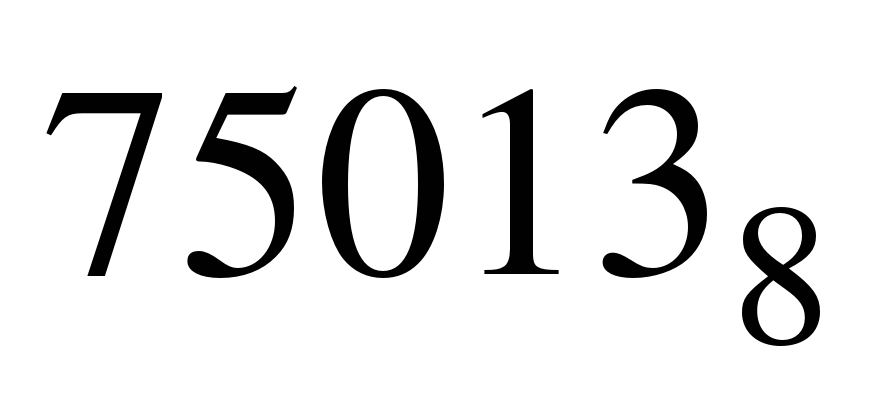 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
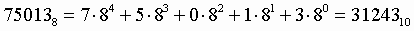
Переведите самостоятельно: 358 ; 658 ; 2158 ; 3278
Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
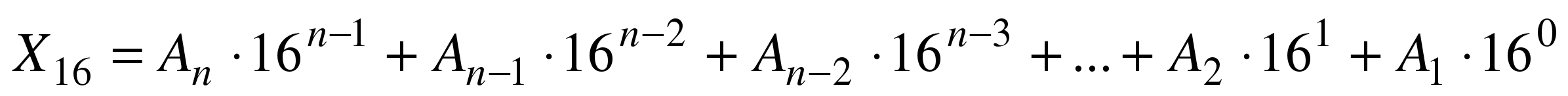
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 3. Степени числа 16
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 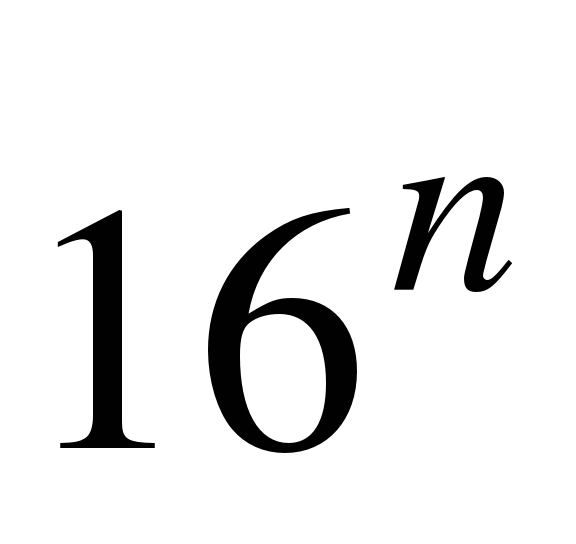
| 1 | 16 | 256 | 4096 | 65536 | 1048576 | 16777216 |
Пример. Число  перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
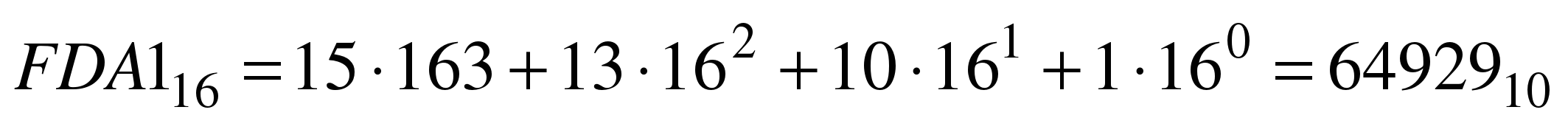
Переведите самостоятельно: D816 ; 1AE16 ; E5716 ; 8E516
Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число 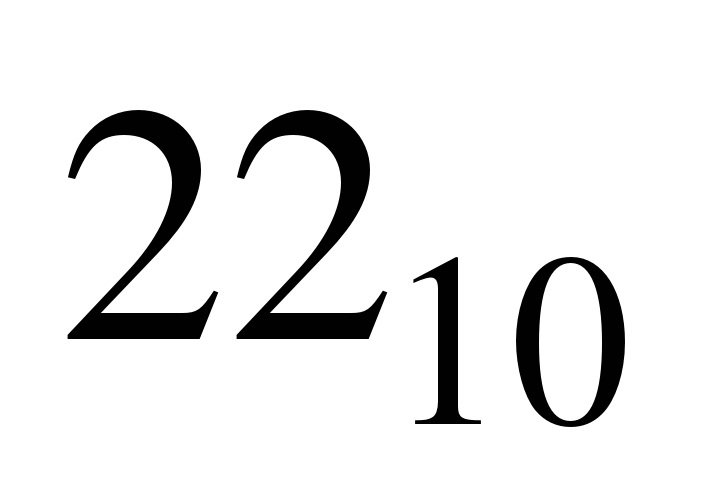 перевести в двоичную систему счисления.
перевести в двоичную систему счисления.
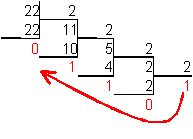
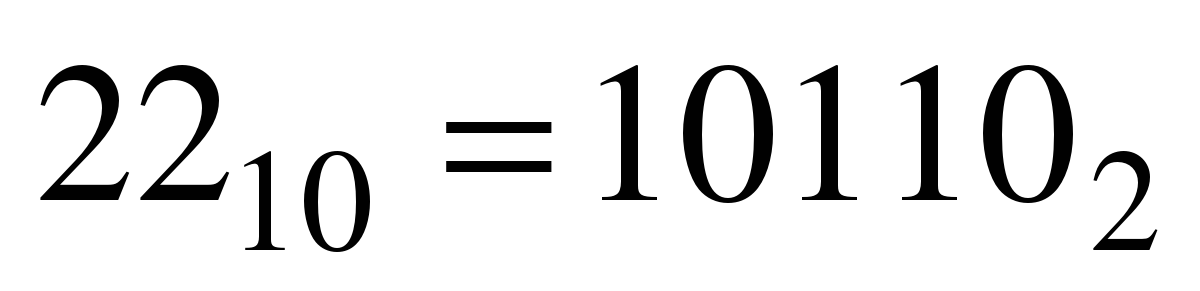
Переведите самостоятельно: 165; 541; 600; 720
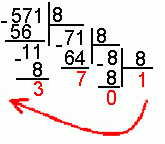
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число 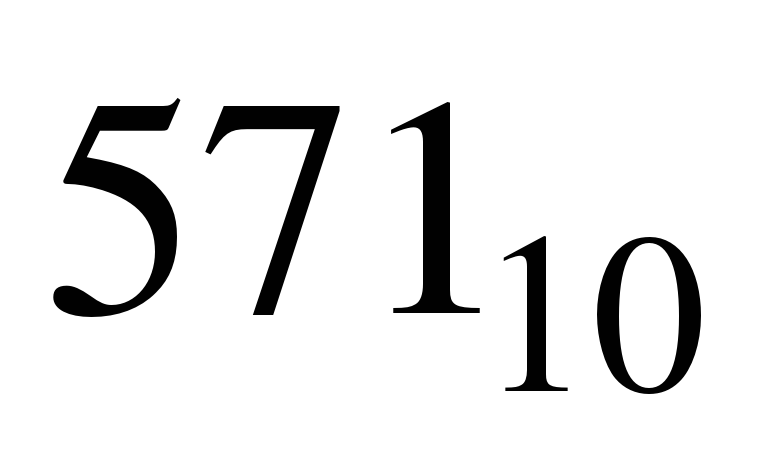 перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.

Переведите самостоятельно: 69; 73; 113; 203
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в шестнадцатеричную систему счисления.

Переведите самостоятельно: 113; 203; 351; 641
Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число перевести в восьмеричную систему счисления.

Переведите самостоятельно: 1001011102; 1000001112
Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число перевести в шестнадцатеричную систему счисления.

Переведите самостоятельно: 1110010112; 10110010112
Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Пример. Число перевести в двоичную систему счисления.

Переведите самостоятельно: 648; 4538; 738; 513
Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример. Число перевести в двоичную систему счисления.

Переведите самостоятельно: ABC16; F0B16
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 1. Число перевести в восьмеричную систему счисления.

Переведите самостоятельно: 2EA16; FCE16
Пример 2. Число перевести в шестнадцатеричную систему счисления.
Переведите самостоятельно: 7638; 7658
![]()
![]()
![]() .
.

 Получите свидетельство
Получите свидетельство Вход
Вход














 Практическая работа по информатике "Системы счисления" (0.13 MB)
Практическая работа по информатике "Системы счисления" (0.13 MB)
 0
0 8148
8148 1324
1324 Нравится
0
Нравится
0


