Научный проект "Системы счисления"

Проект на тему «Системы счисления(СС)»

Руководители

Морозова Л. А.

учитель математики, Венкова В. С. учитель информатики

МБОУ «СОШ № 51» г. Курска

Автор Венков К. С.

Ученик 5 «В» класса

МБОУ «СОШ № 51» г. Курска

М. В. Ломоносов

Вопросы

Содержание

• теоретический материал
• практическое применение, эксперимент

Глава I ( подбор теоретического материала)

Что такое система счисления?

Система счисления — это правила записи чисел с помощью специальных знаков — цифр , а также соответствующие правила выполнения операций с этими числами.

Счёт на пальцах:

Унарная (лат. unus – один) – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …)

• только натуральные числа
• запись больших чисел – длинная (1 000 000?)

Египетская система счисления

лотос

черта

– 1

– 10

– 100

– 1000

– 10000

– 100000

– 1000000

палец

хомут

человек

лягушка

верёвка

=1235

= ?

2016 = ?

Непозиционные системы счисления

Непозиционная система счисления: значение цифры не зависит от её места в записи числа.

• египетская
• римская
• славянская
• унарная
• и другие…

« Пираты XX века»

Римская система счисления

Правила:

• (обычно) не ставят больше трех одинаковых цифр подряд если младшая цифра (только одна !) стоит слева от старшей, она вычитается из суммы ( частично непозиционная!)
• (обычно) не ставят больше трех одинаковых цифр подряд
• если младшая цифра (только одна !) стоит слева от старшей, она вычитается из суммы ( частично непозиционная!)

Примеры:

MDC X L I V =

– 10

+ 5

+ 50

– 1

+ 100

+ 500

1000

= 1644

2389 = 2000 + 300 + 80 + 9

M M

CCC

LXXX

IX

2389 = M M C C C L X X X I X

Римская система счисления

• только натуральные числа ( дробные ? отрицательные ?)
• для записи больших чисел нужно вводить новые цифры
• сложно выполнять вычисления

Смешанные системы счисления

1 коп., 5 коп., 10 коп., 50 коп., 1 руб., 2 руб., 5 руб., 10 руб., 50 руб., 100 руб., 500 руб., 1000 руб. и 5000 руб.

313121200000

Позиционные системы счисления

Позиционная система: значение цифры определяется ее позицией в записи числа.

Алфавит системы счисления — это используемый в ней набор цифр.

Основание системы счисления — это количество цифр в алфавите ( мощность алфавита ).

Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.

Формы записи чисел

развёрнутая форма записи числа

тысячи сотни десятки единицы

разряды

3 2 1 0

= 6 ·10 3 + 3 ·10 2 + 7·10 1 + 5·10 0

6 3 7 5

5

70

6000

300

Схема Горнера:

6 3 7 5 = ((6  10 + 3)  10 + 7)  10 + 5

• для вычислений не нужно использовать возведение в степень
• удобна при вводе чисел с клавиатуры, начиная с первой

Перевод в десятичную систему

Через развёрнутую запись:

=1

разряды : 3 2 1 0

1234 5 = 1  5 3 + 2  5 2 + 3  5 1 + 4  5 0 = 194

основание системы счисления

разряды : 3 2 1 0

a 3 a 2 a 1 a 0 = a 3  p 3 + a 2  p 2 + a 1  p 1 + a 0  p 0

Через схему Горнера:

1234 5 = (( 1  5 + 2 )  5 + 3 )  5 + 4 = 194

a 3 a 2 a 1 a 0 = (( a 3  p + a 2 )  p + a 1 )  p + a 0

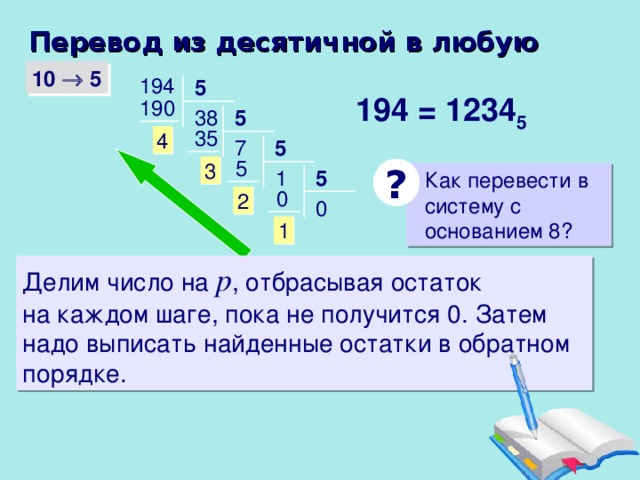
Перевод из десятичной в любую

10  5

194

5

194 = 1234 5

190

38

5

35

4

5

7

5

3

?

5

1

Как перевести в систему с основанием 8?

0

2

0

1

Делим число на p , отбрасывая остаток

на каждом шаге, пока не получится 0. Затем надо выписать найденные остатки в обратном порядке.

Глава I I ( практическое применение)

В опросе принимали участие

ученики 5-х классов

МБОУ «СОШ № 51»

ВСЕГО: 60 человек

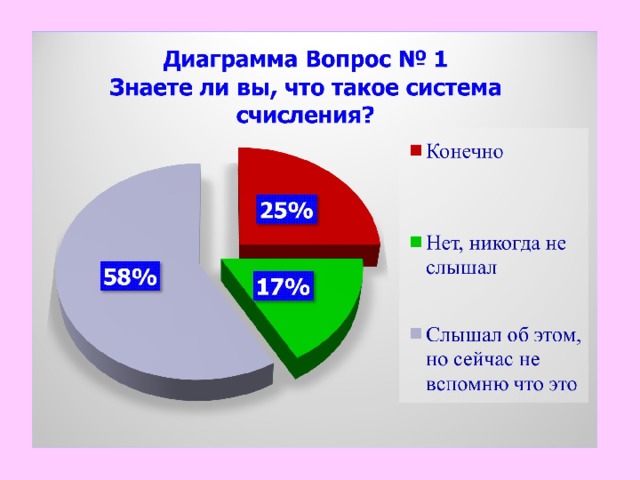
Вопрос № 1 Знаете ли вы, что такое система счисления?

• Конечно
• Нет, никогда не слышал
• Слышал об этом, но сейчас не вспомню что это

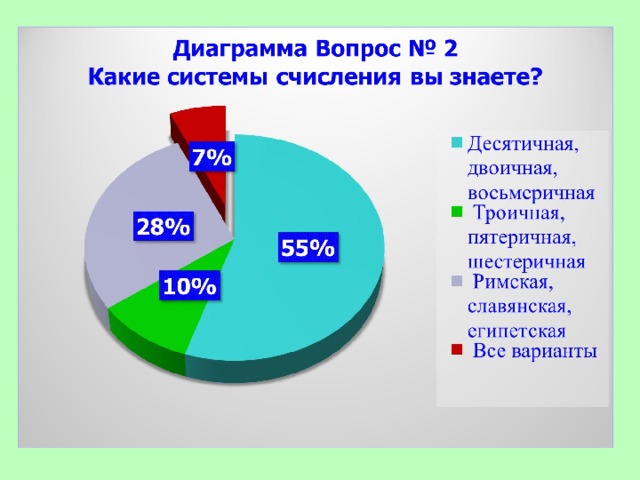
Вопрос № 2 Какие системы счисления вы знаете?

• Десятичная, двоичная, восьмеричная
• Троичная, пятеричная, шестеричная
• Римская, славянская, египетская
• Все варианты

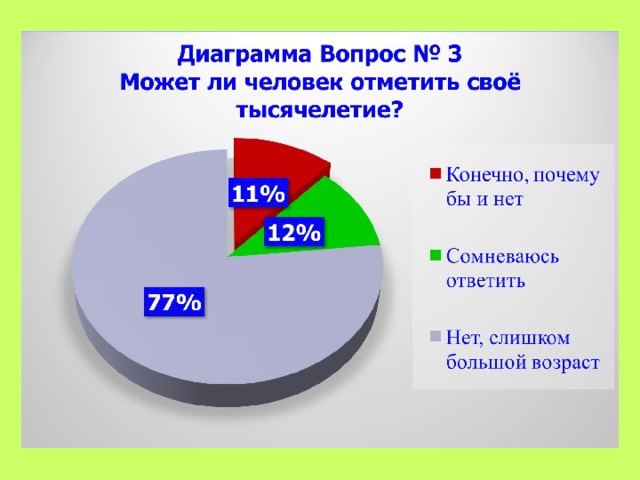
Вопрос № 3 Может ли человек отметить своё тысячелетие?

• Конечно, почему бы и нет
• Сомневаюсь ответить
• Нет, слишком большой возраст

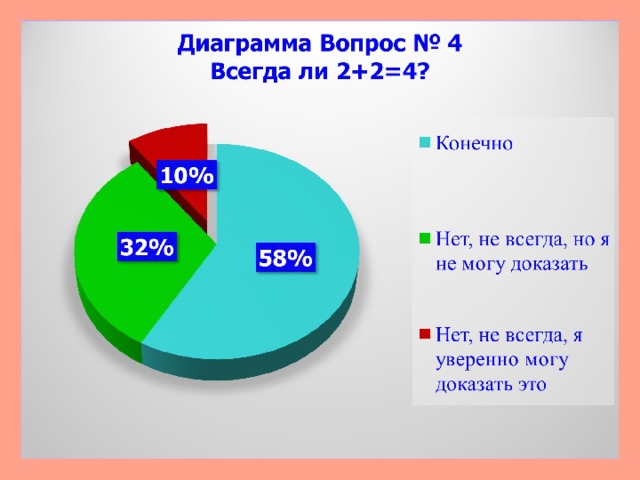
Вопрос № 4 Всегда ли 2+2=4?

• Конечно
• Нет, не всегда, но я не могу доказать
• Нет, не всегда, я уверенно могу доказать это

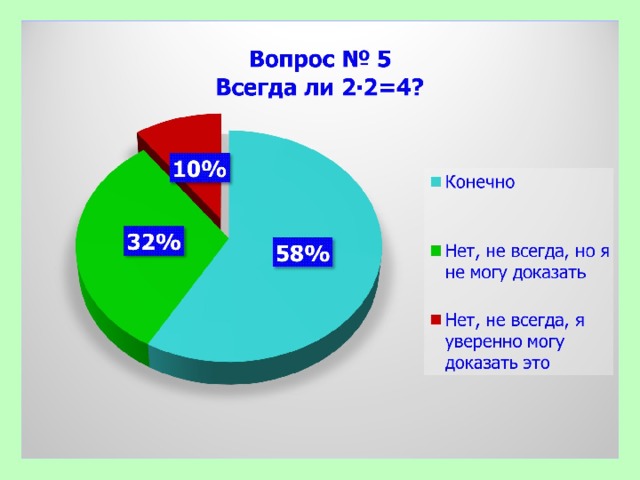
• Конечно
• Нет, не всегда, но я не могу доказать
• Нет, не всегда, я уверенно могу доказать это

Результаты проведенного опроса

учащихся 5-х классов

МБОУ «СОШ № 51»

Вопросы

В двоичной СС - это число «2»

М. В. Ломоносов