Прикладной курс «Модуль числа».
Из опыта работы учителя математики школы-гимназии № 22 г. Астаны
Цильсдорф Г.Б.
|
Краткое описание курса: Понятие модуля является одной из важнейших характеристик числа в области действительных чисел. Программой школьного курса математики не предусмотрены обобщение и систематизация знаний о модулях, их свойствах, полученных учащимися за весь период обучения. Это и позволит сделать прикладной курс «Абсолютная величина (модуль)». Курс рассчитан на учащихся 9-11 классов общеобразовательных школ, проявляющих интерес к изучению математики. Пояснительная записка Понятие «модуль» широко применяется не только в различных разделах школьного курса математики, но и в курсах высшей математики, физики и технических наук, изучаемых в вузах. Например, в теории приближенных вычислений используются понятия абсолютной и относительной погрешностей приближенного числа. В механике и геометрии изучаются понятия вектора и его длины (модуля вектора). В математическом анализе понятие абсолютной величины числа содержится в определениях таких основных понятий, как предел, ограниченная функция и др. Задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах, в тестовых заданиях ЕНТ. Курс позволит школьникам систематизировать, расширить и укрепить знания, связанные с абсолютной величиной, подготовиться для дальнейшего изучения тем, использующих это понятие, научиться решать разнообразные задачи различной сложности, способствует выработке и закреплению навыков работы на компьютере. Учителю курс поможет наиболее качественно подготовить учащихся к математическим олимпиадам, сдаче ЕНТ. Программа прикладного курса предполагает знакомство с теорией и практикой рассматриваемых вопросов и рассчитана на 34 часа. Содержание курса состоит из восьми разделов, включая введение и итоговое занятие. Учитель, в зависимости от уровня подготовки учащихся, уровня сложности изучаемого материала и восприятия его школьниками, может взять для изучения не все темы, увеличив при этом количество часов на изучение других. Учитель также может изменить уровень сложности представленного материала. Результатом освоения программы курса является представление школьниками творческих индивидуальных и групповых работ на итоговом занятии. Цели курса: обобщение и систематизация, расширение и углубление знаний по теме «Абсолютная величина»; обретение практических навыков выполнения заданий с модулем; повышение уровня математической подготовки школьников. Задачи курса: вооружить учащихся системой знаний по теме «Абсолютная величина»; сформировать навыки применения данных знаний при решении разнообразных задач различной сложности; подготовить учащихся к ЕНТ; сформировать навыки самостоятельной работы, работы в малых группах; сформировать умения и навыки исследовательской работы; способствовать развитию алгоритмического мышления учащихся; способствовать формированию познавательного интереса к математике. Требования к уровню усвоения учебного материала В результате изучения программы элективного курса «Абсолютная величина (модуль)» учащиеся получают возможность знать и понимать: определение абсолютной величины действительного числа; основные операции и свойства абсолютной величины; правила построения графиков функций, содержащих знак абсолютной величины; алгоритмы решения уравнений, неравенств, систем уравнений и неравенств, содержащих переменную под знаком модуля. Уметь: применять определение, свойства абсолютной величины действительного числа к решению конкретных задач; читать и строить графики функций, аналитическое выражение которых содержит знак абсолютной величины; решать уравнения, неравенства, системы уравнений и неравенств, содержащих переменную под знаком модуля. Содержание курса (1 ч в неделю, всего 34 ч) 1. Введение (1 ч). Цели и задачи элективного курса. Вопросы, рассматриваемые в курсе и его структура. Знакомство с литературой, темами творческих работ. 2. Абсолютная величина действительного числа а (4 ч). Абсолютная величина действительного числа а. Модули противоположных чисел. Геометрическая интерпретация понятия модуля а. Модуль суммы и модуль разности конечного числа действительных чисел. Модуль разности модулей двух чисел. Модуль произведения и модуль частного. Операции над абсолютными величинами. Упрощение выражений, содержащих переменную под знаком модуля. Применение свойств модуля при решении олимпиадных задач. 3. Графики функций, аналитическое выражение которых содержит знак абсолютной величины (8 ч). . Правила и алгоритмы построения графиков функций, аналитическое выражение которых содержит знак модуля. Графики уравнений
Графики некоторых простейших функций, заданных явно и неявно, аналитическое выражение которых содержит знак модуля. Графики функций, аналитическое выражение которых содержит знак абсолютной величины в олимпиадных заданиях. 4. Уравнения, содержащие абсолютные величины (13 ч). Основные методы решения уравнений с модулем. Раскрытие модуля по определению, переход от исходного уравнения к равносильной системе, возведение в квадрат обеих частей уравнения, метод интервалов, графический метод, использование свойств абсолютной величины. Уравнения вида
Метод замены переменных при решении уравнений, содержащих абсолютные величины. Метод интервалов при решении уравнений, содержащих абсолютные величины. Уравнения вид
Способ последовательного раскрытия модуля при решении уравнений, содержащих «модуль в модуле». Графическое решение уравнений, содержащих абсолютные величины. Использование свойств абсолютной величины при решении уравнений. Уравнения с параметрами, содержащие абсолютные величины. Защита решенных олимпиадных заданий. 5. Неравенства, содержащие абсолютные величины (8 ч). Неравенства с одним неизвестным. Основные методы решения неравенств с модулем. Неравенства вида
Неравенства вида
Метод интервалов при решении неравенств, содержащих знак модуля. Неравенства с параметрами, содержащие абсолютные величины. Неравенства с двумя переменными. Учебно-тематический план
Темы творческих работ. Применение модуля в механике и векторной алгебре. Модуль в определении предела. Погрешности. Проект памятки правил и алгоритмов построения графиков функций, аналитическое выражение которых содержит знак модуля. Проект опорных сигналов по способам решения уравнений и неравенств с модулем. Простейшие функции, заданные явно и неявно, аналитическое выражение которых содержит знак модуля, и их графики. Литература Башмаков М.И. Уравнения и неравенства. – М.: ВЗМШ при МГУ, 1983. Виленкин Н.Я. и др. Алгебра и математический анализ. 11 кл. – М.: Просвещение, 1993. Галицкий М.Л. и др. Сборник задач по алгебре 8 – 9 кл. – М.: Просвещение, 1995. Олехник С.Н. и др. Уравнения и неравенства. Нестандартные методы решения. 10 – 11 кл. – М.: Дрофа, 1995. Петраков И.С. Математика для любознательных. М. Просвещение 2000г. Шарыгин И.Ф. Факультативный курс по математике 10 – 11 кл – М.: Просвещение, 89.
|

 Получите свидетельство
Получите свидетельство Вход
Вход


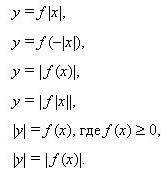
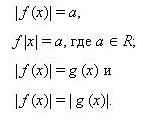
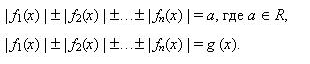
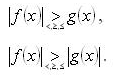









 "Модуль числа" прикладной курс по математике. (36.63 KB)
"Модуль числа" прикладной курс по математике. (36.63 KB)
 0
0 846
846 26
26 Нравится
0
Нравится
0


