XIII городская научно-практическая конференция
учащихся 5-8 классов по математике, физике, информатике
«Обыкновенное чудо»
МАОУ «Физико-математическая школа № 56» г. Улан-Удэ
Секция: математика
Тема: «Множества, операции над ними, их свойства и применение при решении задач»
Автор: Агафонов Даниил Иванович
учащийся 6 е класса
Руководитель: Шмакова Галина Николаевна,
учитель математики
высшей квалификационной категории
МАОУ «ФМШ №56»
Улан-Удэ
2025
Оглавление
1. Введение…………………………………………………………… 3 стр.
1.1. Выбор темы исследования…………………………………... 3 стр.
1.2. Цель исследования……………………………………………. 3 стр.
1.3. Задачи исследования………………………………………….. 3 стр.
1.4. Гипотеза исследования………………………………………. 3 стр.
1.5. Актуализация знаний………………………………………… 4 стр.
1.6. Постановка проблемы исследования………………………. 4 стр.
2. Основная часть…………………………………………………….. 4 стр.
2.1. Теоретический материал……………………………………… 4 стр.
2.1.1 Способы выражения множеств…………………………... 5 стр.
2.1.2 Визуализация множеств…………………………………… 5 стр.
2.2. Практическая часть………………………………………… 6 стр.
2.2.1. Опрос……………………………………………………… 6 стр.
2.2.2 Арифметические действия и операции над множествами 7 стр.
3. Вывод………………………………………………………………….9 стр.
3.1. Доказательство гипотезы…………………………………… 9 стр.
3.2. Продукт проекта………………………………………………. 10 стр.
4. Заключение…………………………………………………………... 10 стр.
Литература……………………………………………………………… 11 стр.
Приложения №1 Сборник задач……….…………………………….. 12 стр.
Приложения №2 «Это интересно!»………………………………… 14 стр.
1. Введение
1.1.Выбор темы исследования.
Каждый человек встречается с множествами, иногда сам того не зная. Множество простых, составных чисел, остроугольных треугольников, объемных фигур. Эти понятные и простые множества всегда с нами.
Но как много знают о множествах ученики моего класса? Считают ли они эту тему ненужной или скучной? Знают ли они, где множества находят себе применение? На эти и другие вопросы я хочу ответить своей работой.
1.2. Цель исследования.
Выяснить что же такое множества, изучить специальные знаки, используемые в этой области.
Определить степень знаний учеников моего класса по этой теме, их отношение к ней.
1.3.Задачи исследования.
1.Проанализировать литературу и интернет-ресурсы по данной теме
2. Выяснить, какие действия над множествами существуют
3. Рассмотреть применение теории множеств при решении задачи
4. Научиться составлять задачи с множествами
5.Провести опрос одноклассников, доказать гипотезу
Объект. Алгебра
Предмет. Множества
1.4.Гипотеза исследования.
Ученики моего класса мало знают о множествах, их применении и решении задач с ними. После ознакомления с теорией множества и операциями над ними, они поймут, что:
решение задач на множества основывается на логике;
операции над множествами не отличаются от обычных математических операций.
Методы исследования:
Поисковый.
Исследовательский.
Анализ интернет-ресурсов, литературы, знаний учеников моего класса, опрос, анкетирование.
Создание сборника задач.
1.5. Актуализация знаний.
Множество – совокупность объектов, объединенных по какому-нибудь признаку.
Множества обозначают большими буквами латинского алфавита: А, В, С, D и т. д.
Обозначения некоторых числовых множеств:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I - множество иррациональных чисел;
R – множество действительных чисел.
Виды множеств:
Равные множества
{А, Е, Ё, И, О, У, Ы, Э, Ю, Я} = {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}
Конечные множества
А = {2; 3; 5; 7; 11; 13};
Бесконечные множества
{1; 4; 9; 16; 25; …}; {10; 20; 30; 40; 50; …};
Пустое множество (обозначается символом Ø);
5.Счетные/Несчетные.
1.6. Постановка проблемы исследования.
Основополагающий и проблемные вопросы:
Как хорошо знают ученики моего класса тему «множества»?
Проблемный вопрос:
Как умеют решать задачи при помощи множеств и операций над ними? Учебные вопросы:
Знают они стандартные методы решения или решают на основе логики?
Отличаются ли операции над множествами от обычных математических? Если да, то насколько?
С чем связан выбор метода решения задач?
2.Основная часть
2. 1. Теоретический материал
Рассмотрим на более привычным для нас множествам – числовым. И начнем с натуральных чисел. Очевидно, что множество натуральных чисел (ℕ) счетное просто по определению. Если мы добавим к натуральным числам ноль и отрицательные числа, мы получим множество целых чисел. Счетное ли это множество? Если объединить два счетных множества, в результате также будет счетным множеством. От добавления 0 множество не потеряет свойства быть счетным.
Далее рассмотрим рациональные числа. Это множество чисел, представимых в виде m/n, где m – целое число, а n – натуральное:
Таким образом, рациональные числа представляют собой счетное число счетных множеств и при объединении также станут счетным множеством.
2.1.1. Способы описания множеств:
Перечисление (характерно для конечных множеств)
Характеристическое свойство (общее для конечных и бесконечных. Свойство общее для всех элементов множества, но которого нет у
элементов, не входящих в множество.)
Например: А{x|x 15,} (бесконечное множество чисел, больших 15)
B{x|10x1}(конечное множество чисел, больших 1, но меньших 10)
M{x|11x0, x∈N}(конечное множество натуральных чисел меньших 11, но больших 0)

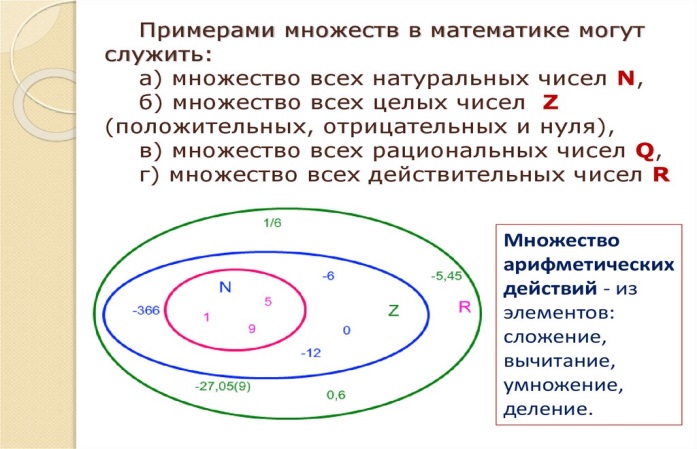
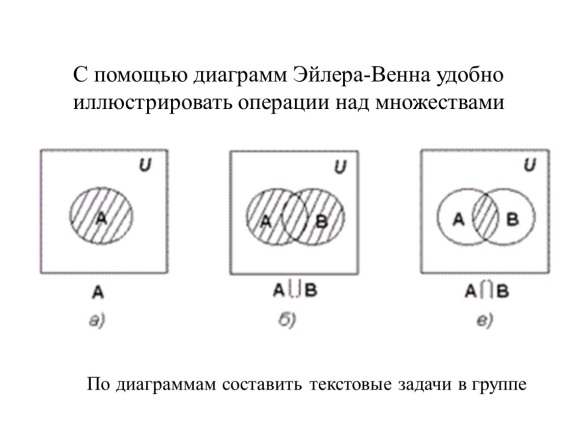
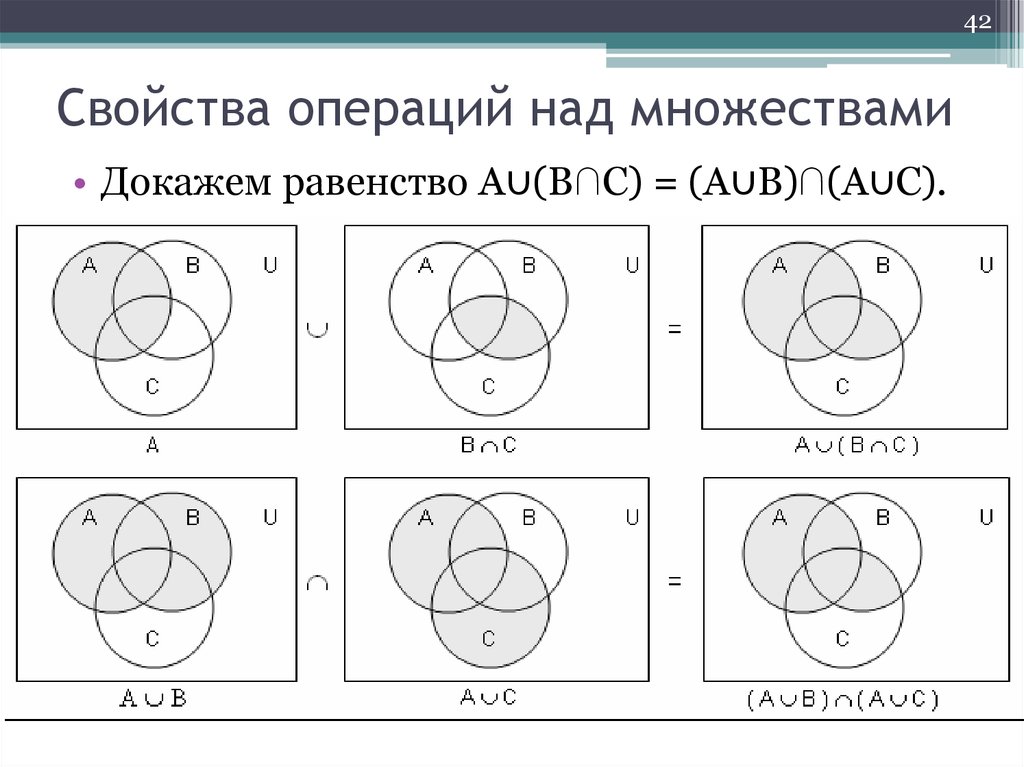
2.1.2.Визуализация множеств
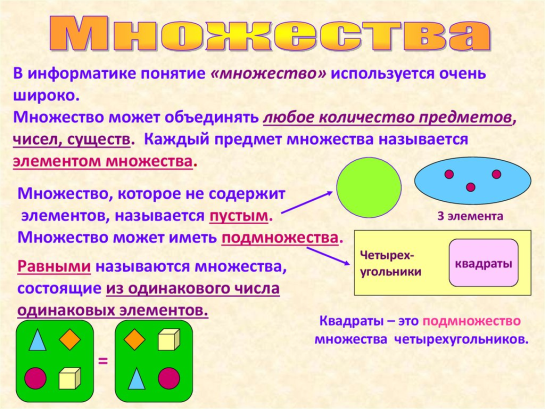

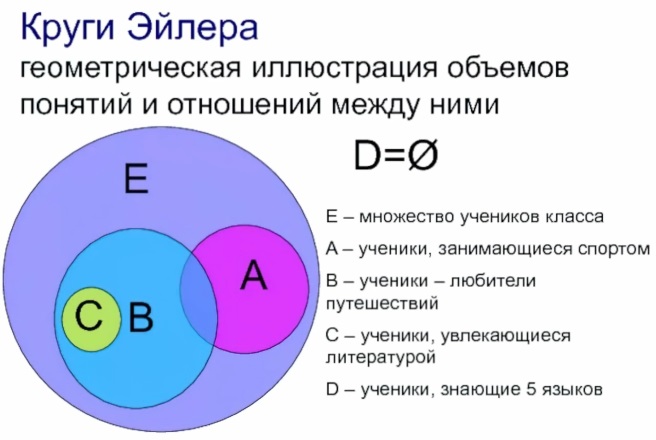
2.2. Практическая часть
Чтобы узнать, как много ученики моего класса знают о множествах, я провел опрос перед исследовательской работой, затем после того, как познакомил их с содержанием работы
2.2.1. Опрос.
| № п/п | Вопросы | Опрошено _25___ человек | Опрошено _25___ человек |
| до | после | ||
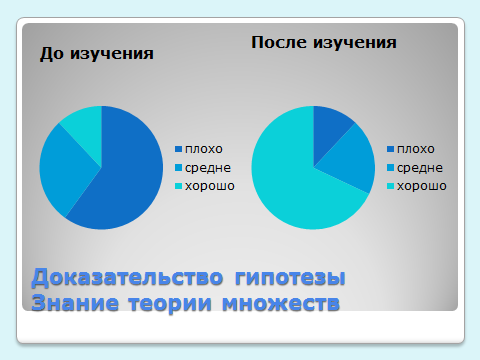
| 1. | Как вы считаете, хорошо ли вы знаете тему «множества»? |
|
|
| а) Хорошо | 3 | 17 | |
| б) Средне | 7 | 5 | |
| в) Плохо | 15 | 3 | |
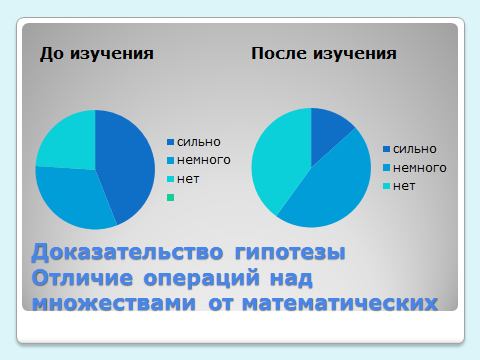
| 2. | Отличаются ли операции над множествами от обычных математических? |
|
|
| а) Да, сильно | 11 | 2 | |
| б) Да, немного | 8 | 7 | |
|
| в) Нет | 6 | 16 |
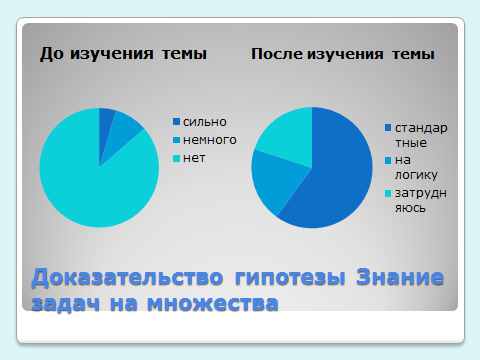
| 3. | Какие методы решения задач на множества вы знаете? |
|
|
| а) Стандартные | 4 | 15 | |
| б) Решаю на основе логики | 2 | 5 | |
| в) Затрудняюсь ответить | 19 | 5 | |
| 4. | Сможете ли вы четко сформулировать ваш способ решения? |
|
|
|
| а) Да | 5 | 16 |
|
| б) Нет | 20 | 9 |
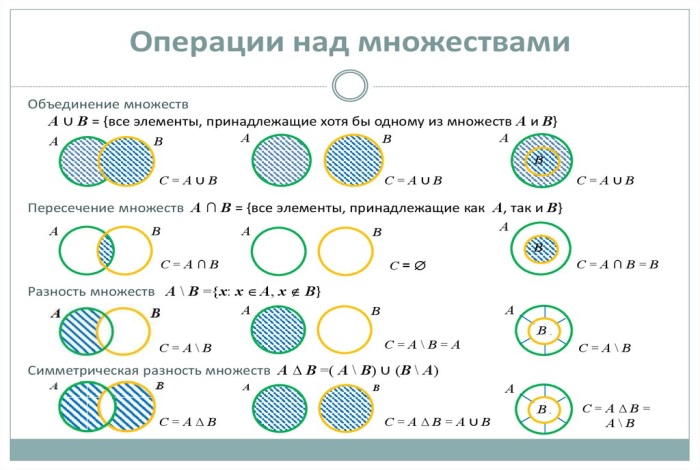
2.2.2 Арифметические действия и операции над множествами
Рассмотрим несколько элементарных операций.
Сложение – Пересечение.
Операция пересечение (обозн. ⋂) – при выполнении для множеств А и В,
Получаем множество С, содержащее элементы, принадлежащие и А, и В одновременно.
Сложение – Объединение.
Операция объединение (обозн. ∪) – при выполнении для множеств А и В, получаем множество С, содержащее элементы, принадлежащие или А, или В.
Вывод.
Арифметическое действие «Сложение» интерпретируется операциями «Пересечение» и «Объединение», с различными результатами.
То есть имеет место различие.
Вычитание – Разность.
Операция разность (обозн. \) – при выполнении для множеств А и В, получаем множество С, содержащее элементы А, которые не принадлежат В.
Вывод.
Арифметическое действие «Вычитание» схоже с операцией «Разность».
То есть имеем сходство.
Сравнение – Надмножества и подмножества.
Знак ⊂ (Является подмножеством) – для множеств А и В означает: «каждый элемент из ![]() также является элементом из
также является элементом из ![]() ».
».
Знак ⊃ (Является надмножеством) – для множеств А и В означает: «каждый элемент из ![]() также является элементом из
также является элементом из ![]() .
.
Вывод.
Сравнение в арифметике аналогичны знакам «Надмножество» и «Подмножество». То есть сходны.



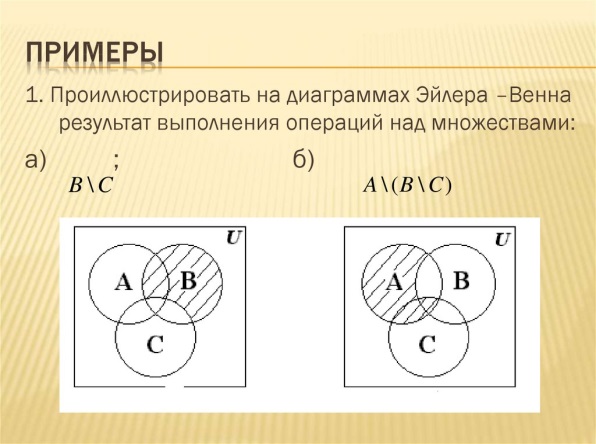
3. Вывод
Из опроса следует, что мои одноклассники очень мало знали о множествах. А решение задач с ними вызывали затруднения. Респонденты не смогли дать четкое объяснение способам решения. Решения были названы интуитивными. После ознакомления результат изменился
Исследования операций показали, что действия над множествами и обычные математические сходны.
3.1. Доказательство гипотезы
Вернёмся к гипотезе моей работы. Я предполагал, что ученики моего класса мало знают о множествах, их применении и решении задач с ними. Опрос показал, что очень немногие из учеников хорошо знали тему «Множества» и умели решать задачи по ней.
Решения свои респонденты не смогли обосновать. То есть подтвердилось мое предположение о решениях основанных на логике, а не на знаниях.
Исследования показали, что арифметические действия можно рассматривать как частный случай операций над множествами. То есть операции над множествами шире.
Можно сказать, что моя гипотеза полностью подтвердилась.
3.2. Продукт проекта
Продукт моей работы – сборник задач по данной теме (Приложение №1), рубрика «Это интересно!» (Приложение №2)
4. Заключение.
Моя гипотеза подтвердилась полностью. Арифметические действия отличаются от операций над множествами, однако, основаны на них.
В процессе работы были рассмотрены следующие вопросы:
основные положения теории множеств ( определение множества, конечные и бесконечные множества, обозначения множеств, способы их задания, подмножество);
наглядные примеры (помогли мне лучше усвоить понятия).
В настоящее время теория множеств является одной из основ различных областей математики ( функциональный анализ, топология, общая алгебра). Ведутся глубокие исследования и в самой теории множеств. Эти исследования связаны с самыми основами математики.
Элементами теории множеств могут быть самые разнообразные предметы: виды и подвиды животных, растений; буквы; атомы; числа; функции; точки; углы и т.д. Отсюда с самого начала ясна чрезвычайная широта теории множеств и ее прикладное значение к очень многим областям знаний (математика, биология, физика, экология). Теория множеств является истоком для многих современных наук, Поэтому так важно усвоить тему «Множества» в школьном курсе.
Моя работа может служить учебным пособием на уроках математики, связанных с темой “множества”.
Литература:
Виленкин Н.Я. Рассказы о множествах. – М.: Наука, 1965.
Жарковская Н.А. Георг Кантор и теория множеств.
Корн Г., Корн Т. Справочник по математике. - М.: Наука, 1974.
Школьная энциклопедия. Математика / Под ред. С.М. Никольского. – М.: Большая российская энциклопедия, 1996.
https://distant.msu.ru/pluginfile.php/210847/mod_resource/content/1/Лекция%20№1.Множества.pdf
https://maximumtest.ru/
https://yandex.ru/video/preview/9966156137097079833?text=множества%206%20класс%20математика&path=yandex_search&parent-reqid=1737015941063941-1763960444186257529-balancer-l7leveler-kubr-yp-vla-176-BAL&from_type=vast
https://infourok.ru/prezentaciya-po-matematike-na-temu-mnozhestva-operacii-nad-mnozhestvami-6-klass-4575671.html
Приложение №1.
Сборник задач.
Задача 1
1. Запишите на символическом языке следующее утверждение:
а) число 22 – натуральное;
б) число –9 не является натуральным;
в) число –10 является целым;
г) число 4,5 – не целое.
Задача 2
1. Даны множества: А = {1; 4; 9}, В = {1; 4; 9; 21},
С = {6; 21}.
Найдите: 1) А∩В; 2) А∩С; 3) С∩В.
Задача 3
1. Даны множества: А = {a, b, c, d}, B = {c, d, m,k},
C = {c, m, n, p}. Найдите (А∩В)∩С.
2. Разность А и В это множество элементов А, не принадлежащих В.
Разность А и В обозначают так: А\ В.
Например, если А = {2; 4; 6; 8; 10} и В = {5; 10; 15; 20}, то А\ В={2; 4; 6; 8}.
Задача 4
Каждая семья нашего класса ходит в кино или в кафе, или и то и другое вместе. 21 семей ходят в кино, а 17 семей ходят в кафе и лишь 13 ходят и в кино и в кафе. Сколько семей в нашем классе?
Задача 5
На школьной спартакиаде каждый из 25 учеников нашего класса выполнил норматив или по бегу, или по прыжкам в высоту. Оба норматива выполнили 7 человек, а 11 учеников выполнили норматив по бегу, но не выполнили норматив по прыжкам в высоту. Сколько учеников выполнили норматив: а) по бегу; б) по прыжкам в высоту; в) по прыжкам при условии, что не выполнен норматив по бегу?
Задача 6
Каждый из учеников нашего класса в зимние каникулы ровно два раза был в кино, посмотрев фильм «Финист-первый богатырь», «Мегаполис», «Охота на ворон-2», эти фильмы видели соответственно 15, 12 и 13 учеников. Сколько учеников в классе?
Задача 7
В воскресенье 19 учеников нашего класса побывали в Пипл-парке, 10 – в цирке и 6 – на стадионе. Пиплс-парк и цирк посетили 5 учеников; Пиплс-парк и стадион-3; цирк и стадион -1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а 5 учеников не посетили ни одного места?
Задача 8
В нашем классе 25 учеников. Из них 7 любят мандарины,
11 – апельсины. Двое любят мандарины и апельсины; 6 – мандарины и яблоки; 5 – яблоки и апельсины. Но есть в классе два ученика, которые любят всё и четверо таких, что не любят фруктов вообще. Сколько учеников нашего класса любят яблоки?
Задача 9
На уроке литературы учитель решил узнать, кто из 40 учеников 9 –го класса читал книги А, В, С. Результаты опроса выглядели так: книгу А прочитали 25 учеников, книгу В – 22 ученика, книгу С – 22 ученика; одну из книг А или В прочитали 33 ученика, одну из книг А или С прочитали 32 ученика, одну из книг В или С – 31 ученик.
Все три книги прочитали 10 учеников.
Сколько учеников:
А) прочитали только по одной книге;
Б) прочитали ровно две книги;
В) не прочли ни одной из указанных книг?
Задача 10
На зимних каникулах из 25 учащихся класса только двое просидели дома, а 14 ребят ходили в кино, 4 – в театр, 6 – в цирк. Кино и театр посетили 2 человека, кино и цирк –3, театр и цирк – 4. Сколько ребят побывало и в кино, и в театре, и в цирке?
Приложение №2
«Это интересно!»
Биография Л.Эйлера

Леонард Эйлер родился 15 апреля 1707 года в швейцарском городе Базеле. Его отец, интересуясь математикой, привил этот интерес и сыну.
До 13 лет Леонард обучался дома, затем поступил на философский факультет в Базеле, где познакомился с Иоганном Бернулли, преподавателем элементарной математики и астрономии. Тот, заметив интерес мальчика к своим предметам, начал заниматься с ним дополнительно.
В 1723 году Леонард Эйлер получил степень магистра и приступил к изучению восточных языков и богословия. Однако изучение математики и общение с Бернулли продолжились.
В 1725 году братья Бернулли стали членами Петербургской академии наук, основанной Екатериной I, а спустя год выслали приглашение и Эйлеру. В Петербурге для молодого математика сложились благоприятные условия.
В 1731 году Леонард Эйлер получил звание профессора физики и стал действительным членом Академии. В 1733 году он возглавил кафедру высшей математики.
ЭЙЛЕР (Euler) математик, механик, физик и астроном.
По происхождению швейцарец. В 1726 был приглашен в Петербургскую АН и переехал в 1727 году в Россию. Был адъюнктом (1726), а в 1731-41 и с 1766 академиком Петербургской АН (в 1742-66 иностранный почетный член) . В 1741-66 работал в Берлине, член Берлинской АН. Эйлер — ученый необычайной широты интересов и творческой продуктивности. Автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и других, оказавших значительное влияние на развитие науки.
Эйлер скончался в 1783 году от апоплексического удара. Похоронен он был в Петербурге на Смоленском кладбище (сейчас его прах находится в некрополе Александро-Невской лавры) . Три сына его и их дети остались в России.
В 1735 году, выполняя сложную работу по расчёту траектории кометы и затратив на это всего три дня, Эйлер заболел нервной горячкой и лишился правого глаза. К 1771 году Эйлер полностью потерял зрение, но благодаря ученикам и помощникам продолжал интенсивно работать.
Скончался Леонард Эйлер 18 сентября 1783 года в Санкт-Петербурге от апоплексического удара и был похоронен на Смоленском лютеранском кладбище.
Биография Бенуа Мандельброта.
Б енуа́ Мандельбро́т — французский и американский математик, создатель фрактальной геометрии. Лауреат премии Вольфа по физике (1993).
енуа́ Мандельбро́т — французский и американский математик, создатель фрактальной геометрии. Лауреат премии Вольфа по физике (1993).
Бенуа Мандельброт родился в Варшаве в 1924 году в семье литовских евреев. Его мать была врачом, а отец галантерейщиком. Зато брат отца Шолем Мандельброт жил во Франции и был достаточно известным математиком, входившим группу, известную научному сообществу под общим псевдонимом «Никола Бурбаки». Когда Бенуа было 12 лет, он с семьей эмигрировал в Париж, где как раз жил Шолем Мандельброт. Вскоре после начала Второй мировой войны Бенуа с семьей снова переехал — теперь на юг Франции, в городок Тюль. Там он наконец пошел в школу, но успеха в освоении учебной программы добился не сразу.
Учиться в школе было неинтересно, и потому к шестнадцати годам Бенуа Мандельброт еле знал алфавит и таблицу умножения до пяти. Говорят, что до конца своих дней ученый с трудом пользовался телефонным справочником.
Однако, как и у его дяди Шолема, у Бенуа проявился интерес к математике и, более того, обнаружилось великолепное пространственное воображение. Даже чисто алгебраические задачи ему удавалось решать геометрическим способом. Такая оригинальность решений позволила молодому Бенуа поступить в Сорбонну. Окончив университет, он уехал в США, где окончил Калифорнийский технологический институт. После этого вернулся во Францию и получил докторскую степень. В 1955 году он женился на Альетт Каган и переехал в Женеву. Через три года Мандельброт окончательно перебрался в США.
Желанием Мандельброта было уйти в своих исследованиях как можно дальше от официальной академической науки. Свое намерение ученому удалось начать реализовывать начиная с 1958 года. Именно тогда Бенуа Мандельброт приступил к работе в научно-исследовательском центре IBM в Йорктауне и смог заниматься не только чисто прикладными проблемами компании.
Мандельброт с удовольствием менял одну тему на другую и за несколько лет успел поработать в области лингвистики, теории игр, экономики, аэронавтики, географии, физиологии, астрономии, физики.
«Иногда меня охватывает внезапный порыв, и я бросаю исследования на середине, чтобы снова погрузиться в новую область, которая внезапно стала для меня интересной и в которой я не знаю ничего, — говорил ученый. — Я следовал моим инстинктам…»
Так, исследуя экономику, Бенуа Мандельброт обнаружил, что, внешне произвольные, колебания цены могут следовать скрытому математическому порядку во времени, который не описывается стандартными кривыми. Изучив динамику цен на хлопок за период более ста лет, он выяснил тенденцию их изменения, хотя они казались случайными. Мандельброт удивил экономистов тем, что проследил симметрию как длительных, так и кратковременных колебаний цены.
Такая бурная деятельность в разных областях наук позволила Мандельброту в середине 1960-х годов разработать теорию так называемой фрактальной геометрии, или геометрии природы. Целью фрактальной геометрии был анализ сломанных, «морщинистых» и нечетких форм.
Для описания таких объектов Мандельброт придумал слово «фрактал», которое происходит от латинского слова fractus — «сломанный» или «разбитый». Самой значимой работой Мандельброта считается книга «Фрактальная геометрия природы».
Мандельброт был профессором математических наук, почетным преподавателем Йельского Университета, баттельским членом Тихоокеанской национальной лаборатории. Он был очень уважаемым ученым, выступал с лекциями на нобелевских банкетах. Сегодня ученые пытаются расширить область фрактальной геометрии так, чтобы она могла быть применена практически ко всему в мире — от предсказания цен на рынке ценных бумаг до совершения новых открытий в теоретической физике. Умер 14 октября 2010 года в Кембридже (Массачусетс, США), в возрасте 85 лет.
3 .Наивная теория множеств
Георг Кантор (1845 - 1918), основатель теории множеств
До второй половины 19 века понятие "множества" не рассматривалось как математическое ("множество книг на полке", "множество человеческих добродетелей" и т. д. - все это чисто бытовые обороты). Положение изменилось, когда немецкий математик Георг Кантор разработал свою программу стандартизации математики, в рамках которой любой математический объект должен быть той или иной "множеством" [1] [2]. Например, натуральное число за Кантором следовало рассматривать как множество, состоящее из единственного элемента другого множества, называемой "натуральным рядом", который, в свою очередь, сам является множеством, удовлетворяющей так называемым аксиомам Пеано. При этом общему понятию "множества", что рассматривалось им как центральное для математики, Кантор давал весьма размыты определение, что "множество есть многое, мыслимое как единое", и т. д. Это вполне соответствовало намерения самого Кантора, который подчеркнуто называл свою программу не "теорией множеств" (этот термин появился много позже), а "учением о множествах" (Mengenlehre).
Программа Кантора вызвала резкие протесты со стороны многих современных ему известных математиков. Особенно выделялся своим непримиримым к ней отношением Леопольд Кронекер, который считал, что математическими объектами могут считаться лишь натуральные числа и то, что к ним непосредственно сводится (известна его фраза о том, что "бог создал натуральные числа, а все остальное - дело рук человеческих"). Полностью отвергли теорию множеств и такие авторитетные математики, как Герман Шварц и Анри Пуанкаре. Однако, некоторые другие математики - в частности, Готлоб Фреге, Рихард Дедекинд и Давид Гильберт - поддержали Кантора в его намерении перевести всю математику на теоретико-множественную язык. В частности, теория множеств стала основой: теории меры, топологии, функционального анализа.
Однако вскоре выяснилось, что направление Кантора на отсутствие ограничений при операциях с множествами (выраженное им самим в принципе "суть математики заключается в ее свободе") несовершенна изначально, а именно, было найдено ряд теоретико-множественных антиномий : оказалось, что при использовании теоретико-множественных представлений некоторые утверждение могут быть доказаны вместе со своими возражениями (а тогда, согласно правилам классической логики высказываний, может быть "доказано" абсолютно любое утверждение). Антиномии ознаменовали собой полный провал программы Кантора.
4. Аксиоматическая теория множеств
Эрнст Цермело (1871 - 1953), основатель, автор аксиоматики теории множеств.
В 1901 году Бертран Расселл, изучая наивную теорию множеств, пришел к парадоксу (с тех пор известному как парадокс Рассела). Таким образом была продемонстрирована противоречивость наивной теории множеств и, связанной с ней канторской программы стандартизации математики. Аксиоматическая теории множеств была первоначально разработана, чтобы избавиться от таких парадоксов в теории множеств. [3]
После обнаружения антиномии Рассела часть математиков (например, Л. Э. Я. Брауэр и его школа) решила полностью отказаться от использования теоретико-множественных представлений.
Другая часть математиков, возглавленная Давидом Гильбертом сделала ряд попыток обосновать ту часть теоретико-множественных представлений, которая казалась им меньше ответственным за возникновение антиномий, на основе надежной финитной математики.
Логический аппарат усовершенствовал Бертран Рассел в работах, позднее собранных в его монографии "Principia Mathematica" (1910-1913). И в 1904-1908 годах Эрнст Цермело предложил первую из аксиоматической теории множеств.
Особенностью аксиоматического подхода является отказ от заложенного в программу Кантора представление о настоящем существование множеств в некотором идеальном мире. В рамках аксиоматических теорий множества "существуют" исключительно формальным образом, и их "свойства" могут существенно зависеть от выбора аксиоматики. Этот факт всегда был мишенью для критики со стороны тех математиков, которые не соглашались (как на том настаивал Гильберт) признать математику, лишенной всякого содержания, игрой в символы. В частности, М. М. Лузин писал, что "мощность континуума, если только мыслить его как множество точек является некая единая реальность", место которой в ряду кардинальных чисел не может зависеть от того, признается как аксиома континуум-гипотеза, или ее отрицание.
Сейчас распространенной аксиоматической теорией множеств является ZFC - теория Цермело-Френкеля с аксиомой выбора. Вопрос о непротиворечивости этой теории (а тем более - о существовании модели для нее) остается нерешенным.
15

 Получите свидетельство
Получите свидетельство Вход
Вход











 Множества и операции над ними (2.19 MB)
Множества и операции над ними (2.19 MB)
 0
0 205
205 3
3 Нравится
0
Нравится
0



