6
Филиал Областного государственного бюджетного образовательного учреждения среднего профессионального образования
« Рязанский педагогический колледж» в г. Касимове
(Филиал ОГБОУ СПО РПК в г. Касимове)
Рабочая программа
учебной дисциплины
Математика
Специальность 050144 Дошкольное образование
г. Касимов
2014
Рабочая программа учебной дисциплины Математика разработана на основе Федерального государственного образовательного стандарта по специальностям среднего профессионального образования (СПО)
050144 Дошкольное образование
При составлении программы были использованы разъяснения по формированию примерных программ учебных дисциплин начального профессионального и среднего профессионального образования, составленные на основе Федеральных государственных стандартов начального профессионального и среднего профессионального образования, утверждённые И.М. Реморенко.
Организация-разработчик: филиал ОГБОУ СПО РПК в г. Касимове
Разработчик:
Преподаватель математики филиала ОГБОУ СПО РПК в г. Касимове
Колоколенкова И.И.
Утверждаю:
заведующая учебной частью
филиала «РПК» в г. Касимове
____________ О.В. Матвеева
Рекомендована ПЦК психолого-педагогических дисциплин и частных методик ОГБОУ СПО РПК в г. Касимове
Протокол №____________ от «____»__________2014 г.
Председатель ПЦК_________________/Колоколенкова И.И.
СОДЕРЖАНИЕ
| |
|
- ПАСПОРТ рабочей ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ
| 4 |
- СТРУКТУРА и содержание УЧЕБНОЙ ДИСЦИПЛИНЫ
| 6 |
- условия реализации программы учебной дисциплины
| 11 |
- Контроль и оценка результатов Освоения учебной дисциплины
| 12 |
1. Паспорт рабочей программы учебной дисциплины Математика.
1.1 Область применения программы.
Программа учебной дисциплины Математика является частью основной профессиональной образовательной программы в соответствии с ФГОС по специальностям СПО.
Программа учебной дисциплины Математика может быть использована в дополнительном профессиональном образовании в рамках реализации программ переподготовки кадров в учреждениях СПО.
Специальность СПО –
050144 Дошкольное образование.
1.2. Место дисциплины в структуре основной профессиональной образовательной программы:
В соответствии с ФГОС по специальностям среднего профессионального образования (СПО) учебная дисциплина Математика - частью учебного цикла ЕН.00 Математический и общий естественнонаучный цикл.
1.3 Цели и задачи дисциплины – требования к результатам его освоения.
Учебная дисциплина Математика предназначена для подготовки студентов – будущих воспитателей – к обучению математике в ДОУ, а также быть базой для дальнейшего образования. В процессе изучения студентами должны быть глубоко и прочно усвоены основные понятия курса начальной математики. Это изучение должно способствовать также формированию представлений о математике, и совершенствованию логической культуры студентов педагогического колледжа.
В результате освоения дисциплины обучающийся должен:
уметь:
- применять математические методы для решения профессиональных задач;
- решать текстовые задачи;
- выполнять приближенные вычисления;
- проводить элементарную статистическую обработку информации и результатов исследований, представлять, полученные данные графически;
знать:
- понятие множества, отношения между множествами, операции над ними;
- понятие величины и ее измерения;
- историю создания систем единиц величины;
- этапы развития понятий натурального числа и нуля;
- системы счисления;
- понятие текстовой задачи и процесса ее решения;
- историю развития геометрии;
- основные свойства геометрических фигур на плоскости и в пространстве;
- правила приближенных вычислений;
- методы математической статистики.
1.4. Рекомендуемое количество часов на освоение интегрированной программы.
Согласно учебному плану, составленному на основе ФГОС на учебную дисциплину Математика, входящую в математический и общий естественнонаучный цикл (ЕН), отводится 80 часов.
Максимальная учебная нагрузка обучающегося - 120 час, в том числе:
- обязательная учебная нагрузка обучающегося – 80 часов;
- самостоятельная работа обучающегося –40 часа.
2. Структура и содержание учебной дисциплины.
2.1. Объем учебной дисциплины и виды учебной работы
| Вид учебной работы | Объем часов |
| Максимальная учебная нагрузка (всего) | 120 |
| Обязательная аудиторная учебная нагрузка (всего) | 80 |
| в том числе: |
|
| практические занятия | 65 |
| контрольные работы | 6 |
| курсовая работа (проект) (если предусмотрено) | - |
| Самостоятельная работа обучающегося (всего) | 40 |
| в том числе: |
|
| - самостоятельная работа с учебной литературой; | 8 |
| - написание докладов; | 16 |
| - самостоятельная работа по решению практических задач, ситуаций; | 16 |
2.2. Тематический план и содержание учебной дисциплины
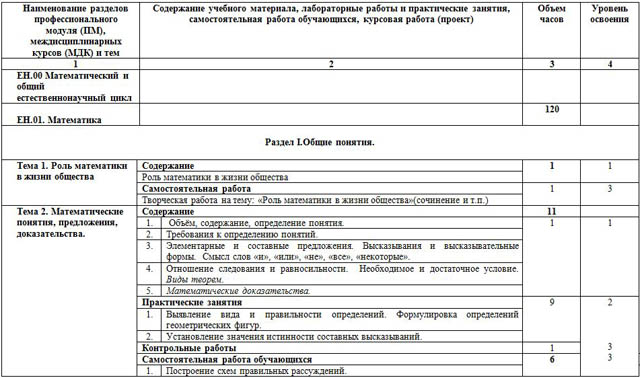
| Наименование разделов профессионального модуля (ПМ), междисциплинарных курсов (МДК) и тем | Содержание учебного материала, лабораторные работы и практические занятия, самостоятельная работа обучающихся, курсовая работа (проект) | Объем часов | Уровень освоения |
|
| 1 | 2 | 3 | 4 |
|
| ЕН.00 Математический и общий естественнонаучный цикл |
|
|
|
|
|
ЕН.01. Математика |
| 120 |
|
|
|
Раздел I.Общие понятия.
|
|
| Тема 1. Роль математики в жизни общества | Содержание | 1 | 1 |
|
| Роль математики в жизни общества |
|
| Самостоятельная работа | 1 | 3 |
|
| Творческая работа на тему: «Роль математики в жизни общества»(сочинение и т.п.) |
|
| Тема 2. Математические понятия, предложения, доказательства. | Содержание | 11 |
|
|
| 1. | Объём, содержание, определение понятия. | 1 | 1
|
|
| 2. | Требования к определению понятий. |
|
| 3. | Элементарные и составные предложения. Высказывания и высказывательные формы. Смысл слов «и», «или», «не», «все», «некоторые». |
|
| 4. | Отношение следования и равносильности. Необходимое и достаточное условие. Виды теорем. |
|
| 5. | Математические доказательства. |
|
| Практические занятия | 9 | 2
3 3 |
|
| 1. | Выявление вида и правильности определений. Формулировка определений геометрических фигур. |
|
| 2. | Установление значения истинности составных высказываний. |
|
| Контрольные работы | 1 |
|
| Самостоятельная работа обучающихся | 6 |
|
| 1. | Построение схем правильных рассуждений. |
|
| 2. | Построение отрицаний высказываний, содержащих кванторы |
|
|
| 3. | Составление определений, соответствующим требованиям. |
|
|
|
|
| 4. | Доказательства |
|
|
|
| Тема 3. Понятие текстовой задачи и процесса ее решения.
| Содержание | 14 |
|
|
| 1. | Понятие текстовой задачи. Способы решения задачи. | 1 | 1 |
|
| 2. | Этапы решения задач арифметическим способом. |
|
| 3. | Решение задач алгебраическим способом. |
|
| 4. | Приёмы проверки решения задачи. |
|
| 5. | Решение задач другими способами. |
|
|
| Практические занятия | 12 | 2
3 |
|
| 1. | Решение задач разными способами. |
|
| Контрольные работы | 1 |
|
| Самостоятельная работа обучающихся | 6 |
|
| 1. | Решение нестандартных задач. |
|
| 2. | Составление и решение задач на экологическую тему. |
|
| 3. | Составление и решение задач с использованием регионального компонента. |
|
|
| 4. | Составление и решение задач на профессиональную тему. |
|
|
|
| Тема 4. Элементы теории множеств.
| Содержание | 16 |
|
|
| 1. | Понятие множества и элемента множества. Способы задания множеств. | 2 | 1 |
|
| 2. | Отношение между множествами. Пересечение и объединение множеств. |
|
| 3. | Дополнение подмножества. Понятие разбиения множества на классы. |
|
| 5. | Декартово произведение множеств. |
|
| Практические занятия | 13 | 2
|
|
| 1. | Нахождение объединения, пересечения, дополнения подмножества до множества. |
|
| 2. | Установление принадлежности элементов различным множествам. |
|
| 3. | Изображение декартова произведения на координатной плоскости. |
|
| 4. | Решение задач с помощью кругов Эйлера. |
|
| Контрольные работы | 1 |
3 |
|
| Самостоятельная работа обучающихся | 7 |
|
| 1. | Решение комбинаторных задач. |
|
| 2. | Сообщение о Леонарде Эйлере. |
|
|
| 3. | Решение комбинаторных задач с помощью кругов Эйлера. |
|
|
| Тема 5. Этапы развития понятий натурального числа и нуля.
| Содержание | 6 |
|
|
| 1. | Об истории возникновения понятий натурального числа и нуля. | 1 | 1 |
|
| 2. | Порядковые и количественные натуральные числа. |
|
| 3. | Теоретико-множественный смысл количественного натурального числа и нуля. |
|
| 4. | Смысл натурального числа и действий над числами – результатами измерения величин. |
|
| Практические занятия | 5 | 2
3 |
|
| 1. | Решение задач и обоснование выбора действий, используя терминологию как теоретико-множественную, так и принятую в начальном курсе математики. |
|
| 2. | Доказательство свойств арифметических действий над целыми неотрицательными числами. |
|
| Самостоятельная работа обучающихся | 3 |
|
| 1. | Сообщение о возникновении счёта у разных народов мира. |
|
|
| 2. | Простые и составные числа. Дружественные и совершенные числа (сообщения). |
|
|
| 3. | Нахождение простых чисел с помощью «решета Эратосфена» (сообщения) |
|
|
| Тема 6. Системы счисления.
| Содержание | 9 |
|
|
| 1. | Запись и чтение чисел в десятичной системе счисления. | 1 | 1 |
|
| 2. | Запись чисел в позиционных системах счисления, отличные от десятичной. |
|
| Практические занятия | 7 | 2
3 |
|
| 1. | Решение задач с использованием алгоритмов арифметических действий над многозначными числами. | 4 |
|
| 2. | Выполнение действий над числами в двоичной и троичной системах счисления. | 3 |
|
| Контрольная работа | 1 |
|
| Самостоятельная работа обучающихся | 3 |
|
| 1. | Выполнение действий над числами в системах счисления, отличных от десятичной. |
|
| 2. | Исторические сведения о системах счисления в разные времена.(сообщения) |
|
|
|
| Тема 7. Понятие величины и ее измерения.
| Содержание | 7 |
|
|
| 1.
| Понятие величины и измерения величины. Свойство скалярных величин. Правила выполнения действий над величинами. | 1 | 1 |
|
| 2. | Длина отрезка и ее измерение. |
|
| Площадь фигуры и ее измерение. |
|
| 3. | Масса тел, ее основные свойства и измерение. |
|
| Время, его свойства и измерение. |
|
| Практические занятия | 6 |
|
|
| 1. | Решение задач на зависимости между величинами. |
|
| Самостоятельная работа обучающихся | 3 |
|
| 1. | История возникновения системы единиц величин (сообщения). |
|
| 2. | Характеристика Международной системы единиц (СИ) (по учебнику). |
|
| Тема 8. Элементы математической статистики
| Содержание | 7 |
|
|
| 1. | Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка, среднее арифметическое, медиана. | 1 | 1 |
|
| 2. | Понятие о задачах математической статистики. |
|
| Практические занятия | 5 | 2 |
|
| 1. | Проведение элементарной статистической обработки информации и результатов исследований, представление, полученных данных графически. |
|
|
| Контрольная работа | 1 |
|
| Самостоятельная работа обучающихся | 3 | 3 |
|
| 1. | Проведение мониторинга различных видов деятельности при прохождении практики в детском учреждении дошкольного образования. |
|
| Тема 9. Свойства геометрических фигур на плоскости и в пространстве.
| Содержание | 9 |
|
|
| 1. | Историческое развитие геометрии. | 1 | 1 |
|
| 2. | Основные свойства геометрических фигур на плоскости и в пространстве. |
|
| Практические занятия | 7 | 2 |
|
| 1. | Нахождение площадей геометрических фигур. | 4 |
|
| 2. | Нахождение объёмов геометрических фигур. | 3 | 3
|
|
| Самостоятельная работа обучающихся | 4 |
|
| 1. | Оригами. |
|
|
| 2. | Платоновы тела. |
|
|
| 3. | Основоположники геометрии. Основы геометрии Н.И. Лобачевского (сообщения). |
|
|
| Контрольная работа | 1 |
|
|
3. Условия реализации междисциплинарного курса.
3.1. Требования к минимальному материально – техническому обеспечению
Реализация программы предполагает наличие учебного кабинета математики.
Оборудование учебного кабинета «Математика»:
комплект таблиц по математике;
комплект учебников по математике;
набор геометрических тел;
чертежные инструменты;
комплект дидактических материалов.
Технические средства обучения:
компьютер, проектор, фильмоскоп, эпидиаскоп, ксерокс и др.
3.2. Информационное обеспечение обучения.
Перечень рекомендуемых учебных изданий, Интернет – ресурсов, дополнительной литературы.
Основные источники:
Задачи для контрольных работ по математике: Для студентов фак. нач. классов пед. инст./ Стойлова Л.П., Лаврова Н.Н. и др.- М.: Просвещение, 1993
Сборник задач по математике: пособие для педучилищ Пышкало А.М., Стойлова Л.Н. и др.- М.: Просвещение, 1979.
Стойлова Л.П., Пышкало А.М. Основы начального курса математики. – М. Просвещение. 1988г.
Стойлова Л.В. Математика. М. Просвещение. 1991г.
Учебники по математике для начальных классов.
Новосельцева З.И. Развернутые планы лекций и учебные задания для студентов по курсу «Теоретические основы обучения математике»/С.-Петербург, Изд-во «Образование»,РГПУ, 1997
4. Контроль и оценка результатов освоения
учебной дисциплины
| Результаты обучения (освоенные умения, усвоенные знания) | Формы и методы контроля и оценки результатов обучения |
| В результате изучения обязательной части цикла обучающийся должен: уметь: применять математические методы для решения профессиональных задач; решать текстовые задачи; выполнять приближенные вычисления; проводить элементарную статистическую обработку информации и результатов исследований, представлять полученные данные графически; знать: понятия множества, отношения между множествами, операции над ними; понятия величины и ее измерения; историю создания систем единиц величины; этапы развития понятий натурального числа и нуля; системы счисления; понятия текстовой задачи и процесса ее решения; историю развития геометрии; основные свойства геометрических фигур на плоскости и в пространстве; правила приближенных вычислений; методы математической статистики
| Формы контроля обучения: – домашние задания проблемного характера; – практические задания по работе с информацией, документами, литературой; – подготовка и защита индивидуальных и групповых заданий проектного характера.
Формы оценки результативности обучения: - накопительная система баллов, на основе которой выставляется итоговая отметка. - традиционная система отметок в баллах за каждую выполненную работу, на основе которых выставляется итоговая отметка
Методы контроля направлены на проверку умения учащихся: – выполнять условия здания на творческом уровне с представлением собственной позиции; – делать осознанный выбор способов действий из ранее известных; – осуществлять коррекцию (исправление) сделанных ошибок на новом уровне предлагаемых заданий; – работать в группе и представлять как свою, так и позицию группы;
методы оценки результатов обучения: – мониторинг роста творческой самостоятельности и навыков получения нового знания каждым обучающимся – формирование результата итоговой аттестации по дисциплине на основе суммы результатов текущего контроля. |
Преподаватель ____Колоколенкова__И.И.________________________

 Получите свидетельство
Получите свидетельство Вход
Вход












 Рабочая программа учебной дисциплины "Математика" (специальность 050144 Дошкольное образование) (0.18 MB)
Рабочая программа учебной дисциплины "Математика" (специальность 050144 Дошкольное образование) (0.18 MB)
 0
0 1274
1274 173
173 Нравится
0
Нравится
0


