Методы решения тригонометрических уравнений
Квадратные тригонометрические уравнения
1 тип. 
Так как уравнение содержит одноименные функции sin x, то необходимо заменить sin x = y; y [-1; 1]. Тогда исходное уравнение принимает вид ay2 + by +c = 0, а это квадратное уравнение. Далее необходимо решить квадратное уравнение и найти его решение: y1, y2.
Вернуться к старой переменной и решить простейшие тригонометрические уравнения: sin x = y1 и sin x = y2.
Аналогично решаем уравнения, содержащие другие тригонометрические функции.
Пример: sin2 x + sin x – 2 = 0, заменим sin x = y, y [-1; 1]
y2 + y – 2 = 0 D = 9; y1 = 1 y2 = -2
Возвращаемся к старой переменной sin x = 1 x = /2 + 2n; nZ
sin x = - 2 решения нет, т.к. – 2 [-1; 1]
Решить самостоятельно:
3sin2x +2sin x – 8 = 0 2) sin2 2x + sin 2x – 2 = 0 3) 2 sin2(x/3) + sin (x/3) – 6 = 0
4) 2 sin2 x + sin x – 1 = 0 5) sin (x2) – 2sin (x2) + 1 = 0 6) 2cos2 x – cos x – 1 = 0
7) 2cos2 3x + cos 3x – 6 = 0 8) tg2 x – 3tg x – 4 = 0 9) tg2 (x/4) – tg (x/4) + 1 = 0
2 тип.  (1)
(1)
Так как уравнение содержит разноименные функции, то слагаемое содержащее квадрат, необходимо заменить, используя основное тригонометрическое тождество (в данном случае sin2 x = 1 – cos2 x). Раскрыть скобки, привести подобные слагаемые и свести уравнение (1) к первому типу квадратного тригонометрического уравнения.
Пример: 2sin2 x – cos x – 1 = 0,
заменим sin2 x = 1 – cos2 x и уравнение примет вид 2(1 – cos2 x) – cos x – 1 = 0
2 – 2cos2 x – cos x – 1 = 0
Приведем подобные слагаемые и получим уравнение -2cos2 x – cos x + 1 = 0
Далее решаем по схеме решения 1 типа квадратного тригонометрического уравнения, пусть cos x = y; y [-1; 1],тогда уравнение примет вид - 2y2 – y + 1 = 0 D = 9 y1 = - 1 и y2 = - ½.
Возврат к старой переменной и соответственно к простейшим тригонометрическим уравнения, которые имеют решения:
cos x = - 1 x = + 2n; nZ
cos x = - ½ x ± 2/3 + 2n; nZ
Решить самостоятельно:
10) 2 cos2 x - sin x + 1 = 0 11) 2 cos2(x/2) + sin (x/2) – 1 = 0 12) 4sin2 2x - cos 2x – 1 = 0
13) 2 sin2 (x2) +3 cos ( x2) = 0 14) tg x = ctg x
Метод введения вспомогательного аргумента
Уравнения вида  решаем способом введения вспомогательного аргумента, используя формулу
решаем способом введения вспомогательного аргумента, используя формулу 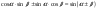 (1)
(1)
Выпишем коэффициенты  и
и  , вычислим
, вычислим 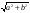
Разделить коэффициенты уравнения на  , после чего уравнение будет выглядеть
, после чего уравнение будет выглядеть 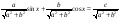 которое по формуле (1) представимо в виде
которое по формуле (1) представимо в виде
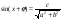
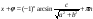 ;
;
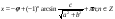 (2)
(2)
Угол находим из условия 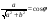
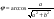 , где угол - угол первой координатной четверти.
, где угол - угол первой координатной четверти.
В значении корня уравнения (2) заменим его величиной.
Пример 2sin x + cos x = 2
Выпишем из уравнения a = 2 b = 1 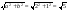
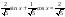
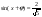
 ;
;

Вычислим угол из условия 

Ответ: 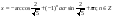
Решить самостоятельно:
15) sin x – cos x = 1 16) sin 2x + cos 2x = 1 17)  sin (x/3) + cos (x/3) = 2
sin (x/3) + cos (x/3) = 2
18) sin 5x + cos 5x = 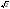
Однородное уравнение 1 степени
 (1) поделим каждое слагаемое уравнения на cos x ≠ 0, тогда уравнение (1)
(1) поделим каждое слагаемое уравнения на cos x ≠ 0, тогда уравнение (1)
корень уравнения находим по формуле простейшего тригонометрического уравнения:
Однородное уравнение 2 степени
(2) поделим каждое слагаемое уравнения на cos2 x ≠ 0. Тогда уравнение (2) будет выглядеть,
Решаем квадратное тригонометрическое уравнение относительно тангенса.
Примеры: а) sin 2x + cos 2x = 0: cos 2x ≠ 0 б) – sin2x – 5sinx cosx + 6 cos2x = 0:cos2x ≠ 0
tg 2x + 1 = 0 - tg2x – 5 tgx + 6 = 0
tg 2x = - 1 пусть tg x = y, y – любое число
2x = - /4 + n : 2 - y2 – 5 y + 6 = 0
x = -/8 + n; nZ D = 49 y1 = - 6 y2 = - 1
tg x = - 6 x = - arctg 6 + n; n Z
tg x = - 1 x = - /4 + n; n Z
Решить самостоятельно:
19) 20)
21) a 22)
23) 24)
Если в однородном уравнении 2 степени вместо нуля в правой части стоит число, то его необходимо умножить на 1, а её заменить основным тригонометрическим тождеством. Раскрыть скобки, перенести все слагаемые в левую часть и привести к стандартному виду однородности.
Пример:
Далее решаем по схеме решения однородного уравнения 2 степени и записываем ответ.
Решить самостоятельно:
25) 26)

 Получите свидетельство
Получите свидетельство Вход
Вход












 Методическое пособие по теме "Методы решения тригонометрических уравнений" (72.21 KB)
Методическое пособие по теме "Методы решения тригонометрических уравнений" (72.21 KB)
 0
0 651
651 27
27 Нравится
0
Нравится
0


