Методическая разработка по математике на тему: "Решение неравенств"

Введение

Цель современного образования - обучение и всестороннее развитие личности, способной к творчеству. Для достижения этой цели существует много программ, множество технологий обучения. В условиях современного развития и расширения доступности открытых информационных систем передача «готовых знаний» перестает быть главной задачей учебного процесса, снижается функциональная значимости привлекательность традиционной организации обучения. Основная задача обучения математике в школе - обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, не­обходимых в повседневной жизни дисциплин и продолжения образования. Хрошее математическое образование и развитие математических способностей необходимы не только тому, кто впоследствии займется научными исследованиями в области математики, но и тому, кто станет экономистом, организатором производства и так далее.

Неравенства встречаются на протяжении всего курса математики. С точки зрения математической логики неравенство является высказыванием. С помощью неравенства задаются основные числовые множества, формулируются определения предела, непрерывной функции, монотонной последовательности и функции, целого ряда других важных понятий. На языке неравенств нередко формулируется постановка задачи во многих приложениях математики. Во многих разделах математики, особенно в математическом анализе, в прикладной математике, неравенства встречаются значительно чаще, чем равенства. Но бывает, что для доказательства неравенства приходится использо­вать весьма тонкие геометрические или аналитические соображения. Полезно знать некоторые часто встречающиеся класси­ческие тождественные неравенства. Среди них - красивые неравенства, в которые переменные входят симметричным образом. Методы математического анализа, в свою очередь, удобное средство доказательства неравенств для функций от одной переменной.

1. Неравенства с одной переменной и их решения

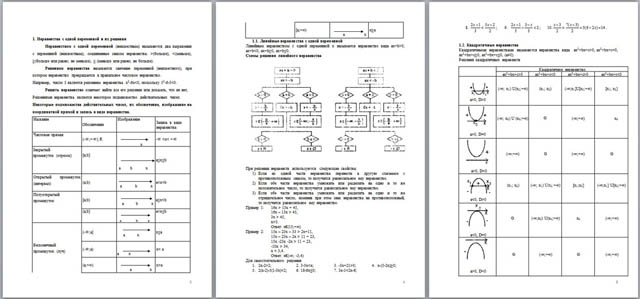
Неравенством с одной переменной (неизвестным) называются два выражения с переменной (неизвестным), соединенные знаком неравенства: >(больше), <(меньше), ≥(больше или равно; не меньше), ≤ (меньше или равно; не больше).

Решением неравенства называется значение переменной (неизвестного), при котором неравенство превращается в правильное числовое неравенство.

Например, число 5 является решением неравенства х² - 6х<0, поскольку 5² - 6 - 5<0.

Решить неравенство означает найти все его решения или доказать, что их нет,

Решениями неравенства является некоторое подмножество действительных чисел.

Весь материал – смотрите документ.