Получите свидетельство
Вход
Тип урока: урок систематизации и обобщения изученного материала
Цель урока:
Повторение, обобщение и проверка знаний по теме «Медиана, биссектриса, высота треугольника»;
Развитие у обучающихся внимания, логического мышления, настойчивости, самостоятельности, умения анализировать, сравнивать;
Развитие умения слушать и слышать, навыков математической грамотной речи;
Развитие рефлексивных умений учащихся.
Ход урока:
Организационный момент: приветствие, объявление темы и цели урока(2мин.)
Актуализация ранее изученного материала. Фронтальный опрос. (3мин.)
Сегодня мы продолжаем с Вами знакомство с медианой, биссектрисой и высотой треугольника.
Вначале я попрошу Вас вспомнить, какая геометрическая фигура называется треугольником? (учащиеся дают ответ)
Какие виды треугольников Вам известны? (учащиеся называют классификацию треугольников по сторонам и углам)
Дайте подробное определение каждого вида треугольника (учащиеся отвечают).
Что такое периметр треугольника? (учащиеся дают ответ)
Для того, чтобы проверить как вы уяснили что такое медиана, биссектриса и высота треугольника предлагаю ответить на вопросы теста №1. вам предложены три варианта определения для каждого понятия Вам необходимо выбрать верный и записать на листочке нужный шифр (номера верных ответов). На выполнение задания Вам отводится 3 минуты (+3мин. на обсуждение результатов теста).
Тест №1 – смотрите презентацию
Давайте проверим, что у Вас получилось. Учитель называет фамилии нескольких учащихся, которые называют свой шифр. Давайте еще раз сформулируем определение медианы, биссектрисы и высоты (учащиеся дают ответ, учитель на доске приклеивает плакаты с формулировкой определений). Исходя из этих определений, мы получаем верный шифр: 422. Прошу учащихся получивших верный шифр поднять руку ( тем самым я сразу могу отследить, кто из учащихся справился с заданием, а у кого оно вызвало затруднения).
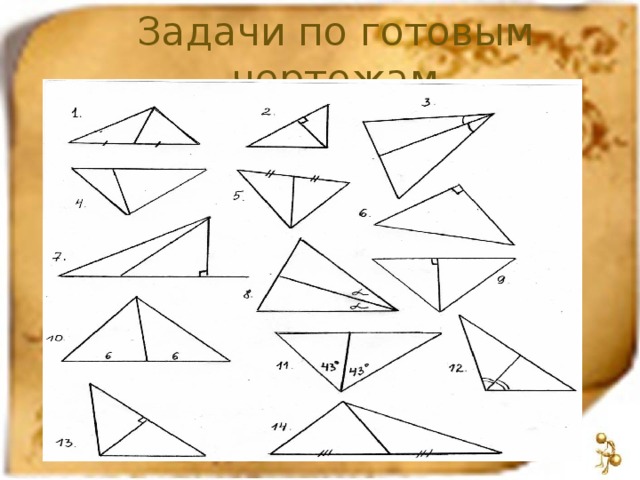
Работа по готовым чертежам.
Молодцы ребята, результаты теста показали, что Вы хорошо знаете определения. А вот следующее задание покажет, сможете ли вы на чертеже найти в каком треугольнике проведена высота, биссектриса или медиана. На доске имеются чертежи 14 треугольников. Сейчас ребята, сидящие на первом ряду, выпишут в тетрадь номера треугольников, в которых проведена высота. Сидящие на втором ряду выписывают номера треугольников, в которых проведена биссектриса, и сидящие на третьем ряду выпишут номера треугольников, в которых проведена медиана. На выполнение данного задания Вам отводится 3 минуты (+3мин. на обсуждение результатов).
Давайте проверим, что же у вас получилось. Приглашаю с каждого ряда по одному представителю (называю фамилии конкретных учащихся), каждому раздаю маркер своего цвета (красный, синий, зеленый) и предлагаю на чертеже обвести цветным маркером номер нужного треугольника. После завершения работы обсуждаем еще раз с учащимися правильные ответы.
В результате учащиеся первого ряда выбирают номер: 2,7,9,13; второго ряда: 3,8,11,12; третьего ряда: 1,5,10,14.
Прошу учащихся выбравших верные номера поднять руку (тем самым я сразу могу отследить, кто из учащихся справился с заданием, а у кого оно вызвало затруднения).
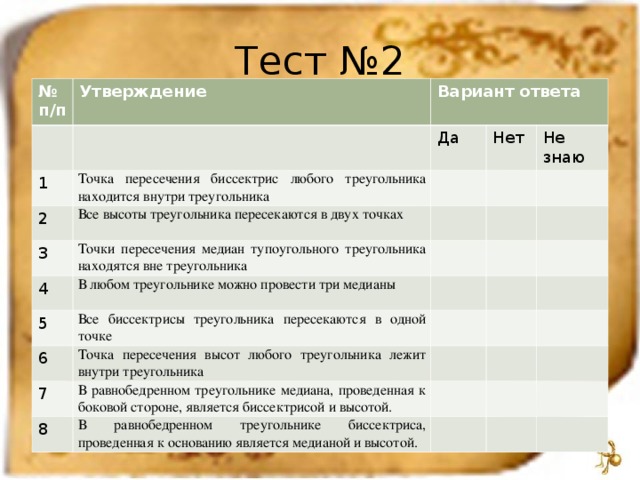
Медиана, биссектриса и высота треугольника обладают особыми свойствами. Тест №2 позволит нам выяснить, как же Вы эти свойства усвоили. Тест содержит восемь утверждений и три варианта ответа «да»- если утверждение верное, «нет»- если утверждение неверное и третий вариант ответа «не знаю». В течение следующих четырех минут вам предстоит определить истинность каждого утверждения и поставить галочку в нужное «окошко» (+3мин. на обсуждение результатов).
Тест №2 – смотрите презентацию
Давайте проверим, что же у Вас получилось. Какие утверждения из данного списка на Ваш взгляд являются верными? (называю фамилии учащихся, которые дают ответ). Таким же образом проверяем, какие утверждения является ложными. В итоге имеем: верные утверждения 1,4,5,8; ложные утверждения: 2,3,6,7. Прошу учащихся выбравших верные номера поднять руку (тем самым я сразу могу отследить, кто из учащихся справился с заданием, а у кого оно вызвало затруднения).
Молодцы ребята, вы очень хорошо справились и с этим заданием. А теперь нам предстоит применить наши знания на практике и решить задачи.
Решение задач на применение знаний на практике (10мин.)
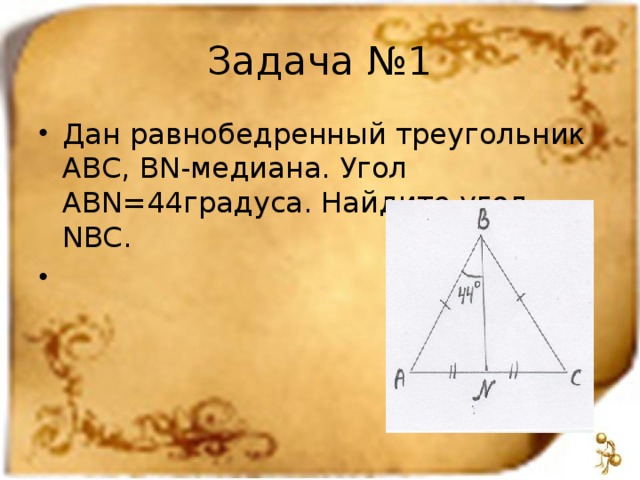
№1
Дан равнобедренный треугольник АВС, BN-медиана. Угол ABN=44 °. Найдите угол NBC.
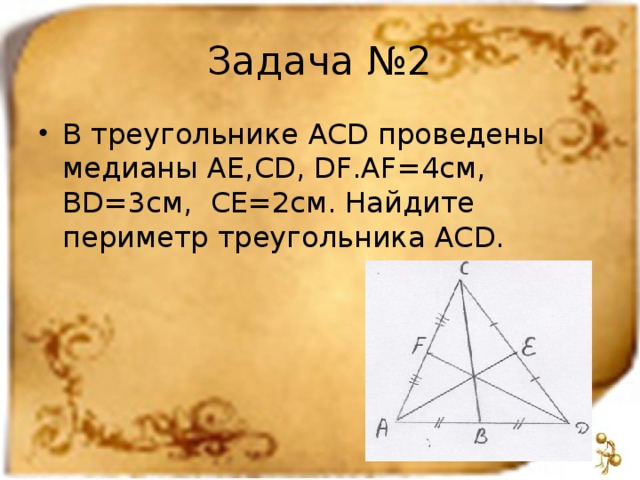
№2
В треугольнике ACD проведены медианы AE,CВ, DF.AF=4см, BD=3см, CE=2см. Найдите периметр треугольника ACD.
Подведение итогов урока (3мин.)
Какая цель стояла перед нами на уроке?
Достигли ли мы этой цели?
Что нового на уроке Вы узнали?
Осталось ли что – то непонятным?
Какое задание показалось самым сложным и почему?
Какое задание показалось самым интересным и почему?
Обсуждение домашнего задания : №119 из УМК автор Атанасян Л.С.(3мин.)
Этап - рефлексии : анкета «Продолжи предложение» (2мин.):
Анкета- рефлексия «Продолжи предложение»
( учащиеся по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске)
Сегодня я узнал…
Было интересно…
Было трудно…
Я выполнял задания…
Я понял, что…
Теперь я могу…
Я почувствовал, что…
Я приобрел…
Я научился…
У меня получилось…
Я смог…
Я попробую…
Меня удивило…
Мне захотелось…
Урок дал мне для жизни…
Список литературы
- Геометрия 7-9 классы. Тесты для текущего и обобщающего контроля. Ковалева Г.И., Мазурова Н.И., «Учитель», Волгоград, 2009
- Геометрия. Задачи на готовых чертежах для 7-9 классов. Балаян Э.Н., «Феникс», Ростов - на- Дону, 2006
- Контрольные работы, тесты, диктанты по геометрии. Фарков А.В., «Экзамен», Москва, 2009
- Сборник задач по геометрии в рисунках и тестах. 7-9 класс. Кукарцева Г.И. . «Аквариум», ГИППВ,2004
- Тесты. Геометрия. Дидактические материалы. 7класс. Короткова Л.М., Савинцева Н.В.. «Айрис Пресс», Москва, 2004
Медиана, биссектриса и высота треугольника (0.66 MB)
0
3991
937
Нравится
0
