В данной работе по геометрии содержатся признаки равенства треугольников, определения биссектрисы, медианы и высоты треугольника, равнобедренного треугольника и его свойства ;
есть задание на элементарное построения, в конце работы учащимся предлагается решить задачу на доказательство.
С помощью таких заданий очень хорошо видно, как учащиеся усвоили данную тему.
I вариант
Задание №1. Вставьте пропущенные слова.
1. Геометрическая фигура, имеющая 3 вершины, 3 стороны и 3 угла называется __________.
2. В равных треугольниках против соответственно равных сторон лежат _______________ углы.
3. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется .
4. Любой треугольник имеет всего ____ высоты.
5. Треугольник, у которого все стороны равны, называется ____________.
6. Равные стороны равнобедренного треугольника называются ___________ сторонами, а третья сторона – ____________.
7. Если две стороны и угол между ними одного треугольника соответственно равны ____________, то такие треугольники ________.
8. Высота равнобедренного треугольника, проведённого к основанию, является _________________.
9. Сумма длин трёх сторон треугольника называется его _______________.
10. В равнобедренном треугольнике углы при основании ______________.
11. Два треугольника называются равными, если их можно наложением ____________.
Задание №2.
Начертите треугольник. Постройте медианы данного треугольника и подпишите их.
Задание №3.
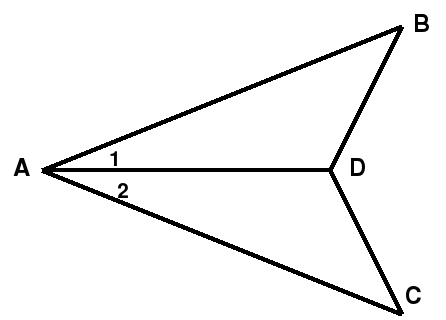
Докажите равенство треугольников АВС и ACD на рисунке, если АВ=АС и 1= 2.
II вариант
Задание №1. Вставьте пропущенные слова.
Точки С, Д, Е треугольника, изображённого на рисунке, называются _______ треугольника.
Из точки, не лежащей на прямой, можно провести перпендикуляр и притом только ______.
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей, противоположную сторону, называется ________ треугольника.
Любой треугольник имеет всего ______ медианы.
Отрезок биссектрисы угла треугольника, соединённый с точкой противоположной стороны, называется ______ треугольника.
Треугольник называется равнобедренным, у которого ______________.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны ____________,
то такие треугольники равны.
В равнобедренном треугольнике биссектриса, проведённая к основанию, является ________ и __________.
9. Если три стороны одного треугольника соответственно равны ________, то такие треугольники равны.
Любой треугольник имеет ____ биссектрисы.
Треугольник называется равносторонним, у которого __________
Задание №2.
Начертите остроугольный треугольник, обозначьте его. Постройте все его высоты.
Задание №3.
Докажите равенство треугольников АВС и ADС на рисунке, если ВС = АD и 1= 2.

 Получите свидетельство
Получите свидетельство Вход
Вход


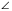 1=
1=









 Треугольники (31.17 КB)
Треугольники (31.17 КB)
 0
0 1085
1085 65
65 Нравится
0
Нравится
0


