Окружности
1. Основание 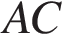 равнобедренного треугольника
равнобедренного треугольника 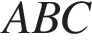 равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания
равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания 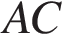 в его середине . Найдите радиус окружности, вписанной в треугольник
в его середине . Найдите радиус окружности, вписанной в треугольник 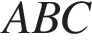 .
.
2. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен  . Найдите радиус вписанной окружности треугольника ABC.
. Найдите радиус вписанной окружности треугольника ABC.
3. Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
4. Три окружности с центрами 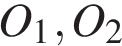 и
и 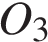 и радиусами 2,5, 0,5 и 4,5 соответственно попарно касаются внешним образом. Найдите угол
и радиусами 2,5, 0,5 и 4,5 соответственно попарно касаются внешним образом. Найдите угол 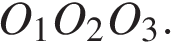
5. Две окружности с центрами 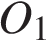 и
и 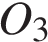 и радиусами 4,5 и 2,5 касаются друг с другом внешним образом и внутренним образом касаются окружности с центром
и радиусами 4,5 и 2,5 касаются друг с другом внешним образом и внутренним образом касаются окружности с центром 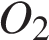 радиусом 7,5. Найдите угол
радиусом 7,5. Найдите угол 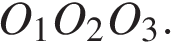
6. Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трёх окружностей.
7. В треугольнике 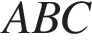 угол
угол 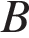 равен 120°, а длина стороны
равен 120°, а длина стороны 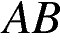 на
на 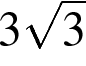 меньше полупериметра треугольника. Найдите радиус окружности, касающейся стороны
меньше полупериметра треугольника. Найдите радиус окружности, касающейся стороны 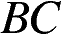 и продолжений сторон
и продолжений сторон 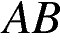 и
и 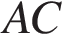 .
.
8. В треугольнике 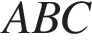 биссектриса угла
биссектриса угла 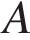 делит высоту, проведённую из вершины
делит высоту, проведённую из вершины 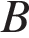 , в отношении
, в отношении  , считая от точки
, считая от точки 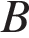 . Найдите радиус окружности, описанной около треугольника
. Найдите радиус окружности, описанной около треугольника 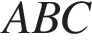 , если .
, если .
9. Две касающиеся внешним образом в точке K окружности, радиусы которых равны 16 и 48, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
10. Окружность радиуса 4 касается внешним образом второй окружности в точке 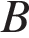 . Общая касательная к этим окружностям, проходящая через точку
. Общая касательная к этим окружностям, проходящая через точку 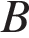 , пересекается с некоторой другой их общей касательной в точке
, пересекается с некоторой другой их общей касательной в точке 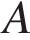 . Найдите радиус второй окружности, если
. Найдите радиус второй окружности, если  .
.
11. В окружности с центром в точке  проведены две хорды
проведены две хорды 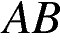 и
и  . Прямые
. Прямые 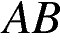 и
и  перпендикулярны и пересекаются в точке
перпендикулярны и пересекаются в точке  , лежащей вне окружности. При этом . Найдите
, лежащей вне окружности. При этом . Найдите  .
.
12. В прямоугольном треугольнике 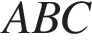 катет
катет 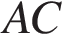 равен 8, катет
равен 8, катет 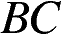 равен 15. Найдите радиус окружности, которая проходит через концы гипотенузы треугольника и касается прямой
равен 15. Найдите радиус окружности, которая проходит через концы гипотенузы треугольника и касается прямой 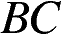 .
.
13. Окружности радиусов 14 и 35 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
14. Точки  и
и  лежат на стороне
лежат на стороне 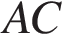 треугольника
треугольника 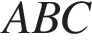 на расстояниях соответственно 9 и 11 от вершины
на расстояниях соответственно 9 и 11 от вершины  Найдите радиус окружности, проходящей через точки
Найдите радиус окружности, проходящей через точки  и
и  и касающейся луча
и касающейся луча  если
если
15. В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB = 20.


 Получите свидетельство
Получите свидетельство Вход
Вход











 Материал по математике по теме "Окружности" (55.25 КB)
Материал по математике по теме "Окружности" (55.25 КB)
 0
0 689
689 45
45 Нравится
0
Нравится
0




