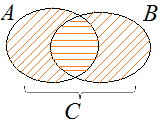
Пересечением двух множеств, называется третье множество, сформированное из элементов, которые входят в оба первых множества.
Например, если в одно множество входят числа от 1 до 10, а во второе — от 5 до 20, то пересечением этих множеств будут числа от 5 до 10, так как они входят в оба.
Пересечение множеств записывается так:
A ∩ B = {x | x ∈ A и x ∈ B}
На диаграмме Эйлера-Венна пересечение множеств обозначается общей частью кругов.
Множества могут не пересекаться вообще, одно может полностью включать другое.
Пересечение множеств может использоваться тогда, когда надо найти элементы, которые удовлетворяют нескольким условиям.
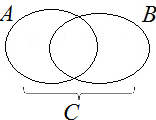
Объединением двух множеств, называется третье множество, сформированное из всех элементов обоих первых множеств. При этом если элемент входит в оба множества, то в объединенное он входит один раз. Это и понятно, так как множество по определению включает только разные элементы.
Например, объединением множества натуральных чисел от 1 до 10 и множества натуральных от 5 до 15 будет множество натуральных чисел от 1 до 15.
Объединение множеств описывается так:
A ∪ B = {x | x ∈ A или x ∈ B}
На диаграмме Эйлера-Венна объединение множеств обозначается всей областью кругов.
Разностью двух множеств, называют третье множество, в которое входят все элементы одного из двух множеств и не входят элементы принадлежащие обоим множествам.
Если результат пересечения и объединения двух множеств не меняется от перестановки множеств при выполнении операции, то результат разности зависит от того, какое множество из какого «вычитают».
Сравните. Даны множества A = {1,2,3,4,5} и B = {4,5,8,9}. Разность множеств обозначается знаком.
A B = {1,2,3}, т. к. 4 и 5 входят в множество B.

В то время как B A = {8,9}.
Понятно, что если у множеств нет общих элементов, то их разность будет равна «уменьшаемому», т. е. первому множеству. Если же множества полностью совпадают, то их разностью будет пустое множество.
Если все элементы «вычитаемого» множества B входят в состав «уменьшаемого» A (A B), то B называют дополнением некого множества C до A.
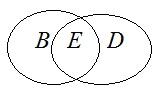
Пример: В классе 19 учеников: 10 девочек, 9 мальчиков.
10 девочек – это множество.
9 мальчиков – это множество.
Класс из 19 учеников – это множество С, которое объединяет два множества.
Пусть в классе 5 отличников – это множество D.
Из них 2 мальчика – это множество E.
Из какие элементов состоит множество Е?
Мальчики входят в множества В, так как 2 мальчика – отличники, они входят в множество D.
Множество Е есть пересечение двух множеств В и D(рис. 1).
Определение понятия объединение множеств.
Определение: объединением множеств А и В называется новое множество, состоящее из тех и только тех элементов, которые входят хотя бы в одно из множеств А или В (рис. 3).
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



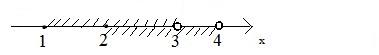









 Материал по математике "Пересечение и объединение множеств" (0.11 MB)
Материал по математике "Пересечение и объединение множеств" (0.11 MB)
 0
0 1537
1537 40
40 Нравится
0
Нравится
0


